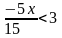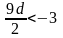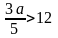§1.3.2 Линейные неравенства

Свойства числовых неравенств позволяют руководствоваться при решении неравенств следующими правилами:

Правило 1. Любой член неравенства можно перенести из одной части

неравенства в другую с противоположным знаком, не изменив при этом знак неравенства.

Правило 2. Обе части неравенства можно умножить или разделить на одно

и то же положительное число, не изменив при этом знак неравенства.

Правило 3. Обе части неравенства можно умножить или разделить на одно

и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Пример 1. Решить неравенство Зх - 5 > 7х - 15.

Решение. Перенесем член 7х в левую часть неравенства, а член - 5 — в правую часть неравенства, не забыв при этом изменить знаки и у члена 7х, и у члена - 5 (руководствуемся правилом 1). Тогда получим Зх - 7х > - 15 + 5, т. е. - 4х > - 10.

Разделим обе части последнего неравенства на одно и то же отрицательное число - 4, не забыв при этом перейти к неравенству противоположного смысла (руководствуясь правилом 3).

Получим х < 2,5. Это и есть решение заданного неравенства.

О т в е т: х < 2,5, или (-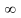 ; 2,5].

Пример 2. Решить неравенство

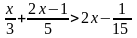
Решение. Умножим обе части неравенства на положительное число 15, оставив знак неравенства без изменения (правило 2). Это позволит нам освободиться от знаменателей, т. е. перейти к более простому неравенству, равносильному данному:

5х + 3(2х-1)>30х-1;

5х + 6х - 3 > 30х - 1;

11х-3>30х-1.

Воспользовавшись для последнего неравенства правилом 1, получим равносильное ему более простое неравенство:

11х - 30х > - 1 + 3, т. е.

-17х>2.

Наконец, применив правило 3, получим

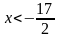
Ответ:

Задания по вариантам

№ варианта	Решить неравенство:
1	2а-11 >а + 13; 10х + 9 > - 3(2 - 5х);
2	8b + 3 < 9b - 2; 2(3 – 2z)+ 3(2-z) < 40;
3	6-4с>7-6с; 2(х + 1) – 1< 7 +8x
4	3-2х< 12 -5х. – 2(4z + 1) < 3 – 10z;
5	d-5>3-d; 8 + 6р < 2(5р - 8);
6	3m + 17<m-13; 3(2-4n)>6-3n
7	р + 4>12 + 9р. –(6y+2)>6(y-1)
8	-2x + 12>3x-3; 7-16r>-2(8r-1)+5
9	3t+5>7t-7 4(а + 1) + За > 7а + 2;
10	6y+8>10y-8 2(6y+2)<3(y-1)

§1.4.Построение графиков квадратичной функции

Определение: Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где х - независимая переменная, a, b и с -некоторые числа (причём а≠0).

Определение: Графиком квадратичной функции является парабола, ветви которой направлены вверх (если а>0) или вниз (если а<0).

§1.4.1 Построение графика функции y=ax²+bx+c

1. Описать функцию: название функции, что является графиком функции, куда направлены ветви параболы.

2. Найти координаты вершины параболы А(m;n) по формулам: 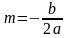, 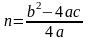; или n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение. Прямая x=m является осью симметрии параболы"

3. Заполнить таблицу значений функции, в ней расположить вершину в середине таблицы и взять соседние симметричные значения х (посчитать значение функции в выбранных значениях х)

4. Построить график функции: отметить в координатной плоскости точки, координаты которых указаны в таблице; соединить их плавной линией.

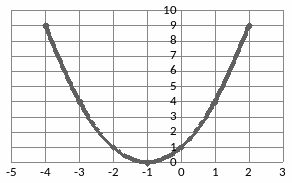
Пример 1: Построить график функции y=x²+2x+1

1. Квадратичная функция, графиком является парабола, ветви которой направленны вверх;

2. Нахождение вершины А(m;n)

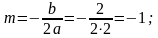
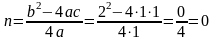
A(-1;0)

3. Таблица значений

   х	-4	-3	-2	-1	0	1	2
   у	9	4	1	0	1	4	9

4. График