
- •Лекция 01: Вводные замечания Основные понятия, принципы и ограничения реляционных баз данных Основные определения
- •Принципы, реализуемые реляционными субд
- •Ограничения реляционных баз данных
- •Реляционная судб ms sql Server
- •Ms sql Server как система управления обработкой транзакций
- •Ms sql Server как система поддержки принятия решений
- •Службы ms sql Server Серверная часть системы
- •Клиентская часть системы
- •Лекция 02: Что делают и за что отвечают администраторы баз данных Microsoft sql Server
- •Инсталляция и конфигурирование
- •Инсталляция программного обеспечения
- •Конфигурирование аппаратуры и программного обеспечения
- •Безопасность
- •Аудит системы
- •Обычная работа
- •Резервное копирование и восстановление
- •Управление пользователями
- •Прочая обычная работа
- •Уровень качества обслуживания
- •Мониторинг и настройки производительности
- •Состав системы и планирование мощности
- •Обеспечение периодов работоспособности системы
- •Планирование периодов неработоспособности
- •Восстановление после аварий
- •Документирование
- •Документация о конфигурации
- •Системный журнал
- •Документация о структуре системы
- •Планы обычного технического обслуживания
- •Планы восстановления после аварий
- •Проектирование и разработка
- •Создание модели данных и анализ
- •Проектирование базы данных
- •Разработка хранимых процедур
- •Разработка приложений
- •Информационная помощь другим сотрудникам
- •Прочие обязанности администратора баз данных
- •Администрирование кластера
- •Работа в службе технических консультаций для пользователей
- •Оценка закупаемого оборудования и программного обеспечения
- •Слежение за мощностью системы
- •Типы данных
- •Значение null
- •Правила порождения идентификаторов
- •Системные таблицы
- •Временные таблицы
- •Пользовательские таблицы
- •Физическая архитектура баз данных
- •Страницы и группы страниц
- •Файлы и группы файлов
- •Лекция 04: Основы программирования в ms sql Server Реляционная алгебра
- •Операции реляционной алгебры
- •Реализация операций реляционной алгебры в языке sql
- •Описание синтаксиса языка Transact-sql Управляющие конструкции
- •Логические операторы
- •Лекция 05: Создание и использование умолчаний, ограничений и правил
- •Умолчания
- •Определение и модифицирование умолчаний с помощью t-sql
- •Оператор create table с атрибутом default
- •Оператор alter table с атрибутом default
- •Оператор create default и процедура sp_bindefault
- •Процедура sp_unbindefault
- •Ограничения
- •Создание и модифицирование ограничений с помощью t-sql Ограничение not null
- •Ограничение unique
- •Ограничение primary key
- •Ограничение foreign key
- •Ограничение check
- •Правила
- •Создание Rule-объекта с помощью t-sql
- •Лекция 06: Создание и использование индексов Что такое индекс?
- •Понятия индексирования
- •Индексные ключи
- •Простые индексы
- •Составные индексы
- •Уникальность индекса
- •Уникальный индекс
- •Неуникальные индексы
- •Типы индексов
- •Кластеризованные индексы
- •Некластеризованные индексы
- •Полнотекстовые индексы
- •Использование коэффициента заполнения для предупреждения расщеплений страниц
- •Создание индексов
- •Использование Management Studio
- •Категория «Общие»
- •Категория «Идентификация»
- •Категория «Конструктор таблиц»
- •Спецификация пространства данных
- •Характеристики заполнения
- •Использование t-sql
- •Лекция 07: Программируемые объекты в ms sql Server Пользовательские функции sql Server
- •Функции Scalar
- •Функции Inline
- •Функции Multistatement
- •Изменение функций
- •Удаление функций
- •Использование sql Server Management Studio
- •Хранимые процедуры
- •Примеры использования хранимых процедур
- •Лекция 08: Другие программируемые объекты ms sql Server Определение триггера в стандарте языка sql
- •Реализация триггеров в среде ms sql Server
- •Примеры использования триггеров
- •Курсоры
- •Запрос курсора
- •Обработка курсоров
- •Преимущества использования курсоров
- •Курсоры базовой таблицы
- •Статические курсоры
- •Последовательные курсоры
- •Последовательные курсоры «только для чтения»
- •Курсоры, управляемые набором ключей
- •Работа с объединениями
- •Правила выбора типа курсора
- •Получение блокировок
- •Неявное преобразование типа курсора
- •Лекция 09: Проектирование системы Microsoft sql Server
- •Системные требования
- •Системное приложение
- •Oltp (системы оперативной обработки транзакций)
- •Dss (системы поддержки принятия решений)
- •Системы пакетной обработки данных
- •Требования
- •Требования к уровню обслуживания
- •Производительность
- •Мощность
- •Обеспечение работоспособности
- •Размещение базы данных
- •Журнал транзакций
- •Файлы данных
- •Приложение
- •Архитектура
- •Производительность и масштабируемость
- •Проектирование системы безопасности
- •Уровни системы безопасности Система безопасности уровня сервера
- •Система безопасности уровня базы данных
- •Права собственности на объект
- •Лекция 10: Microsoft sql Server и Microsoft Cluster Services Разновидности отказов
- •Обзор mscs
- •Основные понятия
- •Компоненты кластера
- •Программное обеспечение mscs для управления кластером
- •Взаимосвязь между серверами
- •Разделяемая дисковая система
- •Подсистемы ввода-вывода
- •Внутренняя raid-система
- •Внешняя raid-система
- •Категории приложений, работающих с кластерами
- •Режимы mscs
- •Активно-пассивные кластеры
- •Активно-активные кластеры
- •Примеры кластеризованных систем
- •Пример 1 – система с высокой готовностью со статическим балансированием нагрузки
- •Пример 2 – система с «горячим резервированием» с максимальной готовностью
- •Пример 3 – кластеризация части сервера
- •Пример 4 – только виртуальные серверы, без переходов по отказам
- •Конфигурирование sql Server для работы на кластере
- •Планирование конфигурации
- •Задание времени восстановления
- •Конфигурирование sql Server для активно-пассивных кластеров
- •Конфигурирование sql Server для активно-активных кластеров
- •Лекция 11: Транзакции и блокировка транзакций
- •Что такое транзакция?
- •Acid-свойства
- •Атомарность
- •Согласованность
- •Изолированность
- •Поведение параллельных транзакций
- •Задание уровня изолированности
- •Устойчивость
- •Режимы транзакций
- •Режим автофиксации
- •Явный режим
- •Фиксирование транзакций
- •Создание вложенных транзакций
- •Неявный режим
- •Откаты транзакций
- •Автоматические откаты
- •Программируемые откаты
- •Точки сохранения
- •Блокировка транзакций
- •Возможности управления блокировками
- •Уровни блокировок
- •Режимы блокировки
- •Разделяемая блокировка
- •Блокировка изменений
- •Монопольная блокировка
- •Блокировка намерения
- •Блокировка схемы
- •Блокировка массовых изменений
- •Блокирование и взаимоблокировки
- •Лекция 12: Управление пользователями и системой безопасности
- •Разрешение удалённого доступа
- •Разрешение удалённых соединений
- •Обеспечение безопасности внешнего доступа
- •Управление доступом к экземплярам sql Server
- •Выбор режима проверки подлинности
- •Настройка режима проверки подлинности
- •Соединение с экземпляром sql Server
- •Предоставление доступа пользователям и группам Windows
- •Предоставление доступа именам входа sql Server
- •Принудительное применение политики паролей
- •Управление разрешениями для экземпляра
- •Получение информации о принадлежности к серверной роли
- •Запрет доступа пользователям
- •Рекомендации по управлению доступом
- •Применение схем и ролей. Общие принципы
- •Управление доступом в службах отчётов
- •Управление доступом в службах уведомлений
- •Управление доступом в интеграционных службах
- •Управление доступом в службах репликации
- •Управление доступом для sql Server Agent
- •Управление доступом для Database Mail
- •Управление доступом к базе данных с помощью протокола http
- •Лекция 13: Репликации
- •Что такое репликация базы данных?
- •Понятия репликации Компоненты репликации
- •Издатели
- •Дистрибьюторы
- •Подписчики
- •Типы репликации
- •Репликация моментальных снимков
- •Репликация транзакций
- •Репликация слиянием
- •Данные репликации
- •Публикации
- •Push-подписка и pull-подписка
- •Push-подписка (принудительная)
- •Pull-подписка (по запросу)
- •Агенты репликации
- •Snapshot Agent (Агент создания снимков состояния)
- •Репликация слиянием
- •Репликация моментальных снимков
- •Лекция 14: Средства автоматического администрирования
- •Средства автоматического конфигурирования sql Server
- •Динамическое управление памятью
- •Как действует динамическое управление памятью
- •Пул памяти
- •Параметры конфигурирования памяти sql Server
- •Другие параметры динамического конфигурирования
- •Параметр locks (блокировки)
- •Параметр recovery interval (интервал восстановления)
- •Параметр user connections (количество соединений с пользователями)
- •Статистика
- •Команда create statistics
- •Процедура sp_createstats
- •Команда update statistics
- •Процедура sp_autostats
- •Контрольные точки
- •Планы обслуживания баз данных
- •Использование мастера для создания плана обслуживания
- •Лекция 15: Автоматизация административных задач с помощью службы sqlServerAgent
- •Задания
- •Создание задания в Management Studio
- •Использование t-sql
- •Просмотр журнала выполнения задания
- •Использование Management Studio
- •Использование t-sql
- •Предупреждения
- •Протоколирование сообщений в журнале событий
- •Создание предупреждения о событии sql Server
- •Создание предупреждения о производительности sql Server
- •Операторы
- •Лекция 16: Резервное копирование Microsoft sql Server
- •Воспроизведение
- •Отказы системы
- •Отказы оборудования
- •Отказы программного обеспечения
- •Человеческие ошибки
- •Журнальное протоколирование в sql Server Журнал транзакций
- •Поток откладываемой записи
- •Последовательная запись в журнал
- •Размер журнала транзакций
- •Воспроизведение с помощью журнала транзакций
- •Свойства журнала транзакций
- •Непротоколируемые операции
- •Bulk copy и программа bcp
- •Текстовые операции
- •Контрольные точки
- •Операции контрольной точки
- •Конфигурирование интервала между контрольными точками
- •Методы резервного копирования
- •Полное резервное копирование
- •Разностное резервное копирование
- •Резервное копирование журнала транзакций
- •Резервное копирование группы файлов
- •Резервное копирование файла данных
- •Комбинирование разностных резервных копий и резервных копий журнала транзакций
- •Выполнение резервного копирования
- •Создание логических устройств резервного копирования
- •Создание устройств резервного копирования с помощью t-sql
- •Создание удалённого устройства резервного копирования
- •Резервное копирование с помощью Management Studio
- •Лекция 17: Полная модель восстановления
- •Модель восстановления с неполным протоколированием
- •Восстановление базы данных из резервных копий
- •Извлечение информации резервного копирования
- •Восстановление базы данных через интерфейс среды sql Server Management Studio
- •Восстановление базы данных при простой стратегии резервного копирования с использованием t-sql
- •Восстановление базы данных при полной стратегии резервного копирования с использованием t-sql
- •Восстановление системных баз данных
- •Восстановление базы данных master
- •Восстановление баз данных msdb и model
Лекция 04: Основы программирования в ms sql Server Реляционная алгебра
В основе реляционной алгебры лежит следующая идея: так как отношение – это множество кортежей, то и средства манипулирования отношениями должны быть такими же, как традиционные теоретико-множественные операции, дополненные специфическими для баз данных операциями.
Операции реляционной алгебры
Расширенный начальный вариант алгебры, определённый Коддом, состоит из восьми алгебраических операций, которые делятся на два класса – теоретико-множественные операции и специальные реляционные операции.
В состав теоретико-множественных операций входят:
объединение отношений;
пересечение отношений;
взятие разности отношений;
декартово произведение отношений.
Специальные реляционные операции включают:
выборку или ограничение отношения;
проекцию отношения;
соединение отношений;
деление отношений.
Приведём общую интерпретацию этих реляционных операций:
объединение: возвращает отношение, содержащее все кортежи, которые принадлежат либо одному, либо обоим из заданных отношений;
Объединением двух совместимых по типу отношений А и В (А union В) называется отношение с тем же заголовком, как и в отношениях А и В, и с телом, состоящим из множества всех кортежей t, принадлежащих А или В, или обоим отношениям за исключением повторяющихся (рис. 4.1).

рис 4.1. Пример реализации операции объединения
пересечение: возвращает отношение, содержащее кортежи, которые принадлежат одновременно двум заданным отношениям;
Пересечением двух совместимых по типу отношений A и B (A intersect B) называется отношение с тем же заголовком, как и в отношениях A и B, и с телом, состоящим из множества кортежей t, принадлежащих одновременно обоим отношениям A и B (рис. 4.2).

рис 4.2. Пример реализации операции пересечения
разность: возвращает отношение, содержащее все кортежи, которые принадлежат первому из двух заданных отношений и не принадлежат второму;
Разность двух совместимых по типу отношений A и B (A minus B) – это отношение с тем же заголовком, как и в отношениях A и B, и с телом, состоящим из множества всех кортежей t, принадлежащих отношению A и не принадлежащих отношению B (Рис.4.3).

рис 4.3. Пример реализации операции разность
декартово произведение: возвращает отношение, содержащее все возможные кортежи, которые являются сочетанием двух кортежей, принадлежащих соответственно двум заданным отношениям (Рис.4.4);

рис 4.4. Пример реализации операции декартово произведение
выборка: возвращает отношение, содержащее кортежи из заданного отношения, которые удовлетворяют указанным условиям;
Выборка
– это сокращённое название
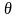 -выборки,
где
обозначает любой скалярный оператор
сравнения (=, <>, >, >= и т.д.).
-выборкой
из отношения А по атрибутам X и Y (в этом
порядке)
-выборки,
где
обозначает любой скалярный оператор
сравнения (=, <>, >, >= и т.д.).
-выборкой
из отношения А по атрибутам X и Y (в этом
порядке)
А where X θ Y
называется отношение, имеющее тот же заголовок, что и отношение А, и тело, содержащее множество всех кортежей t отношения А, для которых проверка условия «X Y» даёт значение истина. Атрибуты X и Y должны быть определены на одном домене, а оператор должен быть определён в этом домене (Рис. 4.5).

рис 4.5. Пример реализации операции выборка
Выборка, как было определено, допускает простые сравнения в выражении where. Однако на основании свойства замкнутости можно однозначно расширить определение до формы, в которой условие в выражении where будет содержать произвольное число логических сочетаний таких простых сравнений (с использованием логических связок AND, OR, NOT и круглых скобок).
проекция: возвращает отношение, содержащее все кортежи заданного отношения, которые остались в этом отношении после исключения из него некоторых атрибутов;
Результатом
проекции отношения A по списку атрибутов
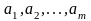 является отношение, с заголовком,
определяемым множеством атрибутов
и с телом, состоящим из кортежей вида
является отношение, с заголовком,
определяемым множеством атрибутов
и с телом, состоящим из кортежей вида
 таких, что в отношении A имеется кортеж,
атрибут
таких, что в отношении A имеется кортеж,
атрибут
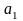 которого имеет значение
которого имеет значение
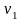 ,
атрибут
,
атрибут
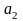 имеет значение
имеет значение
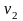 ,
..., атрибут
,
..., атрибут
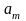 имеет значение
имеет значение
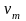 .
Тем самым, при выполнении операции
проекции получается «вертикальное»
подмножество отношения-операнда, т.е.
подмножество, получаемое исключением
всех атрибутов, не указанных в списке
атрибутов, с последующим уничтожением
кортежей-дубликатов из того, что осталось
(рис.4.6).
.
Тем самым, при выполнении операции
проекции получается «вертикальное»
подмножество отношения-операнда, т.е.
подмножество, получаемое исключением
всех атрибутов, не указанных в списке
атрибутов, с последующим уничтожением
кортежей-дубликатов из того, что осталось
(рис.4.6).

рис 4.6. Пример реализации операции прекция
соединение возвращает отношение, кортежи которого – это сочетания двух кортежей (принадлежащих соответственно двум различным отношениям), имеющих общее значение для одного или нескольких общих атрибутов этих двух отношений (и такие общие значения в результирующем кортеже появляются только один раз;
Результат этой операции можно рассматривать как суперпозицию операций декартово произведение и выборки (ограничения) с указанным предикатом (условием соединения) (Рис.4.7).

рис 4.7. Пример реализации операции соединение
деление для двух отношений, бинарного и унарного, возвращает отношение, содержащее все значения одного атрибута бинарного отношения, которые соответствуют (в другом атрибуте) всем значениям в унарном отношении (Рис. 4.8).

рис 4.8. Пример реализации операции деление
Кроме того, в состав алгебры включается операция присваивания, позволяющая сохранить в базе данных результаты вычисления алгебраических выражений, и операция переименования атрибутов, дающая возможность корректно сформировать заголовок (схему) результирующего отношения:
операция переименования производит отношение, тело которого совпадает с телом операнда, но имена атрибутов изменены.
операция присваивания позволяет сохранить результат вычисления реляционного выражения в существующем отношении БД.
Поскольку результатом любой реляционной операции (кроме операции присваивания) является некоторое отношение, можно образовывать реляционные выражения, в которых вместо отношения – операнда некоторой реляционной операции находится вложенное реляционное выражение.
Для алгебры, у которой операции замкнуты относительно понятия отношения, каждая операция должна производить отношение с двумя составляющими: телом и заголовком. Только в этом случае будет действительно возможно строить вложенные выражения. Операции объединения, пересечения разности требуют от отношений-операндов совместимых по типу. Два отношения называются совместимыми по типу, если каждое из них имеет одинаковое множество имён атрибутов и если соответствующие атрибуты определены на одном и том же домене. Если необходимо выполнить операцию объединения, пересечения или вычитания двух отношений, которые почти совместимы по типу, за исключением некоторых различий в именах атрибутов, можно использовать оператор переименования, чтобы сделать эти отношения полностью совместимыми по типу, прежде чем выполнить необходимую операцию.
