
- •Электроника и микропроцессорная техника
- •1.Элементы математического аппарата цифровой техники
- •1.1.Системы счисления
- •1.2.Двоичная арифметика
- •1.3.Числовые коды
- •1.4.Алгебра логика
- •1.4.1.Аксиомы алгебры логики
- •1.4.2.Теоремы и тождества алгебры логики
- •1.5.Логические функции
- •1.5.1.Область определения логических функций
- •1.5.2.Таблица истинности
- •1.5.3.Логические функции одной переменной
- •1.5.4.Логические функции двух переменных
- •1.5.5.Теоремы разложения
- •1.6.Представление логической функции в виде сднф и скнф
- •1.6.1.Первичные термы
- •1.6.2.Минтермы и макстермы
- •1.6.3.Запись функции в виде сднф и скнф
- •1.6.4.Совершенные нормальные формы в базисах и-не и или-не
- •1.7.Минимизация логических функций
- •1.7.1.Конъюнктивные и дизъюнктивные термы
- •1.7.2.Правила минимизации логических функций
- •1.7.3.Минимизация функции с помощью карты Карно
- •2.7.2.Логические элементы с открытым коллектором
- •2.7.3.Логические элементы с открытым эмиттером
- •2.7.4.Логические элементы с третьим состоянием выходов
- •2.7.5.Применение лэ с открытым коллектором
- •3.2.Модели потенциальных схем (автоматов)
- •3.2.1.Основная модель асинхронного потенциального автомата
- •3.2.2.Основная модель синхронного автомата
- •3.2.3.Синтез асинхронных потенциальных триггеров и элементов памяти
- •3.2.4.Синтез синхронных триггеров
1.5.1.Область определения логических функций
Областью определения функции n
переменных xn-1,…,x0
является совокупность точек
n-мерного пространства,
причем каждая из точек задается
определенной комбинацией значений этих
переменных
![]() где ep
=0 или 1, (p=0,1,2,…,n-1).
где ep
=0 или 1, (p=0,1,2,…,n-1).
Например – пусть есть некая функция 4х переменных n=4 то одна из точек определения этой функции Vi =(en-1…ep…e0) где i=en-1…ep…e0 (например, Vi=1100).
Из этих соотношений видно, что точки
определения можно посчитать по порядку
от
0 до 2n
как в двоичном счете, так и десятичном
и в любом другом. Поэтому область
определения функции f(v)
n переменных имеет
2n точек т.е.
![]()
Для задания функции f(v)
следует указать ее значения во всех
точках области определения т.е. следует
задать значения f(vi)=0
или 1 где i=0,1,2,…,2n-1.
В совокупности эти значения представляют
некое двоичное число из 2n
разрядов т.к. имеется всего
![]() различных 2n
разрядных двоичных чисел, то и число
различных функций n
переменных равно
.
различных 2n
разрядных двоичных чисел, то и число
различных функций n
переменных равно
.
Функции n переменных могут зависеть не от всех переменных xn-1…x0. Такие функции называются вырожденными.
Также функция может быть задана как во всех точках определения, так и не во всех:
функция n переменных f(v) называется полностью определенной, если ее значения f(vi)=0 или 1 заданы во всех 2n точках Vi области определения;
если же значение функции не задано хотя бы в одной точки Vi, то она называется не полностью определенной, это означает, что функция в этой точке может иметь значение 1 или 0 – и это не важно – такое значение будем называть коэффициентом с;
если значения функции не заданы во всех точках Vi, то она называется полностью неопределенной.
1.5.2.Таблица истинности
Так как область определения любой функции n переменных конечна 2n точек она может быть задана таблицей значений f(vi)=0 или 1 которые она принимает в точках vi, где i=0,1,…,2n-1. Такие таблицы называются таблицами истинности.
Например: функция 2х переменных
-
Vi точки определения функции
Значения точек определения функции (значения e1,e0 переменных функции x1,x0)
Значение функции f(v) в точках определения
V0
0 0
1
V1
0 1
0
V2
1 0
0
V3
1 1
0
1.5.3.Логические функции одной переменной
Разберем параметры таких функций:
n=1 – число переменных;
m=2 – число точек определения;
N=4 – число всех функций одной переменной.
Рассмотрим каждую функцию:
 –
нулевая функция.
–
нулевая функция.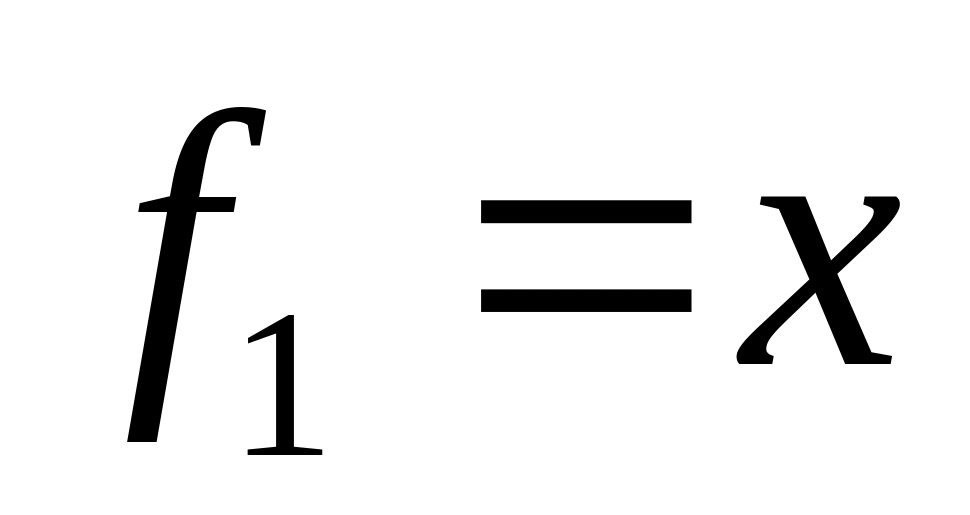 –
функция повторения.
–
функция повторения.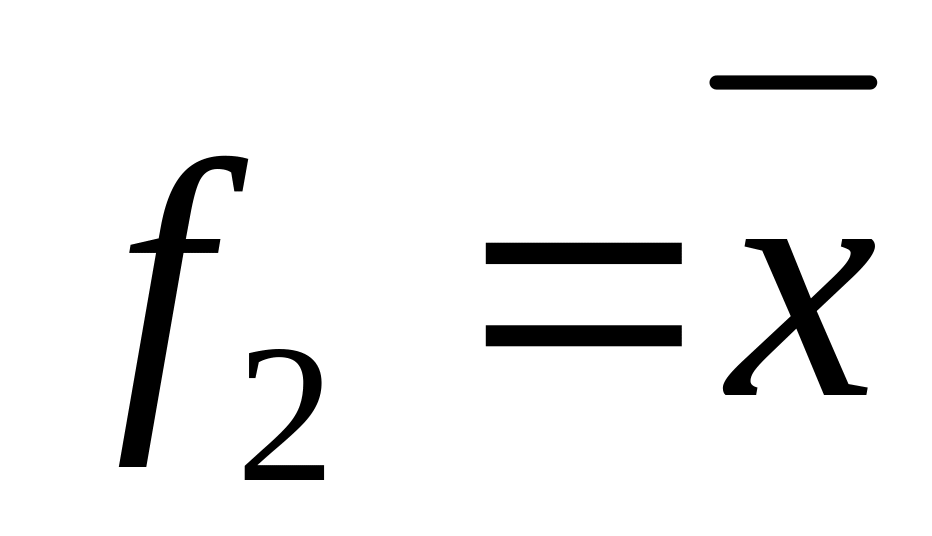 –
функция отрицания.
–
функция отрицания.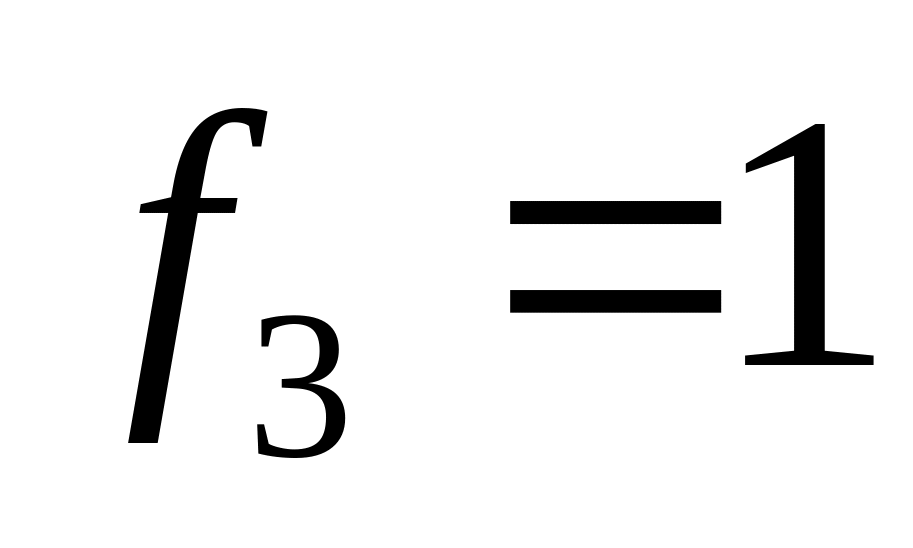 – единичная функция.
– единичная функция.
Таблица истинности функций одной переменной
-
Vi
x0
0
0
0
0
1
1
1
1
0
1
0
1
1.5.4.Логические функции двух переменных
Рассмотрим параметры функций:
n=2 – число переменных;
m=4 – число точек определения;
N=16 – число всех функций двух переменных.
Таблица истинности всех функций двух переменных
-
Vi
x1,x0
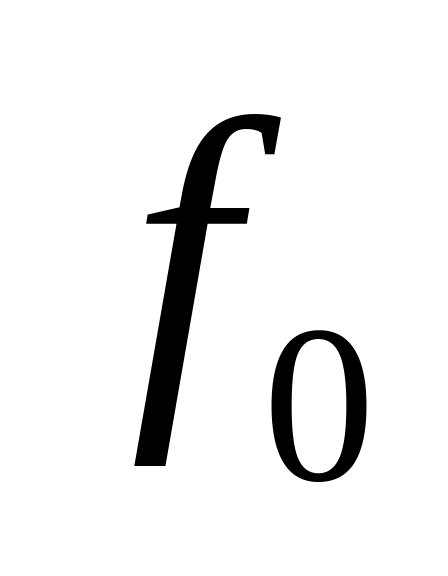
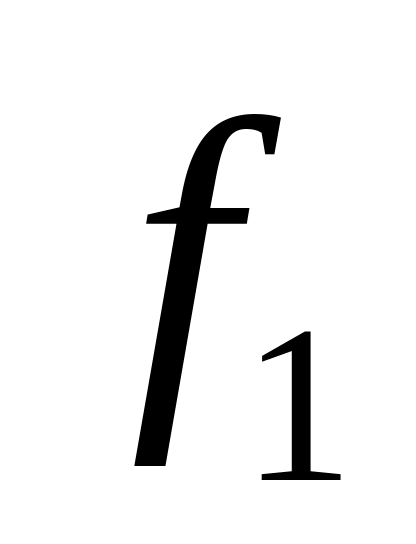
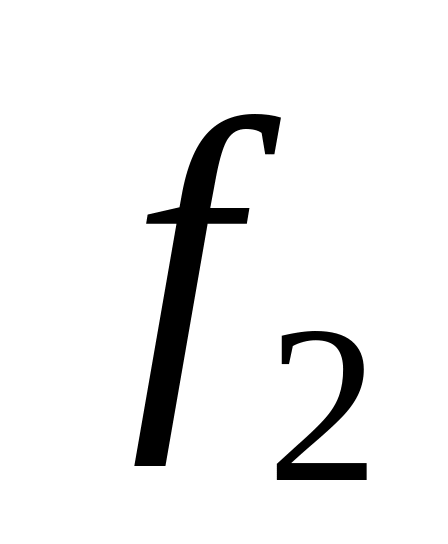
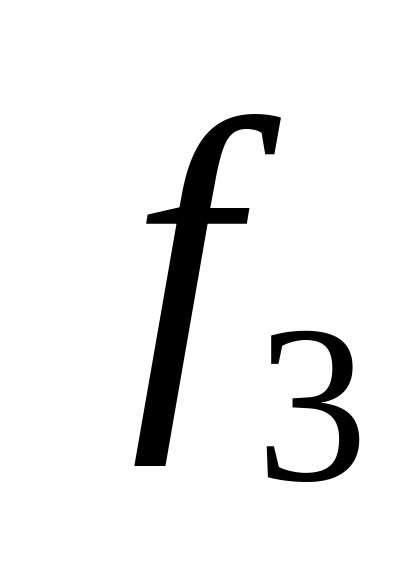
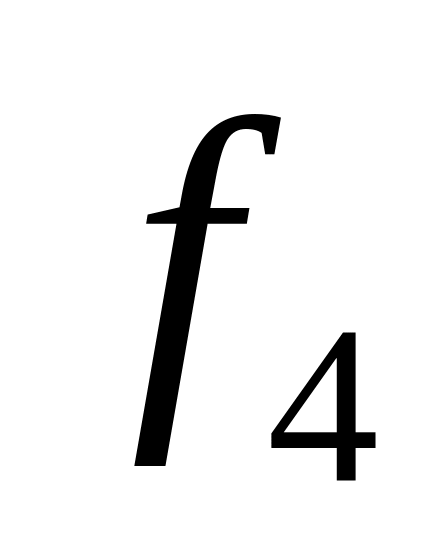
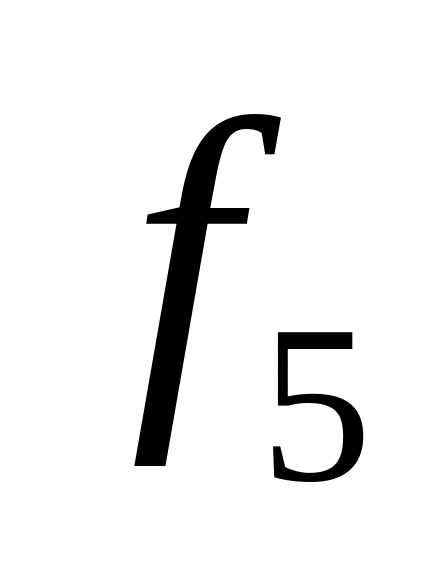
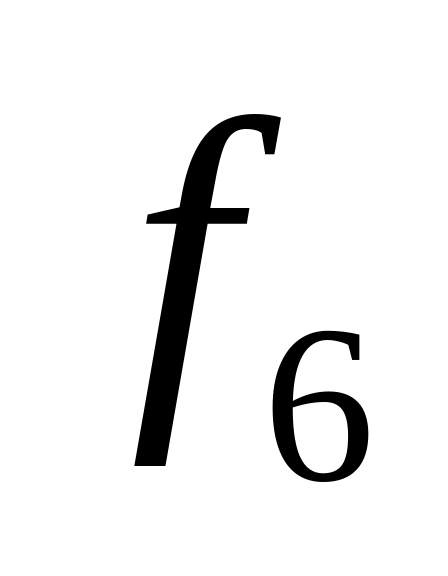
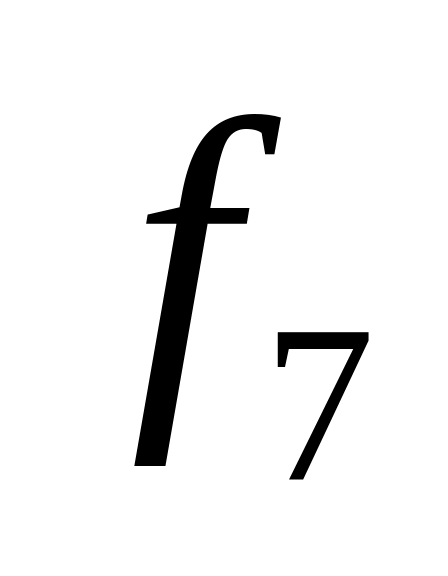
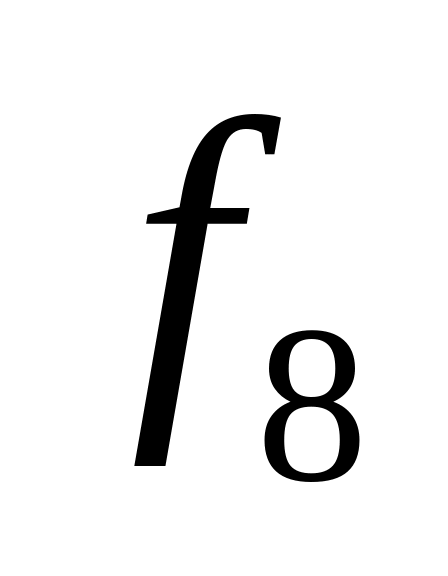

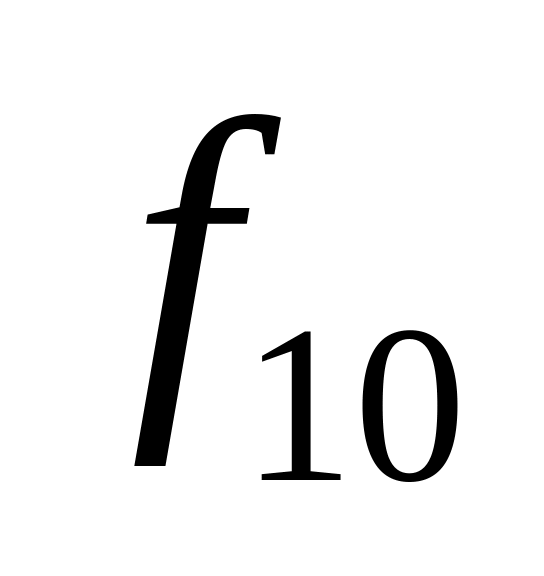
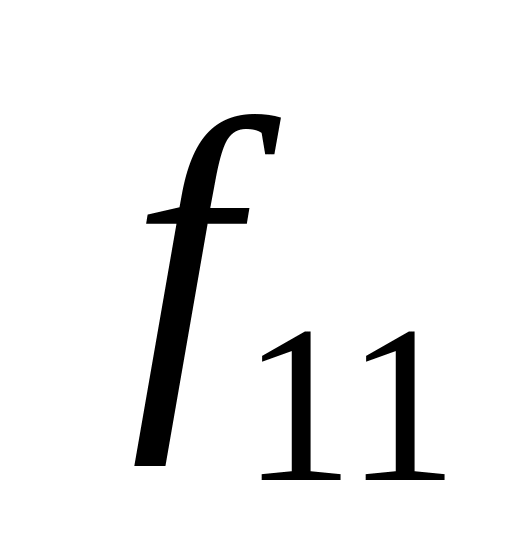
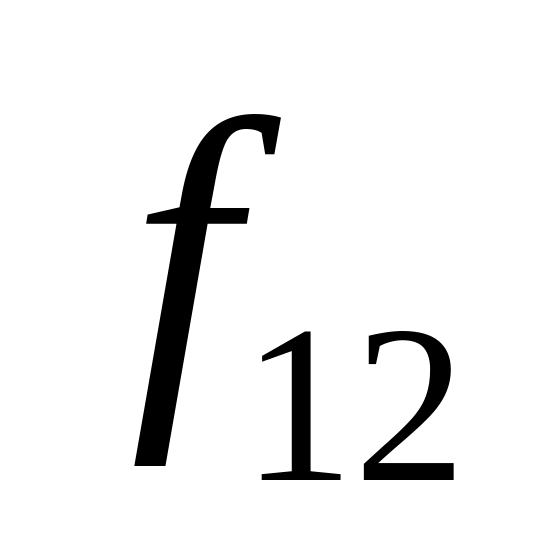
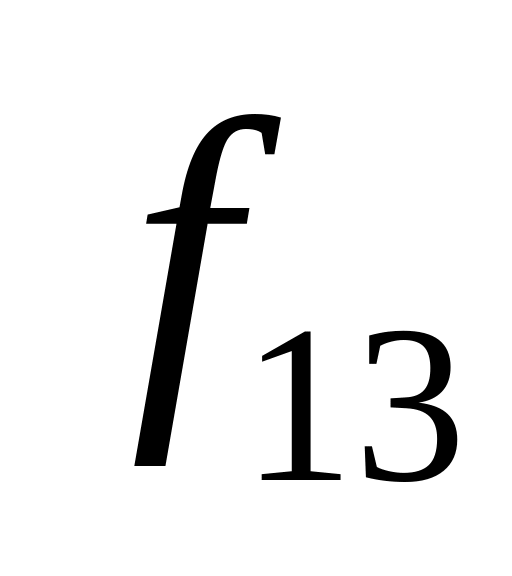
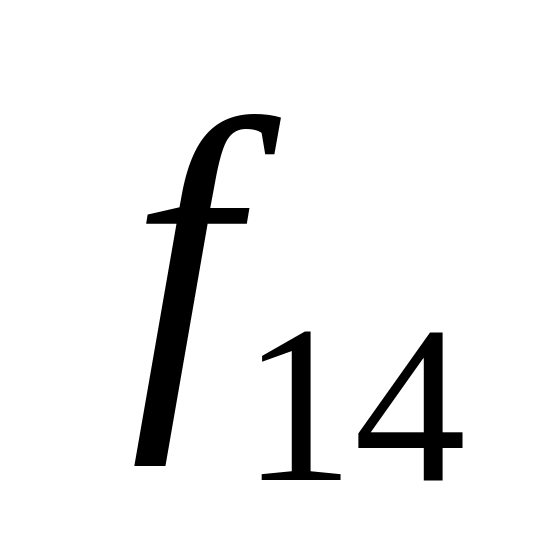
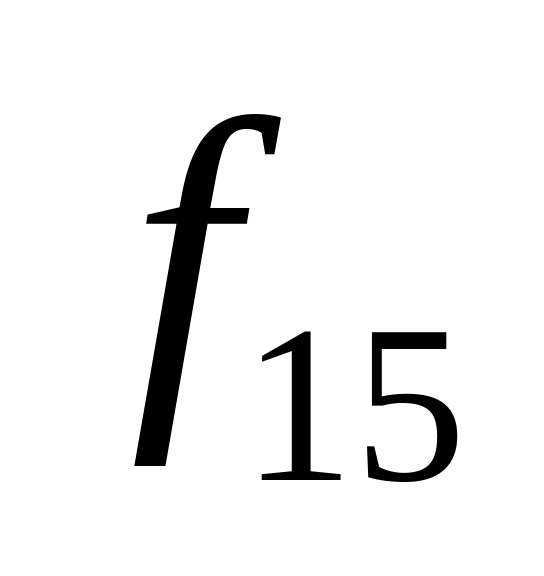
0
0 0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0 1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
2
1 0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
3
1 1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Значительный интерес представляют невырожденные функции, которые разберем подробно:
Функция логического умножения (конъюнкция).
![]() – логическое умножение, описывает
работу логического элемента И.
– логическое умножение, описывает
работу логического элемента И.
-
Vi
x1,x0

0
0 0
0
1
0 1
0
2
1 0
0
3
1 1
1
Функция логического сложения (дизъюнкция)
![]() – логическое сложение, описывает работу
логического элемента ИЛИ.
– логическое сложение, описывает работу
логического элемента ИЛИ.
-
Vi
x1,x0

0
0 0
0
1
0 1
1
2
1 0
1
3
1 1
1
Функция сложение по модулю два (исключающее ИЛИ, неравнозначность)
![]() – сложение по модулю два, применяется
для арифметического сложения
– сложение по модулю два, применяется
для арифметического сложения
-
Vi
x1,x0

0
0 0
0
1
0 1
1
2
1 0
1
3
1 1
0
Функция Пирса логическое сложение с отрицанием, отрицание дизъюнкции (стрелка Пирса ИЛИ-НЕ)
![]() – логическое сложение с отрицанием
ИЛИ-НЕ
– логическое сложение с отрицанием
ИЛИ-НЕ
-
Vi
x1,x0
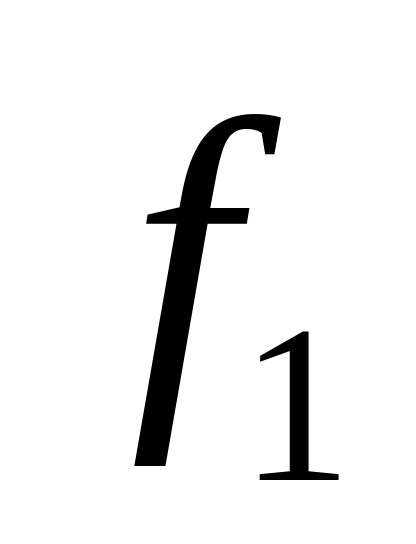

0
0 0
1
1
0 1
0
2
1 0
0
3
1 1
0
Функция Шеффера, отрицание от логического умножения (штрих Шеффера И-НЕ)
![]() – логическое умножение с отрицанием
И-НЕ
– логическое умножение с отрицанием
И-НЕ
-
Vi
x1,x0

0
0 0
1
1
0 1
1
2
1 0
1
3
1 1
0
Функции двух переменных исключительно важны в силу того, что любая логическая функция n переменных может быть получена из них методом суперпозиции – подстановкой этих функций в место переменных в другие функции.
