Перевод действительных чисел

Любое число N может быть единственным образом представлено в системе счисления с основанием р.

N = a_n pⁿ + a_n-1 p^n-1+ ... + a₀ p⁰ + a_-1 p^-1 + a_-2 p^-2 + ... + a_-m p^-m,

где a_i – цифры системы счисления; 0≤ a_i  p-1; a_n  0;

n и m – число целых и дробных разрядов, соответственно.

Перевод чисел в 10-чную систему счисления.

Для того чтобы перевести число в 10-чную систему счисления, необходимо составить сумму степенного ряда с основанием системы, в которой записано число, а затем найти значение этой суммы.

Пример. Перевести число 110110,01₂ в 10-чную систему.

5 4 3 2 1 0 1 2

110110,01₂ = 1*2⁵ + 1*2⁴ + 0*2³ + 1*2² + 1*2¹ + 0*2⁰ + 0*2^-1 + 1*2^-2 =

= 32 + 16 + 4 + 2 + 0,25 = 54,25₁₀

Пример. Перевести число A2F,4₁₆ в 10-чную систему.

2 1 0 1

A2F,4₁₆ = 10*16² + 2*16¹ + 15*16⁰+ 4*16^-1 = 2560 + 32 + 15 + 0,25 = 2607,25₁₀

Перевод чисел из 10-чной системы счисления.

1. Перевести целую часть в систему счисления с основанием р (метод деления уголком)

2. Перевести дробную часть в систему счисления с основанием р

При переводе правильной десятичной дроби в систему счисления с основанием р необходимо:

• сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на p, отделяя после каждого умножения целую часть произведения.

• Число в новой системе счисления записывается в виде целых частей произведения, начиная с первого.

• Умножение производится до тех пор, пока дробная часть пpоизведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Достаточно того количества цифр в результате, которое поместится в ячейку.

3. В ответе перед запятой следует записать целую часть, а после запятой – дробную часть.

Пример: Перевести число 0,532 из 10-тичной системы в двоичную с точностью до тысячных.

0 , 532

* 2

1, 064

* 2

0, 128

* 2

0, 256 Ответ: 0,532₁₀ = 0,100₂

Пример: Перевести число 0,974 из 10-тичной системы в 16-ричную с точностью до тысячных.

0, 974

* 16

15, 584

* 16

9, 344

* 16

5, 504 Ответ: 0,974₁₀ = 0,F95₁₆

Пример: Перевести число 0,1875 из 10-тичной системы в 8-ричную/

0 , 1875

* 8

1, 5000

* 8

4, 0000 Ответ: 0,1875 = 0,14₈

Если требуемая точность перевода числа N составляет k знаков после запятой, то предельная абсолютная погрешность при этом = p -(k+1) / 2.

Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Арифметические операции в позиционных системах счисления

Сложение и вычитание эффективно выполнять в исходной системе счисления. Способ с переводом каждого числа в 10-тичную систему, выполнении действия в ней, а затем обратного преобразования существенно длиннее и зачастую приводит к ошибкам.

При сложении чисел в произвольной позиционной системе счисления с основанием р в каждом разряде производится сложение цифр слагаемых и цифры, переносимой из соседнего младшего разряда, если она имеется. При этом необходимо учитывать, что если при сложении чисел получилось число, большее или равное р, то представляем его в виде p*k + b, где k N – количество единиц переноса в следующий разряд 0 ≤ b ≤ p - 1

При сложении и вычитании двоичных чисел достаточно знать правила сложения двоичных цифр (таблицу сложения двоичной системы):

0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10

Примеры:

1 1 1

1) 11001₂

+ 1101₂

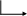
100110₂

1 +1 = 2 = 1*2 + 0 («1» переносится в старший разряд)

0 +0 + 1 = 1

0 + 1 = 1

1 + 1 = 2 = 1*2 + 0 («1» переносится в старший разряд)

1 + 0 + 1 = 2 = 1*2 + 0 («1» переносится в старший разряд)

1 1 1

2) 7615₈

+ 346₈

10163₈

5 +6 = 11 = 1*8 + 3 («1» переносится в старший разряд)

4 +1 + 1 = 6

6 + 3 = 9 = 1*8 + 1 («1» переносится в старший разряд)

7 + 0 + 1 = 8 = 1*8 + 0 («1» переносится в старший разряд)

1 1 1

3) 9FA₁₆

+ E836₁₆

F230₁₆

10 +6 = 16 = 1*16 + 0 («1» переносится в старший разряд)

15 +3 + 1 = 19 = 1*16 + 3 («1» переносится в старший разряд)

9 + 8 + 1 = 18 = 1*16 + 2 («1» переносится в старший разряд)

0 + 14 + 1 = 15 = F

При вычитании чисел в р цифры вычитаются поразрядно. Если в рассматриваемом разряде необходимо от меньшего числа отнять большее, то занимается единица в следующем (старшем разряде). Занимаемая единица равна р единицам этого разряда (аналогично, когда занимаем единицу в десятичной системе счисления, то занимаемая единица равна 10.) Для двоичной системы счисления занимаемая единица = 2₁₀ = 10₂, для восьмеричной системы счисления занимаемая единица = 8₁₀ = 10₈, для шестнадцатеричной системы счисления занимаемая единица = 16₁₀ = 10₁₆.

Примеры: Точками в примерах с вычитанием отмечены разряды, из которых приходилось занимать.

   2

1) 11010₂

1101₂

1101₂

2 – 1 = 1 (так как 0 < 1 пришлось занять из соседнего разряда)

0 – 0 = 0

2 – 1 = 1 (так как 0 < 1 пришлось занять из соседнего разряда)

В этом разряде остался 0, вновь пришлось занимать из старшего разряда: 2 – 1 = 1

В этом разряде остался 0

  8

2) 7615₈

346₈

7247₈

8 + 5 – 6 = 7 (так как 5 < 6 пришлось занять из соседнего разряда)

8 + 0 – 4 = 4 (после того, как заняли, в этом разряде остался 0)

5 – 3 = 2

7 – 0 = 7

   16

3) E836₁₆

9FA ₁₆

DE3C₁₆

16 + 6 – 10 = 12 = C₁₆ (заняли из соседнего разряда)

16 + 2 – 15 = 3 (В этом разряде осталась 2, заняли из соседнего разряда)

16 + 7 – 9 = 14 = Е₁₆

В этом разряде осталась D₁₆

Иногда при вычитании необходимо занимать единицу через несколько разрядов, так как в соседнем или в нескольких соседних разрядах подряд стоят нули. В этом случае надо иметь в виду, что в этих разрядах на месте нулей после того, как заняли, будет располагаться «последняя цифра» той системы счисления, в которой записано уменьшаемое, т.е. цифра 1 для двоичной, цифра 7 для восьмеричной и цифра F для 16-ричной систем счисления.

Примеры:

 1 1 2  7 7 8  F F 16

1000₂ 1000₈ 1000₁₆

11₂ 11₈ AD₁₆

101₂ 767₈ F53₁₆

Замечание. При выполнении арифметических операций с числами, которые находятся в разных системах счисления, необходимо перевести числа в одну и ту же систему и только потом выполнять действие. Конечно, можно в качестве такой системой счисления выбрать десятичную систему, однако, в случае, когда в числах много цифр, такой перевод будет трудоемким. Например, при переводе числа 123456789ABCDEF₁₆ в десятичную систему придется вычислять 16 в степенях вплоть до четырнадцатой.

Умножение в позиционной системе счисления является достаточно сложным действием, поэтому более надежно умножение выполнять в 10-тичной системе с предварительным и завершающим переводом в исходную систему. Однако умножение на 2 можно представить в виде суммы. Например: 2*Т, где Т = 315₈

2 * 315₈ = 315₈

315₈

632₈

При умножении на 7₁₀, 8₁₀, 9₁₀ можно воспользоваться переводом в десятичную систему. Но так как десятичное число 8 равно 8-ричному числу 10 (8₁₀ = 10₈), тогда умножение можно заменить умножением на десять с последующим вычитанием или сложением.

Примеры:

1) 8₁₀ * 6271₈ = 10₈ * 6271₈ = 62710₈

2) 7₁₀ * 6271₈= (8₁₀ – 1₁₀) * 6271₈ = (10₈ – 1₈) * 6271₈ =

= 62710₈

6271₈

54417₈

3) 9₁₀ * 6271₈= (8₁₀ + 1₁₀) * 6271₈ = (10₈ + 1₈) * 6271₈ =

= 62710₈

6271₈

54417₈

Замечание. Если второй сомножитель представлен в двоичной или шестнадцатеричной системе, его предварительно необходимо перевести в восьмеричную систему счисления, например: 7₁₀ * А3С5₁₆.

Сначала переведите А3С5₁₆ в восьмеричную систему, используя метод тетрад и триад, а затем выполните умножение.

А3С5₁₆ = 1010 0011 1100 0101₂ = 001 010 001 111 000 101₂ = 121705₈.

7₁₀ * 121705₈ = (8₁₀ – 1₁₀) * 121705₈ = (10₈ – 1₈) * 121705₈ =

= 1217050₈

121705₈

1075143₈

При умножении на 15₁₀, 16₁₀, 17₁₀ можно воспользоваться тем фактом, десятичное число 16 равно 16-ричному числу 10 (16₁₀ = 10₁₆). В этом случае, как и в предыдущем, умножение можно заменить умножением на десять с последующим вычитанием или сложением.

Примеры:

1) 16₁₀ * A6D5₁₆ = 10₁₆ * A6D5₁₆ = A6D50₁₆

2) 15₁₀ * A6D5₁₆= (16₁₀ – 1₁₀) * A6D5₁₆ = (10₁₆ – 1₁₆) * A6D5₁₆=

= A6D50₁₆

A6D5₁₆

9C67B₁₆

3) 17₁₀ * A6D5₁₆= (16₁₀ + 1₁₀) * A6D5₁₆ = (10₁₆ + 1₁₆) * A6D5₁₆=

= A6D50₁₆

= A6D50₁₆

A6D5₁₆

B1425₁₆

Замечание. Если второй сомножитель представлен в двоичной или восьмеричной системе, его предварительно необходимо перевести в шестнадцатеричную систему счисления, например: 17₁₀ * 7154₈.

Сначала переведите 7154₈ в шестнадцатеричную систему, используя метод тетрад и триад, а затем выполните умножение.

7154₈ = 111 001 101 100₂ = 1110 0110 1100₂ = E6C₁₆.

17₁₀ * E6C₁₆ = (16₁₀ + 1₁₀) * E6C₁₆ = (10₁₆ + 1₁₆) * E6C₁₆=

= E6C0₁₆

E6C₁₆

F52C₁₆

Примеры выполнения задания 1.

Пример 1. Найти шестнадцатеричное решение уравнения

X = M + 7*L - T + P ,

где 7 - десятичное число,

M - десятичное число M=3256 ,

P - шестнадцатеричное число P=A01 ,

L - шестнадцатеричное число L= FAC ,

T - восьмеричное число T= 7665.

Решение:

Преобразуем к виду

X = (M + 7 *L + P) – T