Енергетичний зміст рівняння Бернулі.

Всі чотири доданки рівняння (1) виявляються питомими енергіями (віднесеними до ваги рідини) потоку.

При усталеному русі рідини сума 4-х питомих енергій (енергії положення, енергії гідродинамічного тиску, кінематичної енергії і енергії втрат напору) залишається незмінною повздовж потоку.

П овна енергія (у вигляді напору) у потоці вимірюється трубкою Пітто (динамічною трубкою), яка має форму перевернутої букви Г, спрямованої назустріч потоку. П’єзометричний напір вимірюється п’єзометричною трубкою з гладким кінцем.

Рис. 18. Розташування тисків до визначення гідравлічного і п'єзометричного ухилів.

З’єднавши рівні рідини у п’єзометричних трубках, отримаємо лінію п’єзометричного напору або лінію питомої потенційної енергії . Падіння напору п’єзометричного напору на одиницю довжини l називається п’єзометричним ухилом I:

П’єзометричний ухил може бути як позитивним, так і негативним.

Падіння лінії повного напору на одиницю довжини називається гідравлічним ухилом і:

Гідравлічний ухил, згідно закону збереження енергії, може бути виключно позитивним у напрямку руху потоку.

Рівняння Бернуллі для елементарної струминки реальної довжини для будь-якої точки, де рідина рухається з місцевою швидкістю :

Рівняння Бернуллі для ідеальної рідини буде відрізнятися від виразів (1) і (2) відсутністю доданку , відповідному питомої енергії втрат напору.

Рівняння Бернуллі справедливо для ідеального і реального газу, якщо для нестислого газу подається у формі тисків. Для струминки ідеального газу:

Виміри тиску газу проводять за допомогою виключно манометів, швидкісним напором зневажають. Для стислого газу рівняння Бернуллі вивчається у курсі аеродинаміки.

Водомір Вентурі.

Водомір Вентурі використовують для вимірення витрат рідини по показанням п’єзометричних трубок. Різниця їх п’єзометричних напорів залежить від величини витрати.

Складемо рівняння Бернуллі для перерізів 1-1 і 2-2 без урахування втрат напору.

Рис. 19. До принципу дії водоміра Вентурі.

і хай z₁=z₂, =1

Виразимо швидкості крізь відношення площ перерізів з урахуванням закону нерозривності потоку:

Q₁=Q₂

V_{1 1}=V_{2 2}

Тут k– тарировочний коефіціент, необхідний для побудування тарировочної кривої для кожного конкретного водоміру. По цієї кривої потім визначається витрата Q по виміреній величині переспаду у п’єзометричних трубках.

На базі рівняння Бернуллі роботають такі пристрої, як водострумний насос (ежектор) та інжекційний газовий пальник.

Лекція 6.

Гідравлічні опори. Два режими руху рідини. Визначення втрати напору по довжині.

Для ідеальної рідини всі задачи вирішуються системою двох рівнянь.

Для реальної рідини, яка має властивість в’язклсті, у систему додається 3-є рівняння, і система обретає вид:

За допомогою цієї системи вирішуються всі гідродинамічні інженерні задачи. Аналогічно – аеродинамічні.

Існують дві групи втрат напору:

Перша – на тертя або по довжині.

Друга – на місцеві опори – при протіканні рідини крізь будь-якого рода перешкоди (коліна, відводи, трійники, заслінки тощо).

Обидва види втрат напору можуть бути знайдені досліддим шляхом – це підходить для існуючих водоводів та інших систем комунікацій. Наприклад, на існуючому водоводі втрати напору на діляянці 1-2.

, де d=const

V=const, =const

Рис. 20. Визначення втрат напору по довжині дослідним методом.

Складемо рівняння Бернуллі для потоку реальної рідини для перерізів 1-1 і 2-2.

Таким же чином п’єзометри установлюються до та після місцевого опору та визначають втрати напору h_m на місцевому опорі.

при =1

Рис.21. Визначення втрат на місцевих опорах дослідним методом.

Витрати напору рідини при її русі складаються з суми втрат на тертя і на місцеві опори:

Шляхом розрахунку, для проектування , втрати напору на гідравлічне тертя визначаються, в загальному випадку по формулі Дарсі-Вейсбаха:

(1)

Тут - коефіціент гідравлічного тертя, безрозмірна величина (коефіціен Дарсі).

l - довжина трубопроводу, м.

d - діаметр трубопроводу, м.

- середня швидкість потоку, м/с, на ділянці.

Місцеві втрати напору визначаються по формулі Вейсбаха:

Тут - коефіціент місцевого опору, безрозмірна величина, яка залежить від виду місцевого опору.

- середня швидкість на ділянці за місцевим опором, м/с.

Коефіціенти і залежать від багатьох факторів, головним з яких є режим руху рідини та жорсткість стінок водоводу.

Два режими руху рідини.

В 1983 році английский вчений Рельнольдс довів наявність 2-х режимів руху частинок рідини. Крізь скляну трубку пропускали воду з середньою швидкістю V.

1 – бак постійного напору.

2 – бачок з забарвленою рідиною.

3 – скляна трубка.

4 – перливна трубка.

5 – регулюучи вентилі.

6 – тонка трубочка із загостреним струмноспрямуючим кінцем.

Рис. 22. Дослід Рейнольдса по визначенню двух режимів руху рідини.

При малих швидкостях V руху води лінія забарвленої рідини не перемішується з рештою води в трубці 3. При деякії критичнії швидкості V_кр струминка забарвленої рідини розмивалася в контурі та перемішувалася з рештою води. Тобто, можна сказати, що рух частинок рідини в першому випадку мав паралельнострумний характер, а в другому випадку – хаотичний.

Перший режим руху рідини називається ламінарним (паралельнострумним), а другий – турбулентним (безладним) (досліди довели, що вид режиму залежить від безрозмірного параметру, або критерія Рейнольдса Re, або числа Рейнольдса.

Тут V - середня швидкість потоку в трубі, м/с;

d - діаметр труби, м;

- кінематична в’язкість, м²/с.

Число Рейнольдса, при котрім ламінарний рух переходить до турбулентного, називається критичним

При тому відповідна швидкість називається критичною:

Практично, це число знаходиться в межах 1000 4000.

Для відкритих русіл (безнапорний рух)

Тут R - гідравлічний радіус, м. Практично це число дорівнює 300-500.

Росподіл швидкостей та втрати напору при ламінарносму режимі руху рідини в трубках.

При ламінарному русі потоку шари рідини рухаються паралельно один до одного. Епюра швидкостей по перерізу трубки має характер дуже витянутої параболи з вершиною на вісі труби. Значення максимальної швидкості на вісі труби _мах:

- питома вага рідини;

d - діаметр труби;

- динамічна в’язкість;

i - гідравлічний ухил.

Росподіл місцевих швидкостей по перерізу підкоряється закону параболи:

i - гідравлічний ухил;

r - радіус труби;

y - відстань до вісі труби від обраної точки перерізу по вертикалі (всі значення параметрів подають у системі СІ).

Середня швидкість при ламінарному русі дорівнює половині максимальної:

Коефіціент Коріоліса  при ламінарному русі дорівнює 2.

Втрати напору при ламінарному русі визначається по формулі Пуазейля і пропорційні швидкості у першому ступені.

Як бачимо, жорскість стінок не є зумовним фактором при знаходженні коефіціента гідравлічного тертя і втрат напору по довжині.

Розподіл швидкостей і визначення втрат напору при турбулентному режимі руху

рідини в трубах.

При турбулентному режимі швидкість руху в кожній точці змінюється по величині та напрямку, тобто відбувається пульсація швидкості навколо деякого середнього значення, що називаєтья середньою місцевою швидкістю.

Осереднена швидкість умовно видається сталою в точці, що розглядається, та спрямованою паралельно вісі потоку. Цей рух по осередненим швидкостям можемо ураховувати паралельнострумним та застосовувати до нього рівняння Бернуллі. Осереднена швидкість потоку, далі буде визнаватися місцевою швидкістю в даної точці.

Всі рішення розподілу швидкостей потоку по перерізу мають напівемпіричний характер (напівдослідний). Виявлено, що розподіл швидкостей по перерізу також, як і при ламінарному русі, має характер параболи, але ця парабола значно меньш витягнута повздовж вісі. Закон розподілу швидкостей ураховує дотичні напруження повздовж стінок

- динамічна швидкість або швидкість дотичного напруження, м/с.

х - універсальна постійна Прадтнля, яка дорівнює приблизно 0,4.

- коефіціент Дарсі.

Співвідношення середньої і максимальної швидкостей дорівнює 0,7 0,9.

Коефіціент Коріоліса =1,031,2. Це свідчить про більш рівномірний розподіл швидкостей по перерізу труби в результаті їх пульсації.

(Ламінарний рух)

(Турбулентний рух)

Рис. 23. Розподіл швидкостей у трубі в двох режимах руху рідини.

Німецький вчений Прандтль створив напівемпіричну теорію турбулентності. Згідно з нею, в трубі потік розподіляється на турбулентне ядро і тонкий ламінарний шар по периметру стінки з виступами жорсткості К_е (або Δ_е) .

Дослідження вчених Нікурадзе і Мурина дозволили отримати напівемпіричні формули і графіки для визначення коефіціента  і обчислення втрат напору по формулі (1) при турбулентному режимі руху рідини у трубах. Це є основний розрахунковий режим при проектуванні.

Графік Муріна.

Графік – це залежність , де:

- відносна шорсткість труби (для різноманітних труб d_i зроблено узагальнення).

К_е – еквівалентна шорсткість, тобто утворена штучно при котрій досягається такий гідравлічний опір по довжині, як з природною шорсткістю того ж діаметру. Вона дорівнює по висоті діаметру фракцій тиску, який утворює її штучно.

Рис.24. До визначення еквівалентної шорсткості русла (наприклад, труби) при d=h трикутного виступа реальної шорсткості і штучно утвореного виступу шорсткості, створеного круглою частикою піску.

Рис.25. Графік Муріна.

Спостерігаємо наявність трьох областей:

1 - Гідравлічно гладких труб (малі числа Рейнольдса R_e при малих швидкостях руху). В цієї області співвідношення поміж Rе і d/Kе.

Більша товща ламінарність шару перевищює висоту виступів шорсткості. Він як-би, обіймає їх, тому шорсткість труби не впливає в значній мірі на коефіціент гідравлічного тертя:

У цієї області =f(Rе), тому втрати напору пропорційні швидкості в ступені 1,75, тому вони залежать від швидкості нелінійно.

2 – певно шорстких труб або квадартична зона опору.

В цієї області товща ламінарного шару мала, в поривнянні з висотою виступів шорсткості Ке, тому шорсткість труби не виказуює визначений вплив на величину 

Це відбувається, коли Rе500d/ Ке_.

Виступи шорсткості тут завище за ламінарний шар і стінки не блокується їм. В цієї області втрати напору виявляються пропорційними до квадрату швидкості:

Тому ця зона називається квадратичною зоною втрат напору.

Рис. 26. Турбулентні зони гідравлічного опору.

3 – перехідна. В цієї області гідравлічного опору коефіціент  має вплив на Rе,

також d/ Ке, оскільки товща ламінарного шару співвимірна з висотою виступів жорсткості.

 визначається по формулі Альтшульса:

Це відбувається, якщо .

В цієї області втрати напору залежать від швидкості у ступені від 1,75 до 2-х.

Зокрема наведених залежностей, у довідниках з гідравлики наведені формули Кольбрука, Прандтля, Блазіуса, Шевелева та інших авторів задля будь-яких випадків співвідношень Rе і d/ Ке_.

Вчений Ф.А. Шевелєв розробив таблиці для гідравлічного розрахунку сталевих, чавунних, пластмасових, скляних, бетонних та залізобетонних труб промислового зразку. Ці таблиці використовують у теперішнім часі при поектуванні промислових трубопроводів.

Ті ж автори розробили дослідні формули для аеродинаміки. Коефіціент  для газів визначається для розрахунків проомислових газопроводів і повітропроводів (тобто з урахуванням стиснення газу та без нього).

Лекція 7.

Місцеві гідравлічні опори.

Місцеві опори – це опори перешкод, що обтікаються рідиною. При наявності таких перешкод відбувається відрив потоку і утворення віхрових зон. На деформацію ліній току в цих зонах втрачається частка енергії потоку. Втрати напору на місцеві опори підрозділяються:

1. Втрати, пов’язані зі змінами перерізу трубопроводу (раптове або повільне звуження чи розширення);

2. Втрати, пов’язані зі зміною напрямку руху потоку (кутники, відводи);

3. Втрати, пов’язані з протіканням рідини крізь арматуру (вентилі, заслінки, диафрагми, зворотні клапани тощо);

4. Втрати, пов’язані з розділом чи злиттям потоку (трійники, хрестовини);

5. Втрати на зварних стиках трубопроводів.

Всі місцеві опори можуть бути визначені дослідним шляхом як різність показань п’єзометрів або манометрів (дивись лекцію 6).

Шляхом розрахунку всі місцеві опори визначаються по формулі Вейсбаха:

Взагалі, задача полягає в тому, щоб визначити коефіціент місцевого опору . Більшість коефіціентів визначаються по емпірічним формулам. Невелика група коефіціентів визначається теоретично на підставі теореми Борда-Карно.

Втрати напору при раптовому розширенні трубопроводу (теорема Борда-Карно).

В трати напору при раптовому або різькому розширенні потоку дорівнюють швидкісному напору втраченої швидкості.

Рис. 27. Втрати напору на „класичному” гідравлічному опорі „

раптовому розширенні трубопроводу” – до теореми Борда-Карно.

Застосуємо теорему імпульсів класичної механіки до ділянки рідини поміж перерізами 1-1 і 2-2.

Проекція на повільно визначену вісь (вісь трубопроводу) прирощення кількості руху дорівнює сумі імпульсів зовнішних сил, що діють на ділянку, що розглядається, за певний час (нехай час Т=1с):

Із зовніших сил в рівняння включаємо тільки силу гідродинамічного тиску Р, тому що силу тертя на малої ділянці не враховуємо.

- сума сил в напрямку руху потоку – сума сил тиску.

Поділимо це останнє рівняння на та приймемо =1

*

Складемо рівняння Бернулі для перерізів 1-1 і 2-2 та підставимо з рівняння  його частину

Втрати напору в діфузорах (трубках, що повільно розширюються). Діфузор характеризується кутом розкриття чи конусністю.

Рис. 28. Втрати напору на повільному розширенні потоку

(діфузорі)

Тут h_диф - втрати напору у діфузорі

- коефіціент гідравлічного опору

h_р-р - втрати напору на раптовому розширенні

k - коефіціент пом’якшення.

Втрати напору в діфузорі будуть меньші, ніж при раптовому розширенні потоку, оскільки віхорові зони повільно згладжуються.

Втрати напору в діфузорі визначаються як для раптового розширення, але з помноженням на коефіціент зм’якшення к1, який залежить від куту конусності .

Значення кофіціентів наведені в довіднику Кисильова.

- оптимальне зниження .

Рис. 29. Область оптимального значення коефіциєнта зм’якшення К

Втрати напору при раптовому звуженні потоку.

Рис. 30. Визначення втрат напору на „раптовому звуженні” потоку.

Частинки рідини, які входять в вузький переріз намагаются зберегти свою траекторію за інерцією та формують так званий стиснений переріз _c.

Втрати напору, взагалі, виникають при розширенні перерізу від _c. до ₂.

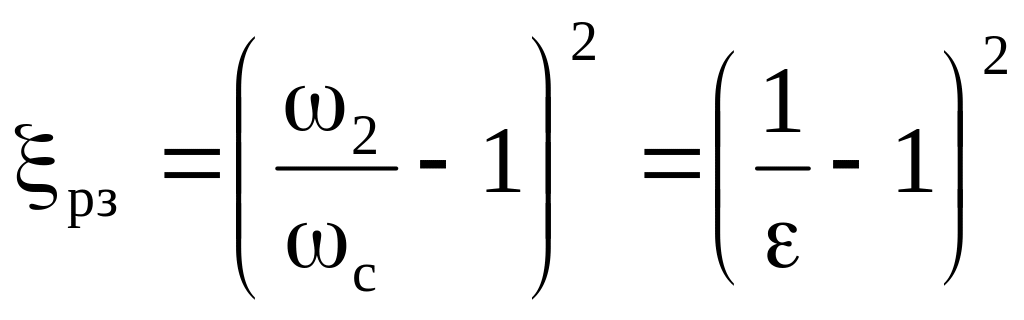
Тут - ступінь стиснення струмини, чи коефіціент стиснення.

_c. - стиснений переріз вимірити дуже складно, тому в розрахунках використовують емпірічні значення по таблицях, наприклад, в довіднику Кисильова [4].

При ₁>> ₂ =0.611 (стечіння з резервуару) =0.42

Втрати напору в повільно звуживаючихся трубах (конфузорах).

Рис. 31.Втрати напору на повільному звуженні потоку (конфузорі)

Втрати напору визначаються також, як для раптового звуження, але з помноженням на кофіціент пом’якшення, який є меньш за одиницю. У відповідності до куту конусності 1 в довідниках подається графічна або таблична залежність.

Рис. 32. Область оптимального значення коефіциєнта зм’якшення К₁

Значення для конфузорів наведені в довіднику Кисильова [4] в залежності від співвідношення більшого та меньшого перерізів.

Втрати напору у відводах, колінах, кутниках.

Коліни утворюють тим більші гідравлічні опори, чим більш різький їх поворот, тобто чим меньший їх радіус заоколення R. Коліно вдається гострим, якщо r=R. Для такого коліна =1. Взагалі для більш повільних колін та відводів в довіднику Кисильова [4] наведені значення .

Рис. 33. Втрати напору у коліна, відводах, трикутниках.

, де в залежності від співвідношення R/d.

Втрати напору в діафрагмах.

Діафрагма – штучне утворене раптове звуження потоку в трубопроводах. Вона існує для гасіння напору, або для виміру витрати (вимірювальна діафрагма). В останьому випадку ураховується зв’язок втрат напору з величиною швидкості та витрати в трубопроводі.

Рис. 34. Втрати напору в діафрагмах.

, де

Значення та подані в таблицях довідника Кисильова [4].

Втрати напору в трійниках.

Існують дві групи трійників – нагнетаючі та всмоктуючі, або припливні (1) та втяжні (2).

Рис. 35. Схеми до визначення коефіциентів місцевих опорів для трикутников або

хрестовин.

В трійниках відрізняють магістраль та відгалуження.

Поворіт потоку може відбуватися на кут 90.

Втрати напору залежать від схеми роботи трійника в потоці, від куту між магістральними напрямком та відгалудженням , від співвідношення їх діаметрів та h_m залежать, до якої швидкості їх віднести: до магістралі чи до відгалудження, до чи після відгалудження. Всі можливі схеми наведені в довіднику Кисильова [4].

Втрати напору в заслінках і вентилях.

Втрати напору в заслінках і вентилях виникають в результаті зменьшення перерізу трубопроводу. Взагалі, як для раптового звуження потоку.

Рис. 36. Втрати напору в заслінках та вентилях.

Значення подані в довіднику Кисильова, в залежності від ступення відкриття заслінки або вентилю. Але повністю відкрита арматура утворює опір своїм клапаном. Для повністю відкритої заслінки рекомендується брати =0.1, а для повністю відкритого вентеля =5 [4].

Втрати напору на зварних стиках.

Втрати напору на зварних стиках визначаються по експереминтальним залежностям. Досліди показали, що вплив стиків можна розглядати як збільшення коефіціента гідравлічного тертя .

Рис. 37. Вплив стиків труб на збільшення гідравлічного тертя.

- індивідуальний опір стику (по довіднику Кисильова від засобу зварювання).

 - коефіціент Дарсі без стиків.

’- те ж зі стиками.

Залежність коефіціентів місцевих опорів від числа Рейнольдса.

Рис. 38. Визначення коефіциентів гідравлічних опорів в не квадратичній області

гідравлічного опору.

Для великих чисел Рейнольдса, відповідних квадратичнії зоні гідравлічного опору, залежність =f(Rе) зникає. При малих числах Rе­ – залежить значно. Довідні значення обчислені для квадратичної області опору. Для переходу в другі області є формула:

, де

А – довідна величина, яка дається в залежності від значення Rе­_.

Взаємний вплив місцевих опорів.

При гідравлічному розрахунку втрати напору можна складати по всім розташованим там місцевим опорам тоді, коли вони знаходяться на відстані одного від одного, більш ніж відстань впливу.

Відстань впливу – це відстань, на якій епюра швидкостей, деформована попереднім місцевим опором, відновлює форму. Відстань впливу визначається з співвідношення:

- калібр труби. Для інженерних розрахунків припускається =2030.

В іншому випадку опори сумуються також, але додається коефіціент запасу, який ураховує зниження точності розрахунків.

Лекція 8.

Витікання рідини з отворів та насадків.