Учреждение образования
«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»
кафедра математики и физики
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ОСНОВНЫЕ СПОСОБЫ ИНТЕГРИРОВАНИЯ
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
для студентов заочной формы обучения уровня ССО
всех специальностей
Минск 2006
Составитель Т.К. Гресюк
Рецензент Е.Н. Ермаш
Издание утверждено на заседании кафедры М и Ф
18 мая 2006 года, протокол №10
Зав. кафедрой Л.Л. Гладков
Начиная изучение темы «Неопределенный интеграл» необходимо хорошо изучить темы:
«Понятие о производной функции»;
«Формулы дифференцирования»;
«Дифференциал функции».
Повторим предыдущий материал, с которым тесно связана новая тема по следующим вопросам:
1) Имея функцию, можно ли найти ее производную?
Ответ: можно, по известным формулам дифференцирования.
2) Можно ли по данному закону движения тела найти его скорость?
Ответ: можно, скорость – это есть производная пути по времени (механический смысл производной).
3) По данному уравнению кривой можно ли найти угловой коэффициент касательной, проведенный к этой кривой?
Ответ: можно, применяя знание геометрического смысла производной.
4) Можно ли по данной функции найти дифференциал?
Ответ:
можно
.
5) С помощью какого действия мы решали все эти четыре задачи?
Ответ: дифференцированием.
6) Что называется дифференцированием?
Ответ: математическое действие, с помощью которого по данной функции находим ее производную, или ее дифференциал, или по данному закону движения тела находим скорость его, или по данному уравнению кривой определяем угловой коэффициент касательной, проведенной к этой кривой, и т.п. называется дифференцированием.
7) Какое условие в этом действии является исходным, и что получаем, применяя данное действие?
Ответ: исходным условием является функция, а получаем или производную, или дифференциал, или скорость, или угловой коэффициент.
Однако часто приходится решать и обратную задачу: по известной скорости движения тела установить закон его движения, по данному угловому коэффициенту касательной к кривой находить уравнение этой кривой и т.п., иначе говоря, по данной производной отыскивать функцию, от которой произошла эта производная.
Заметим, что находить функцию можно не только по данной ее производной, но и по ее дифференциалу, так как производная функции и ее дифференциал связаны простым соотношением
;
.
Практически же отыскивать функцию удобнее по ее дифференциалу, поэтому в дальнейшем изложении мы и будем пользоваться дифференциалом для решения обратной задачи.
Возьмем несколько функций
;
;
;
,
где
.
Дифференциал, каждой из них один и тот же
.
Решим обратную задачу: по данному дифференциалу найти саму функцию.
Этому дифференциалу соответствует множество функций, отличающихся свободным членом.
Чтобы решение обратной задачи записать письменно, необходимо ввести кое-какие новые понятия.
Пусть функция
, (1)
имеет производную
,
тогда ее дифференциал
. (2)
Функция
по отношению к ее дифференциалу
называется первообразной.
Определение 1. Первообразной
функцией для
выражения
называется функция
,
дифференциал которой равен
.
Однако дифференциалу функции соответствует не единственная первообразная (как мы уже видели), а их множество, причем они отличаются друг от друга постоянным слагаемым.
Так нашему дифференциалу
соответствует множество
первообразных функций вида
,
где
– любая постоянная.
Выражение
называется неопределенным
интегралом для
дифференциала
и обозначается
,
то есть
.
Определение 2. Совокупность
всех первообразных функций
для дифференциала
называется неопределенным
интегралом и
обозначается
.
Таким образом, можно записать
,
где 
– знак интеграла;
– подынтегральное выражение;
– произвольная постоянная интегрирования;
– совокупность первообразных функций;
– подынтегральная функция.
Процесс нахождения первообразной функции называется интегрированием, а раздел математики, занимающийся вопросами, связанными с интегрированием – интегральным исчислением.
Из сказанного видно, что интегрирование есть действие обратное дифференцированию.
Определение 3. Математическое действие, с помощью которого по данной производной, или дифференциалу находится сама функция, или по известной скорости движения тела устанавливаем закон его движения, или по данному угловому коэффициенту касательной к кривой находим уравнение этой кривой и т.п. называется интегрированием ( – знак интегрирования).
Теперь вы познакомились с новым математическим действием, которому название интегрирование.
С геометрической
точки зрения неопределенный интеграл
представляет собой семейство интегральных
кривых, каждая из которых получается
из любой кривой параллельным переносом
вдоль оси
(рис. 1)
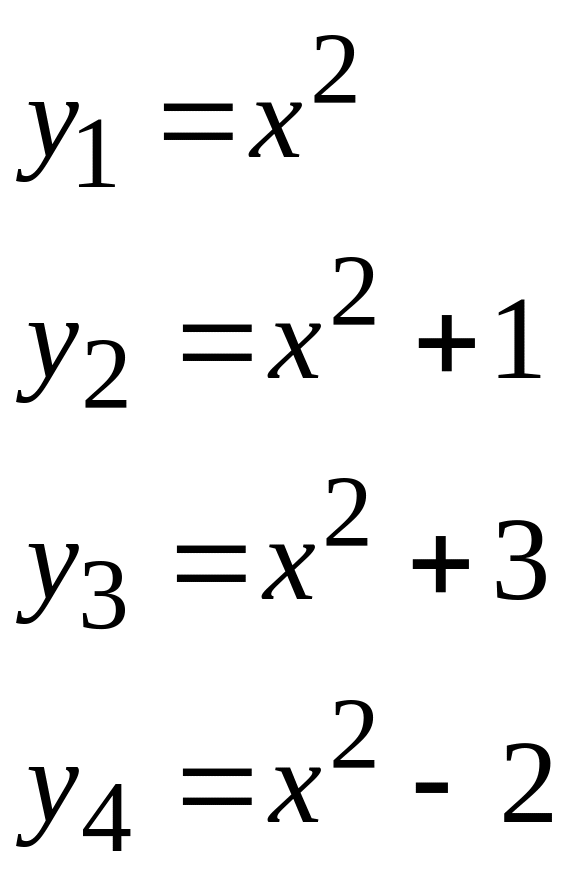
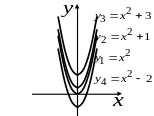
Рис. 1
График какой-либо первообразной функции называется интегральной кривой.
Если функция непрерывна на некотором промежутке, то на этом промежутке она и интегрируема, то есть существует .
Итак, вы знаете уже десять математических действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, логарифмирование, потенцирование, дифференцирование и интегрирование.
Каждое действие применяется при решении определенной задачи.
В каждом действии свои исходные данные и получается свой конечный результат.
Перед тем, как приступать к выполнению того или иного действия необходимо знать определенные законы, свойства, которым подчиняется это действие.
Вот сейчас мы рассмотрим основные свойства неопределенного интеграла.
Пусть функция
является первообразной для функции
на некотором промежутке
,
то есть
,
.
По определению .
Первое свойство. Производная неопределенного интеграла равна подынтегральной функции, то есть
.
Второе свойство. Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть
Это свойство следует из определения неопределенного интеграла
,
если
,
то есть
.
Третье свойство. Неопределенный интеграл от дифференциала некоторой функции равен этой функции, сложенной с произвольной постоянной
.
Пусть
.
Если возьмем интеграл от обеих частей этого равенства, то получим
.
Но по определению
,
следовательно
.
Примем без доказательства еще следующие свойства неопределенного интеграла.
Четвертое свойство. Постоянный множитель можно выносить за знак интеграла, то есть
,
где 
- постоянный множитель.
Пятое свойство. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждой из них, то есть
.
Для нахождения неопределенного интеграла еще необходимо знать основные формулы интегрирования.
1
(по второму свойству)
2
интеграл степени.
Докажем верность этого равенства.
Рассмотрим функцию
и найдем ее дифференциал
.
Взяв интеграл от обеих частей этого равенства, получим
.
Применяя второе свойство интеграла к левой части последнего равенства и третье свойство к правой части, найдем
,
отсюда, при
имеем
.
Обозначив постоянное
слагаемое
буквой
,
будем иметь окончательно
.
Выведенная формула
справедлива для любого значения
,
кроме
.
В последнем случае формула теряет смысл.
3
Докажем верность этого равенства.
Зададимся вопросом,
какая функция имеет своим дифференциалом
выражение
.
Такой является функция
,
так как
,
следовательно,
.
4
(легко получается, если применить формулы
дифференцирования).
5
Докажем это равенство.
По определению неопределенного интеграла имеем
,
,
.
Следовательно, записанное равенство (5) верно.
Далее запишем формулы, легко получаемые из формул дифференцирования.
6
7
8
9
10
11
Зная определение неопределенного интеграла, свойства неопределенного интеграла и основные формулы интегрирования, можно решать примеры и задачи с применение действия интегрирования.
Определение постоянной интегрирования
По определению неопределенного интеграла
постоянное слагаемое имеет произвольное значение, а потому неопределенный интеграл представляет собой множество первообразных функций, отличающихся друг от друга постоянным слагаемым. Чтобы из совокупности первообразных функций найти одну, отвечающую задаче, нужно иметь дополнительное условие.
Пусть, например,
требуется найти уравнение кривой,
проходящей через точку
,
зная, что наклон касательной к кривой
в каждой ее точке равен
.
Согласно геометрическому смыслу производной, имеем
,
то есть
,
откуда
.
Взяв интеграл от обеих частей последнего равенства, получим
или
. (1)
Равенство (1) не может служить ответом на вопрос задачи, так как оно содержит неопределенное постоянное . Чтобы получить определенный ответ (то есть единственную первообразную для данного дифференциала), воспользуемся дополнительными данными задачи, а именно координатами точки, лежащей на кривой, уравнение которой имеется.
Положив, что в уравнении
(1)
и
,
будем иметь
,
откуда
.
Итак, искомое уравнение кривой (то есть искомая первообразная функция, удовлетворяющая данному дополнительному условию) будет иметь вид
.
Способы интегрирования
Первый способ – непосредственное интегрирование.
Под непосредственным интегрированием понимается такой способ интегрирования, при котором данный интеграл путем тождественных преобразований, подынтегральной функции и применения свойств 3-5 производится к одному или нескольким табличным интегралам.
Пример 1. Найти
.
Решение
Применяя четвертое и третье свойство интеграла, а затем формул (1) и (2), получим
.
Здесь является алгебраической суммой четырех произвольных постоянных слагаемых, входящих составной частью в каждый интеграл.
Правильность решения всегда можно проверить. Для этого найдем дифференциал от полученной в ответе функции
.
В результате получили подынтегральное выражение, следовательно, интеграл найден верно.
Так всегда правильность своего решения можно проверить.
Пример 2. Найти
.
Решение
Применяя четвертое свойство интеграла, введя отрицательные показатели, а затем формулу (2), получим
.
Пример 3. Найти
.
Решение
Данный интеграл не подходит ни под одну из табличных формул, поэтому подынтегральное выражение преобразуем следующим образом, введя дробные показатели
.
Применим формулу (2).
Формула
верна для любого
,
кроме
.
Пример 4. Найти
.
Решение
Представим подынтегральное выражение в виде суммы четырех дробей, разделив почленно на каждую дробь
.
Применяя свойство (4) интеграл и формулы (2) и (3), получим
.
Интегралы, приводимые к табличным после линейного преобразования дифференциала
Рассмотрим некоторые линейные преобразования дифференциала
;
;
.
Дифференциал аргумента на измениться, если к аргументу прибавить постоянное число, то есть
.
, 
;
, 
;
,
где
.
Постоянный множитель можно выносить за знак дифференциала и вносить под знак дифференциала.
;
.
При умножении аргумента, стоящего под знаком дифференциала, на постоянное число, дифференциал изменяется во столько же раз, что и постоянное число.
Чтобы величина
дифференциала аргумента не изменилась,
при умножении аргумента на
,
где
,
необходимо сам дифференциал умножить
на дробь, обратную
,
то есть на
.
Пример 5. Найти
.
Решение
.
При решении применяли линейное преобразование дифференциала (3) и формулу интегрирования (6).
Пример 6. Найти
.
Решение
.
При решении применяли линейное преобразование дифференциала (3) и формулы интегрирования (4), (5), (7).
Пример 7. Найти
.
Решение
Этот интеграл приводится к табличному (10)
.
Выполним некоторые преобразования
.
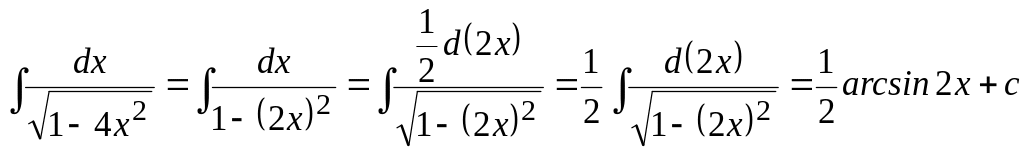Пример 8. Найти
Решение
Этот интеграл приводится к табличному
.
Выполним некоторые преобразования
.
Мы разобрали простейшие примеры, в которых функции могли быть выражены путем несложных преобразовании в виде, позволяющим применить для нахождения интеграла основные табличные формулы.
Для закрепления этого способа необходимо решить следующие примеры
1) Найти
Ответ:
2) Найти
Ответ:
3) Найти
Ответ:
4) Найти
Ответ:
5) Найти
Ответ:
6) Найти
Ответ:
Второй способ – способ подстановки.
Если заданный интеграл простейшими преобразованиями трудно привести (или совсем нельзя привести) к табличному, то для его отыскания применяются особые приемы. Одним из них является интегрирование способом подстановки. В основе метода подстановки лежит введение новой переменной, затем дифференцирование этой постановки, замена в искомом интеграле всего через новую переменную, а только потом использование основных формул интегрирования. После того, как нашли интеграл, опять возвращаемся к старой переменной.
Пример 9. Найти
.
Решение
Положим,
,
где 
- новая переменная.
Возьмем дифференциал от обеих частей равенства
.
Получим
,
,
.
Заменив в искомом
интеграле
и
их найденными значениями и применив
формулу (2)
будем иметь
.
Но ответ должен быть представлен как функция от переменной , поэтому, подставив вместо его значение из подстановки, получим
.
Пример 10. Найти
.
Решение
Введем подстановку
.
Продифференцируем равенство
,
получим
.
Подставим в подынтегральное выражение
.
Пример 11. Найти
.
Решение
Обозначим
.
Продифференцируем
,
,
.
Подставив в
подынтегральное выражение вместо
и
их значения, заменив корень степенью с
дробными показателями, а затем, введя
отрицательный показатель и применив
формулу интеграл степени, получим
.
Перейдя к прежней переменной , получим
.
Пример 12. Найти
.
Решение можно записать короче
,
,
.
.
Пример 13. Найти
.
Решение
Положим
,
продифференцируем
,
,
.
Заменив в искомом
интеграле
и
их найденными значениями и применив
свойство (3) и формулу (4), получим
.
Пример 14. Найти
Решение
Вводим подстановку
,
продифференцируем это равенство
,
.
Поставим вместо
и
в искомый интеграл
.
Замечание.
Если подынтегральное выражение содержит
и
одного и того же аргумента, причем одна
из функций входит в какой-либо степени,
то через новую переменную обозначают
первую степень той функции, которая
входит в степени.
При решении способом подстановки важно правильно выбрать подстановку, а для этого недостаточно простого знания формул, нужен еще опыт, который накапливается постоянно в процессе решения примеров.
Нужно устно выбранную подстановку продифференцировать и посмотреть остальное выражение в подынтегральном выражении можно ли заменить через новую переменную. Если можно, то выбранную подстановку верно выбрали. Если нет, то нужна другая подстановка. Запись решения следует производить так:
Пример 15.
.
Пример 16.
.
Пример 17.
.
Для закрепления интегрированием способом подстановки, необходимо решить следующие примеры:
Найти
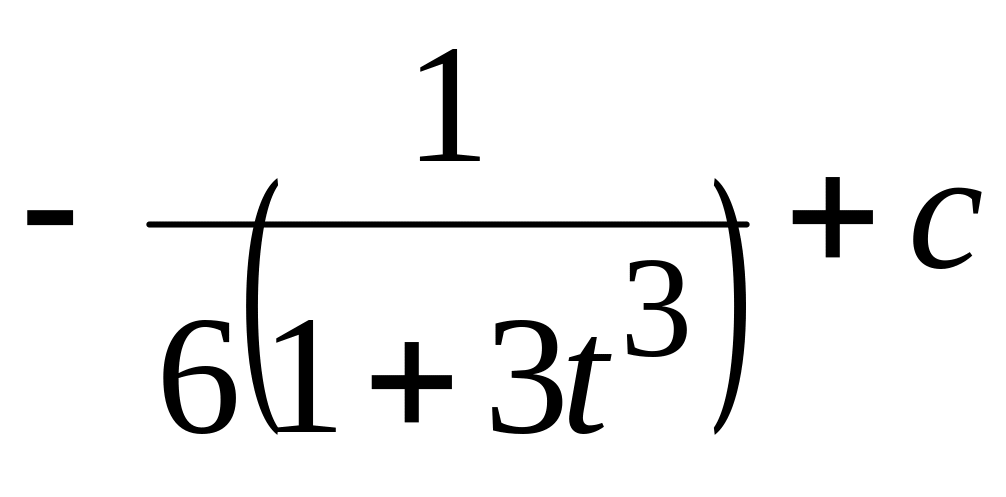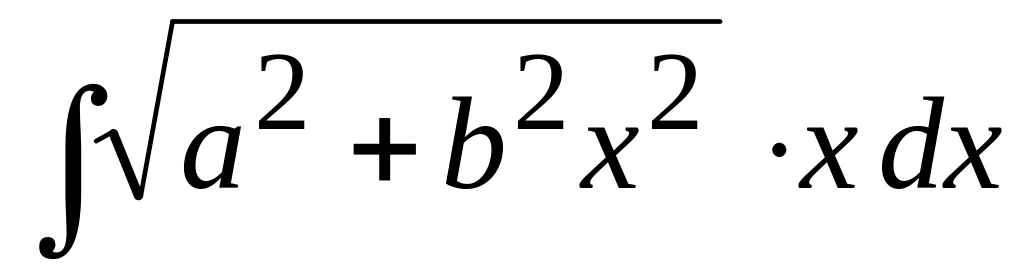Ответ:
;
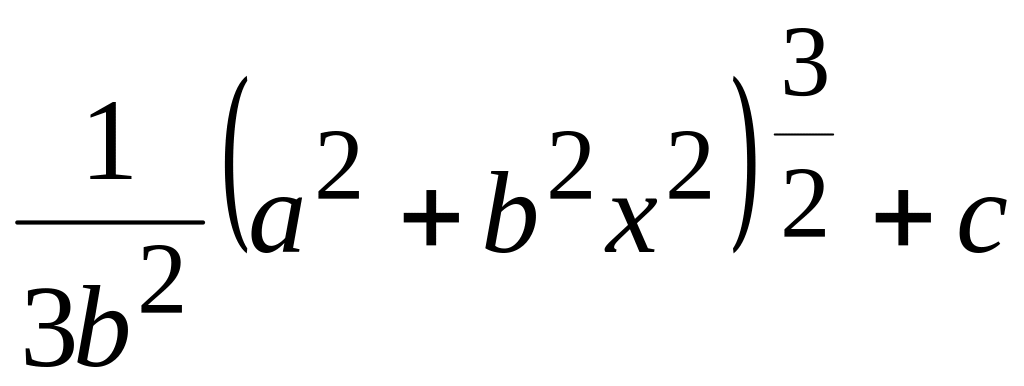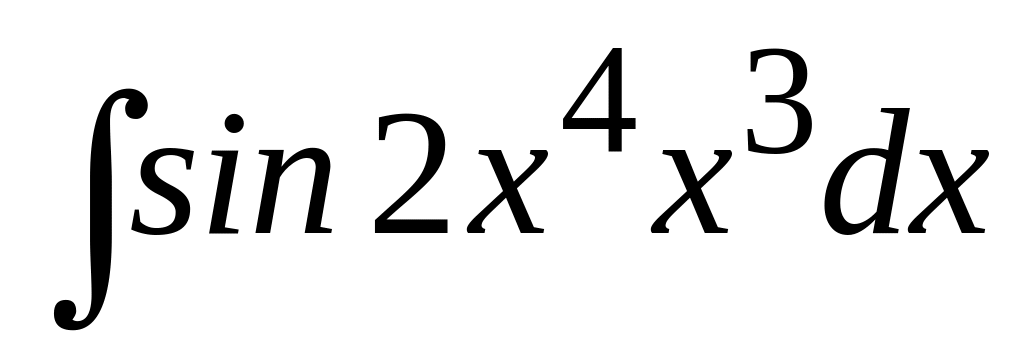Ответ:
;
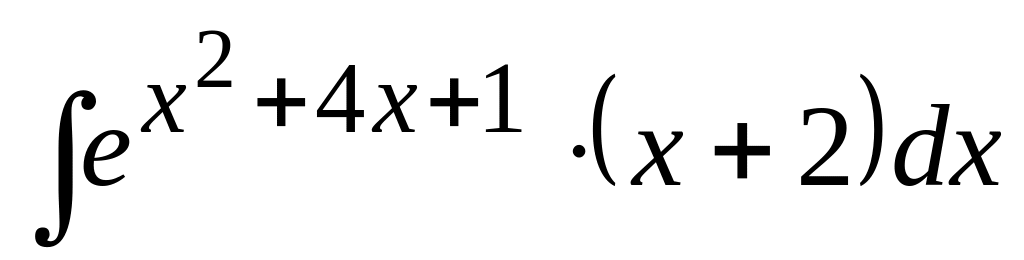Ответ:
;
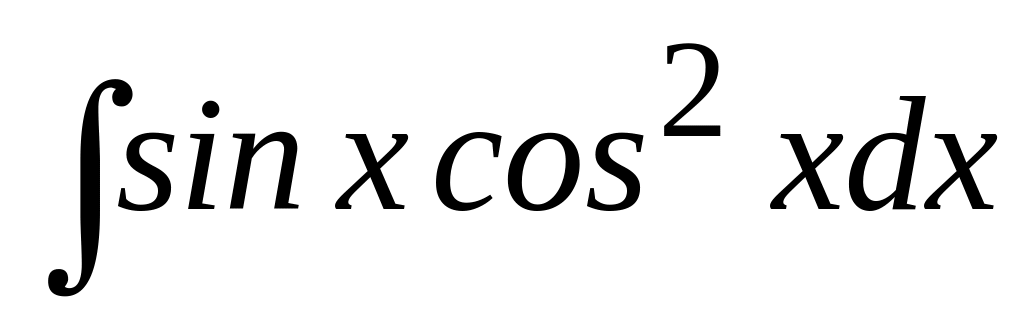Ответ:
;
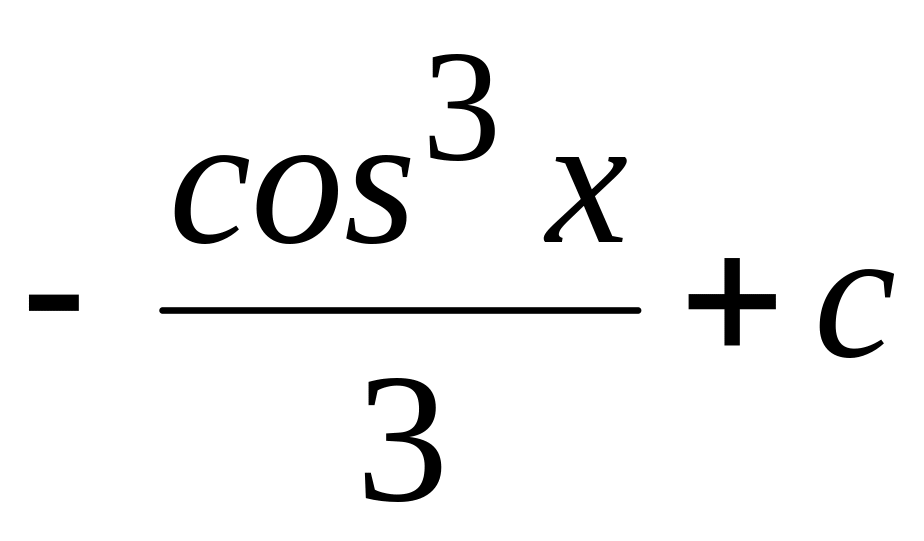Ответ:
;
Ответ:
.