2.5 Интегрирование иррациональных и тригонометрических выражений
Иррациональная функция – это функция, содержащая переменную под знаком радикала.
Если подынтегральное выражение содержит
иррациональность видов
и
,
где
,
то применяются подстановки соответственно
и
.
Пример 1.
.
Здесь
входит в подынтегральную функцию под
радикалами с показателями 2 и 3. Общее
наименьшее кратное показателей 6. Поэтому
делаем подстановку
,
тогда
,
.
Подставим в данный интеграл
.
Пример 2.
.
Если подынтегральное выражение содержит
иррациональность вида
,
то имеет место подстановка
.
Пример 3.
.
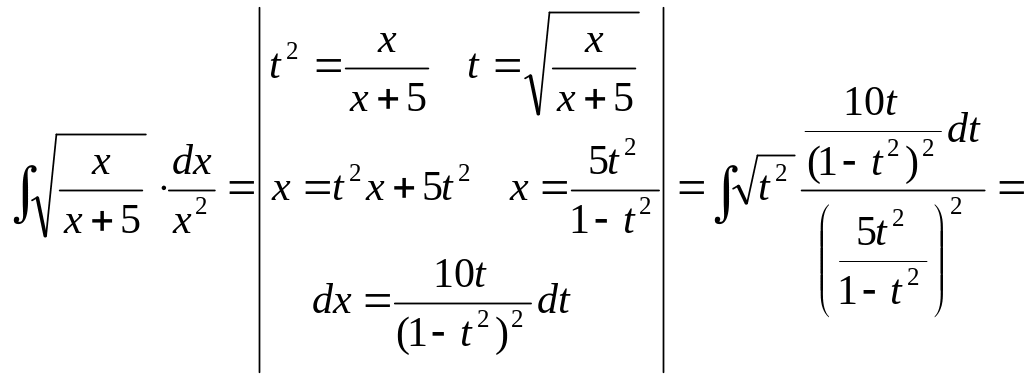
Если подынтегральное выражение содержит
иррациональности следующих видов:
,
,
,
то имеют место соответственно подстановки:
Пример 4.
.
Пример 5.
.
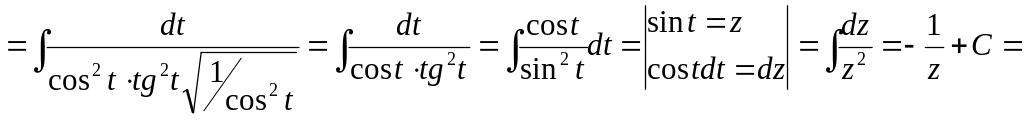
Пример 6.
=
.
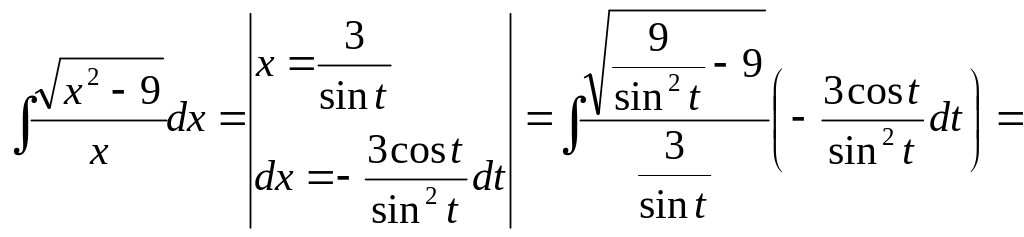
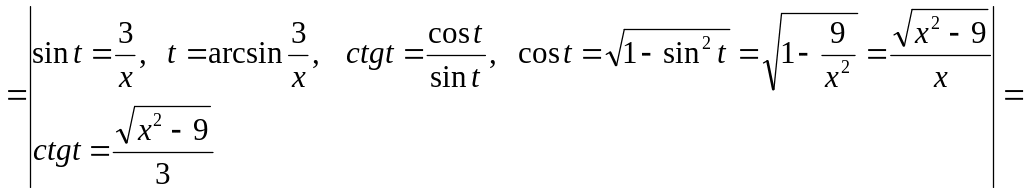
В зависимости от вида подынтегральной функции для упрощения тригонометрического выражения можно применять различные способы.
Для интегралов вида
:
а) если хотя бы одно из чисел
и
– нечетное (например,
),
то
.
Пример 1.
б) Если и – четные, положительные, то степени понижаются сведением к двойному углу по формулам
Пример 2.
в) Если
и
– четные и хотя бы одно из них отрицательно
(или если
и
– отрицательные числа одинаковой
четности), то используем замену
или
(тогда
)
и соотношения
;
.
Пример 3.
Пример 4.
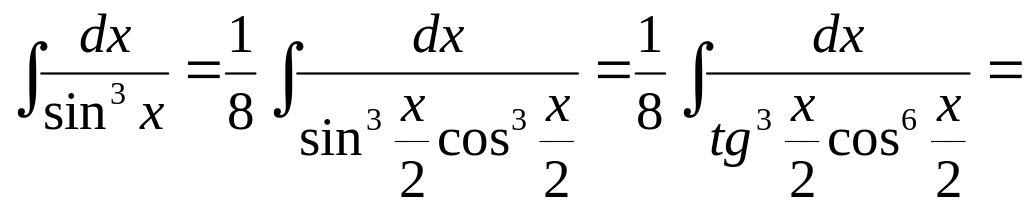
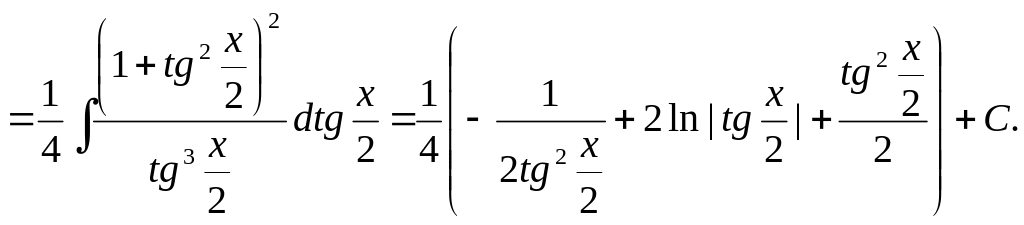
Интегралы вида
приводятся к табличным с помощью формул:
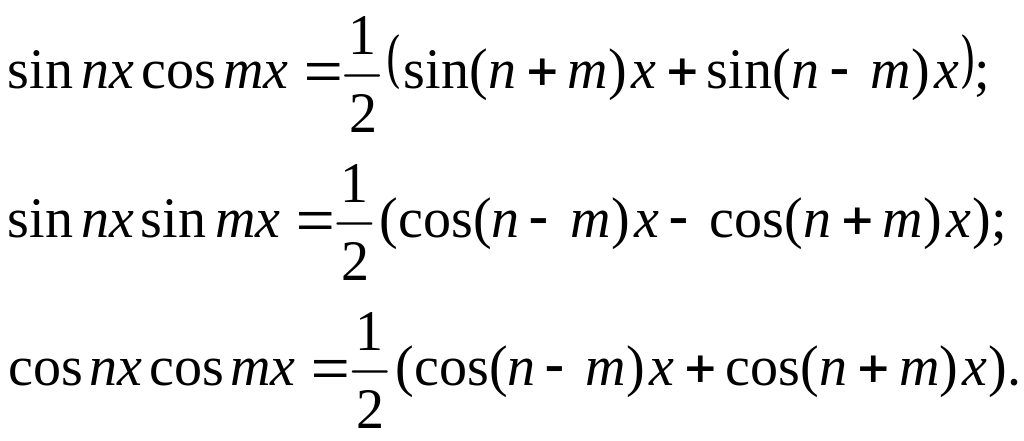
Пример 5.
Интегралы вида
,
где
– рациональная функция, приводятся к
интегралам от рациональных функций
новой переменной
в общем случае с помощью подстановки
,
откуда
.
Пример 6.
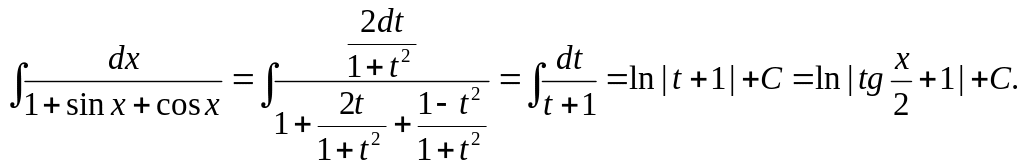
В случае четности
по
и
используем подстановку
,
откуда
.
Пример 7.
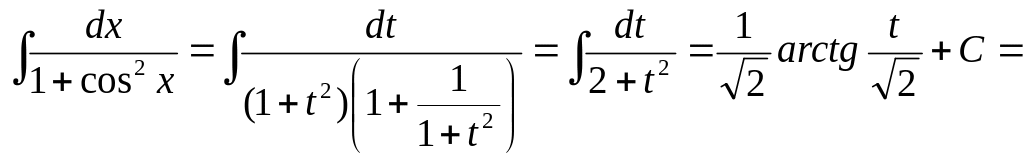
Пример 8.
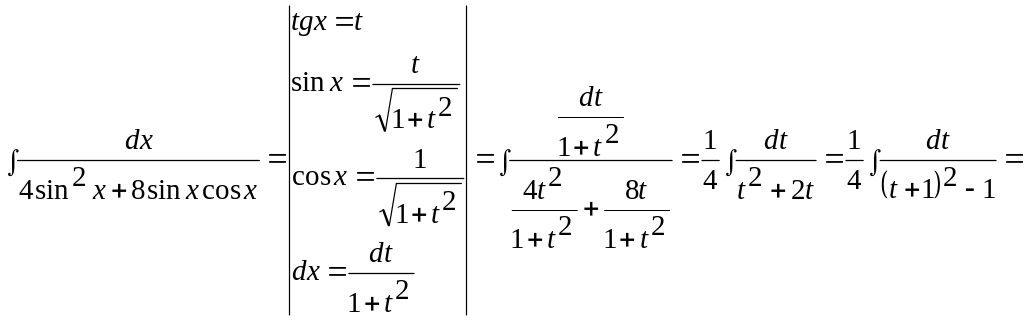
Интегралы видов
и
,
где
– целое положительное число, вычисляются
с помощью замены
или
и формул:
и
.
Пример 9.
.
Пример 10.
.
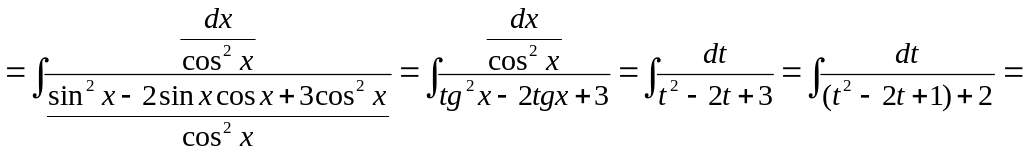
Пример 11.
.
§3. Определенный интеграл
3.1 Понятие определённого интеграла, его геометрический смысл
Пусть
функция
определена на отрезке
и
– произвольное разбиение этого отрезка
на
частей (рис.1).
Рис. 1
Сумма
,
где
,
,
называется интегральной
суммой для
функции
на отрезке
.
Геометрически
представляет собой алгебраическую
сумму площадей соответствующих
прямоугольников (см. рис.1).
Предел
суммы
при условии, что число разбиений
стремится к бесконечности, а наибольшая
из разностей
– к нулю, называется определенным
интегралом
функции
на отрезке
,
т.е.
.
Если
функция
непрерывна на
,
то она интегрируема на
,
то есть предел существует и не зависит
от способа разбиения промежутка
интегрирования
на частичные отрезки и от выбора точек
на этих отрезках. Геометрически
определенный интеграл представляет
собой алгебраическую сумму площадей
фигур, составляющих криволинейную
трапецию
,
в которой площади частей, расположенных
выше оси ОХ
, берутся со
знаком плюс, а площади частей, расположенных
ниже оси ОХ,
– со знаком
минус (см. рис.1).