Интегральное исчисление функций одной переменной

§1. Неопределенный интеграл: основные понятия

1.1 Понятие первообразной функции

Задача дифференциального исчисления сводится к нахождению по заданной функции ее производной. Неопределенный интеграл решает обратную задачу: по заданной производной находит первоначальную функцию.

Функция называется первообразной функции , заданной на некотором множестве , если для всех . Очевидно, что если , то и , где – постоянная величина, т.е. первообразная функция в случае существования определяется неоднозначно. С другой стороны, можно доказать, что функциями вида исчерпываются все первообразные от функции .

1.2 Неопределенный интеграл, его свойства

Если функция является первообразной для , то выражение называется неопределенным интегралом от функции и обозначается символом

,

где – знак интеграла,

– подынтегральное выражение,

– подынтегральная функция,

– первообразная функции ,

С – произвольная постоянная.

Отыскание неопределенного интеграла называется интегрированием функции. Для отыскания неопределенного интеграла используют таблицы основных интегралов, свойства интеграла (в частности, линейность), тождественные преобразования (так называемое непосредственное интегрирование), а также применяют различные специальные приемы, позволяющие привести исходные интегралы к табличным.

Свойства неопределенного интеграла:

1. .

2. .

3. .

4. .

5. .

6. Если , то .

1.3 Интегралы от основных элементарных функций

Из определения первообразной и неопределенного интеграла следует, что таблицу основных интегралов можно получить из таблицы основных производных, считая производные табличных функций подынтегральными функциями, а сами функции – их первообразными. Справедливость всех равенств легко проверить дифференцированием, т.е. установив, что производная от правой части равна подынтегральной функции.

1. 2.

3. 4)

5. 6.

7. 8.

9. 10.

11. 12.

13.

14.

15.

16.

Непосредственное интегрирование.

Непосредственное интегрирование основано на прямом использовании табличных интегралов, свойств и правил интегрирования. Рассмотрим несколько примеров непосредственного интегрирования.

Вычислить интегралы:

Пример 1.

.

Пример 2.

.

Пример 3.

.

Пример 4. .

Пример 5.

.

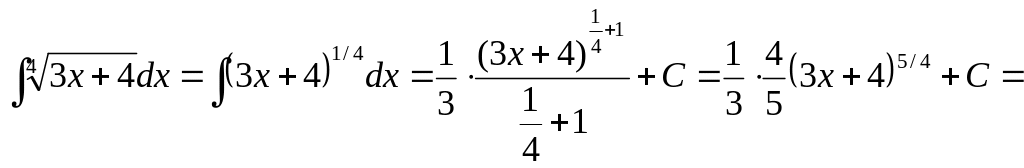
Пример 6.

.

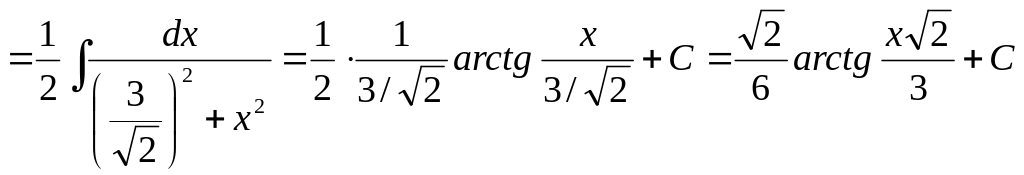§2. Методы интегрирования.

2.1 Интегрирование методом замены переменной (метод подстановки)

Этот метод используется в тех случаях, если нельзя непосредственно подобрать первообразную для подынтегральной функции . Метод подстановки состоит в следующем: в интеграле переменную заменяют новой переменной , связанной с формулой . Определив из этой формулы и подставив в интеграл, получим

.

Функцию выбирают таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид.

Пример1. .

Пример 2. .

Пример 3. .

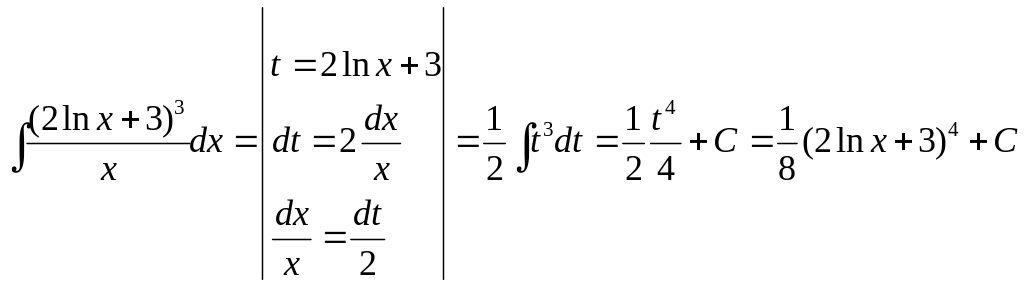Пример 4. .

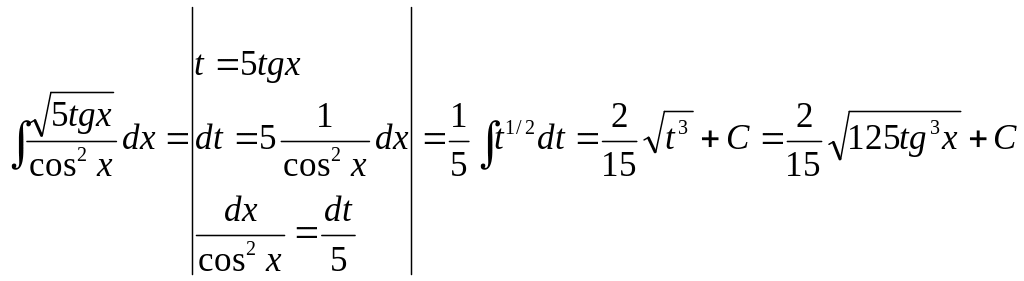Пример 5. .

Пример 6.

.

Пример 7.

.

Пример 8.