Базовые логические элементы "И", "ИЛИ", "НЕ"

Основой цифровой электроники являются логические элементы. На их основе состоят различные триггеры, дешифраторы, счётчики и т.д. Вот, к примеру, говорят же в процессоре миллионы транзисторов, но как их так собрали, ничего не перепутав и всё упорядочив? Из транзисторов собраны логические элементы, из логических элементов собраны различные счётчики, дешифраторы, триггеры, а из триггеров озу память и т.д. , а всё вместе в сборе получается , процессор.

----------------------<cut>----------------------

Компоненты процессора собраны в одном кристалле, но когда-то были громоздкие платы, выполняющие такую же функцию. Зная, как работают логические элементы, можно понять, как работают и все остальные цифровые микросхемы и научиться составлять самому схемы.

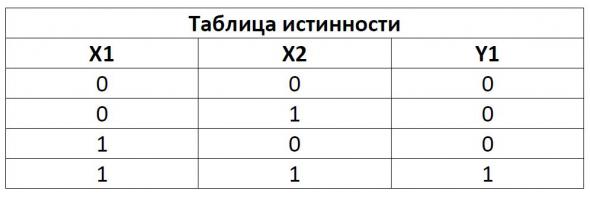
Элемент И

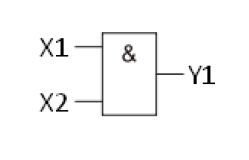Смысл элемента в том, чтобы получить на выходе логический уровень нужно подать на все входы логические единицы (в данном примере их только два, но бывает и больше), то есть И на 1 вход И на 2 вход. Если подать единицу только на один вход, из выхода не будет напряжение идти, будет логический ноль. Думаю по таблице истинности понять его работу нетрудно. На рисунке изображён элемент 2И, то есть у него 2 входа. Наши российские (и советские) микросхемы это все серии ЛИ, например К155ЛИ1 .

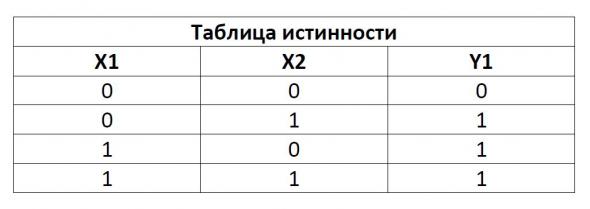
Элемент ИЛИ

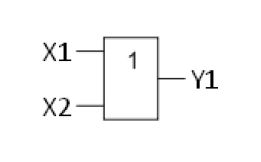
Чтобы на выходе появился логический уровень, нужно чтобы на любом входе ИЛИ на все входы подать логическую единицу. У элемента бывает более чем 2 входа, так же как и на элементе И. Элементы ИЛИ это микросхемы серии ЛЛ, например К155ЛЛ1 .

Элемент НЕ

Элемент НЕ выполняет роль инвертора. На выходе всегда логическая единица, пока на входе логический нуль и наоборот. Наши микросхемы это серии ЛН: К155ЛН1, К561ЛН2 и т.д.

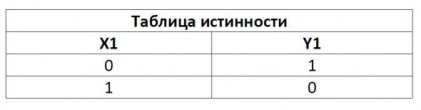
Исключающее ИЛИ

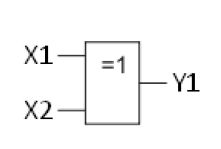
Этот логический элемент имеет необычный смысл работы: на выходе появится логический уровень в том случае, если только на одном из входов будет присутствовать логическая единица. Если на оба входа (или на все) подать одинаковые уровни, тогда на выходе уровень не изменится.

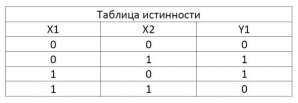
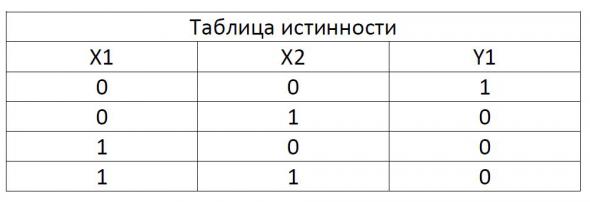
Элемент И-НЕ

Элемент имеет ту же функцию что и элемент И, но только сигнал на выходе инвертируется. Из таблицы смысл не трудно понять. Это микросхемы серии ЛА: К155ЛА3

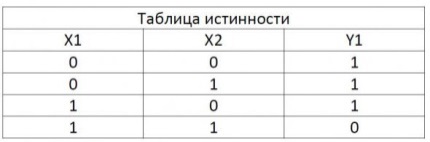
Элемент ИЛИ-НЕ

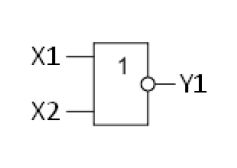
Этот элемент тоже имеет такую функцию, как и элемент ИЛИ. Микросхемы серии ЛЕ: К155ЛЕ1

Пример применения логических элементов RS-триггер

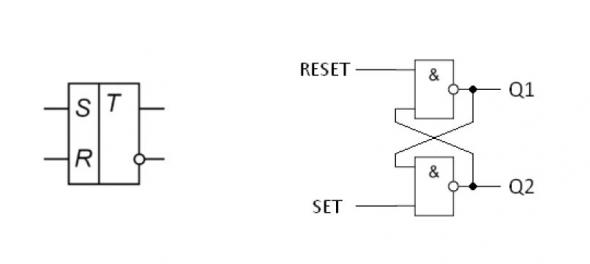
RS триггер – это устройство, которое может устойчиво сохранять одно из двух состояний, или можно сказать «ОЗУ на 1 бит». Q2 это инверсированный Q1 выход. SET установка, RESET сброс. При подаче логического сигнала на RESET, триггер обнуляется, т.е. на Q1 лог. уровень 0. Чтобы триггер перевести в состояние, где из Q1 выходит лог. 1, нужно в момент сброса установить на SET единицу. После прекращения подачи сигнала на RESET, триггер переходит в режим хранения, т.е. триггер запоминает состояние на входе SET.

Двоичные логические операции с цифровыми сигналами (битовые операции)[править | править исходный текст]

Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.

Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.

Из   возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.

Отрицание, не[править | править исходный текст]

Инвертор, НЕ

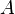
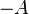
0	1
1	0

Мнемоническое правило для отрицания звучит так: На выходе будет:

• «1» тогда и только тогда, когда на входе «0»,

• «0» тогда и только тогда, когда на входе «1»

Повторение[править | править исходный текст]

Повторитель (буфер)

0	0
1	1

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из   возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция и[править | править исходный текст]

И

0	0	0
1	0	0
0	1	0
1	1	1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «1»,

• «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

Словесно эту операцию можно выразить следующим выражением: "Истина на выходе может быть при истине на входе 1 И истине на входе 2".

Дизъюнкция (логическое сложение). Операция или[править | править исходный текст]

ИЛИ

0	0	0
1	0	1
0	1	1
1	1	1

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,

• «0» тогда и только тогда, когда на всех входах действуют «0»

Инверсия функции конъюнкции. Операция и-не (штрих Шеффера)[править | править исходный текст]

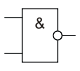
И-НЕ

0	0	1
0	1	1
1	0	1
1	1	0

Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,

• «0» тогда и только тогда, когда на всех входах действуют «1»