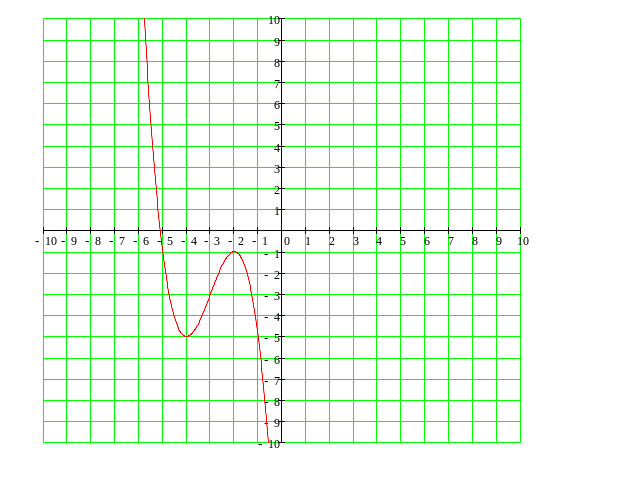
7. Исследовать методами дифференциального исчисления функцию и построить её графики:

у=-х³-9х²-24х-21.

1. Область определения D(у)=R, то есть функция непрерывна на всей числовой прямой, точек разрыва нет и, следовательно, нет вертикальных асимптот.

2. Так как область определения симметричное относительно х=0 множество, то будем исследовать функцию на чётность и нечётность:

у(-х)=-(-х)³-9(-х)²-24(-х)-21=х³-9х²+24х-21, так как у(-х)≠у(х) и у(-х)≠-у(х), то функция не является ни чётной, ни нечётной, а её график не симметричен ни относительно оси OY, ни относительно начала координат (0; 0).

3. у(х)ОY в точке (0; -21), так как при х=0  у=-21.

4. Вычислим первую производную функции:

у(х)=(-х³-9х²-24х-21)=-3х²-18х-24

у(х)=0  -3х²-18х-24=0  х²+6х+8=0  D=b²-4ac=6²-4∙1∙8=4

;

.

функция убывает на (-∞; -4] и на [-2; +∞); функция возрастает на [-4; -2]

x=-2 – точка max у=-1 – max, получили (-2; -1);

х=-4 – точка min y=-5 – min, получили (-4; -5).

5. Вычислим вторую производную функции:

y(х)=-6х-18

y(х)=0  -6х-18=0  х=-3

функция вогнута на (-∞; -3]; функция выпукла на [-3; +∞);

х=-3 – точка перегиба, получили (-3; -3).

6. y=kx+b – уравнение наклонной (горизонтальной) асимптоты, где

так как k=-∞, то функция не имеет ни наклонных, ни горизонтальных асимптот, то есть, никаких асимптот нет.

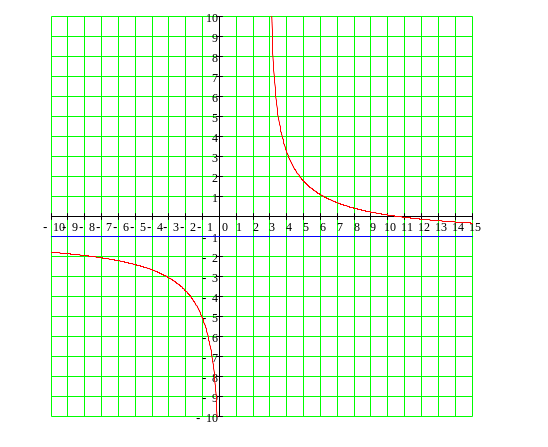
1. Область определения D(у)=(-∞; 1)(1; ∞), то есть функция непрерывна на своей области определения, х=1 - точка разрыва, исследуем поведение функции вокруг этой точки.

,

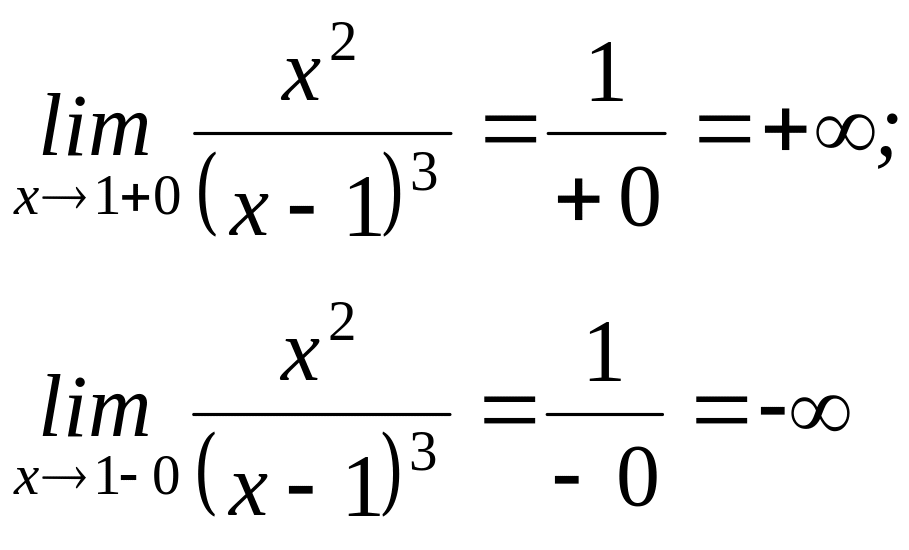следовательно, х=1 - вертикальная асимптота.

2. Так как область определения D(у) не симметричное относительно нуля множество, то функция не является ни чётной, ни нечётной, а её график не симметричен ни относительно оси OY, ни относительно начала координат (0; 0).

3. у(х)ОХ в точке (0; 0), так как при у=0 

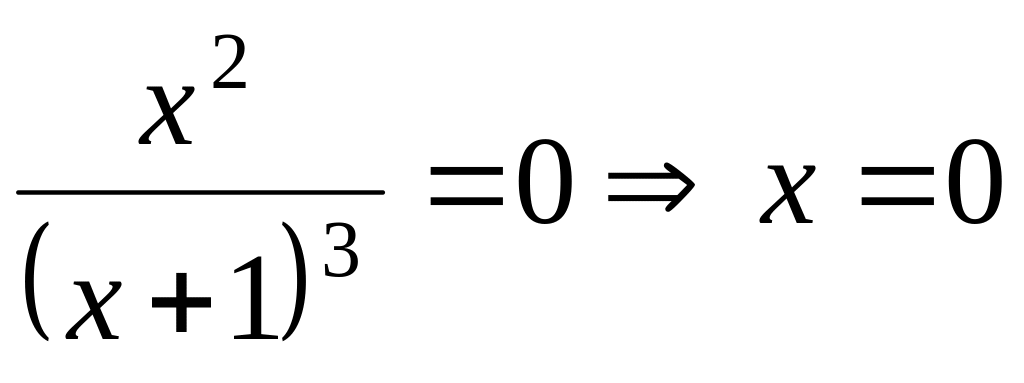
у(х) ОY в точке (0; 0), так как при x=0 

4. Вычислим у(х)

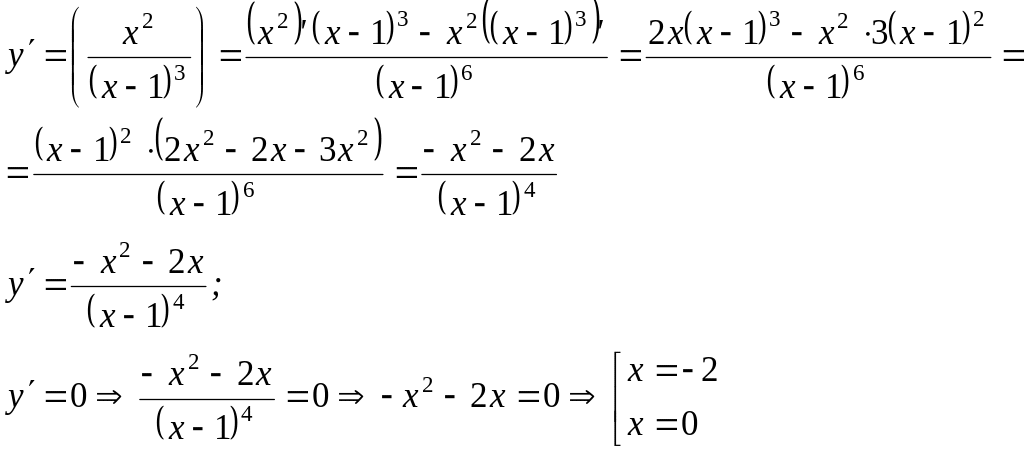
функция убывает на (-∞; -2], [0; 1) и на [-2; +∞);

функция возрастает на [-2; 0];

x=0 – точка max у=0 – max, получили (0; 0);

х=-2 – точка min y=-⁴/₂₇ – min, получили (-2; -⁴/₂₇).

5. Вычислим у(х)

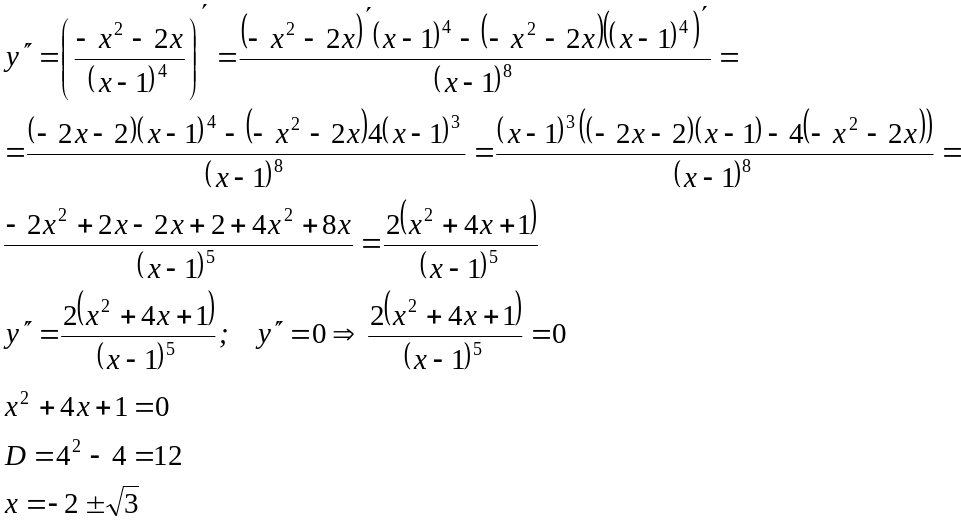
функция выпукла на (-∞; -2-√3]; [-2+√3; +∞);

функция вогнута на [-2-√3; -2+√3]; (1; +∞);

х=-2±√3 – точки перегиба;

получили

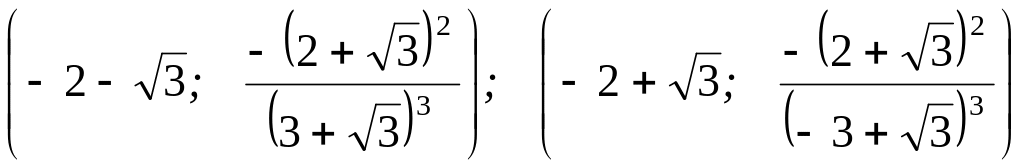
6. y=kx+b – уравнение наклонной (горизонтальной) асимптоты, где

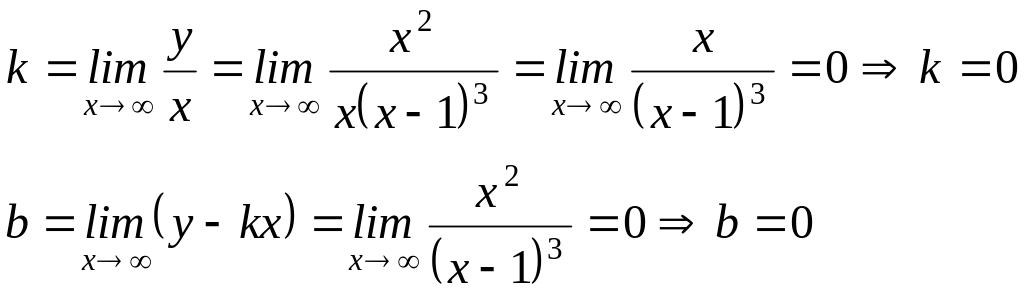
итак, у=0 – уравнение горизонтальной асимптоты.

1. Находим область определения:

, следовательно, область определения D(у)=(-∞; 0)(3; ∞), то есть х=0 и х=3 - граничные точки D(у), исследуем поведение функции на границе D(у).

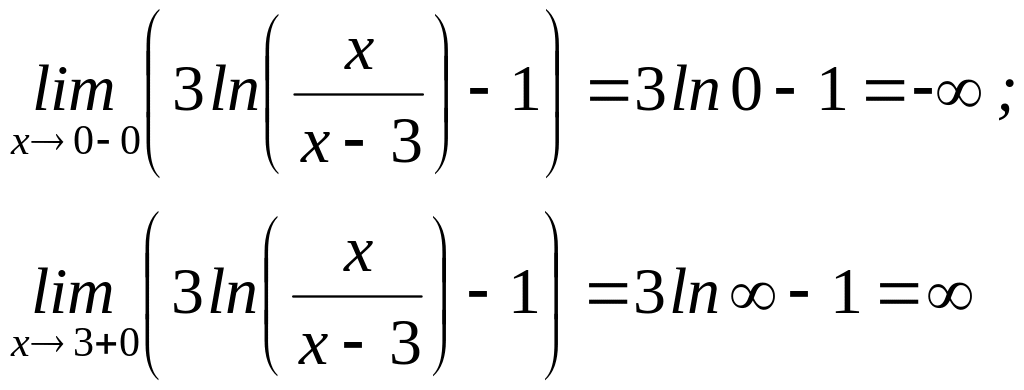
итак, х=0 и х=3 – вертикальные асимптоты.

2. Так как D(y) не симметрична относительно (0; 0), то эта функция не может быть ни чётной, ни нечётной, а её график не симметричен ни относительно оси OY, ни относительно начала координат (0; 0).

3. у(х)ОХ в точке (0; 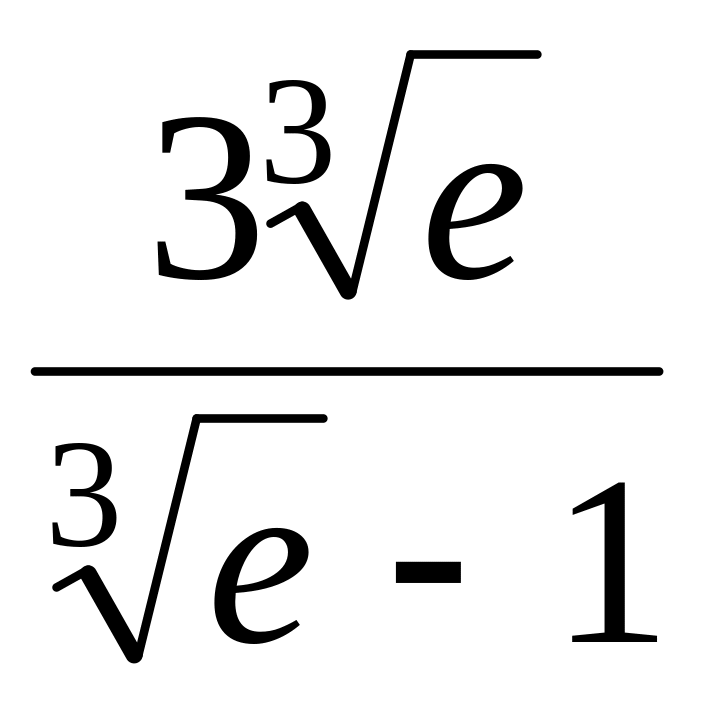), так как

у(х) ОY, так как х=0 D(y).

4. Вычислим у(х)

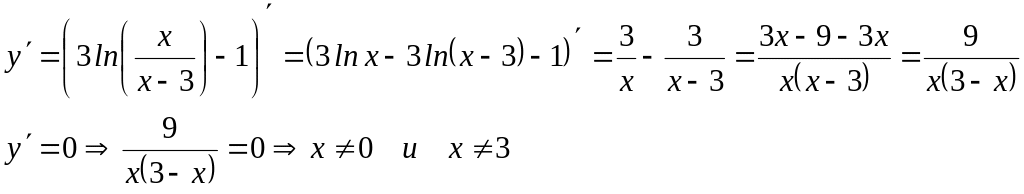
функция убывает на (-∞; 0); (3; +∞),

точек экстремума нет.

5. Вычислим у(х)

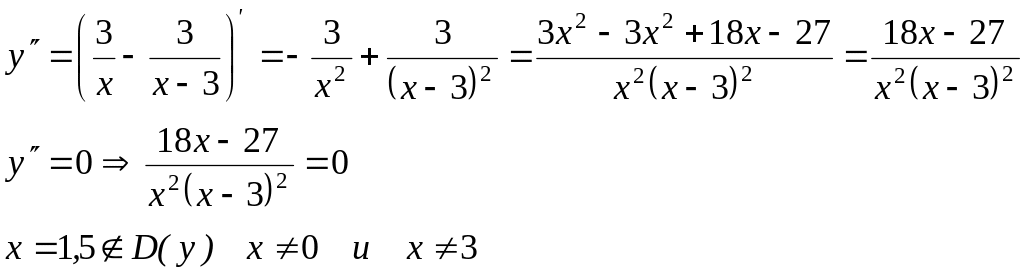
функция выпукла на (-∞; 0),

функция вогнута на (3; +∞);

точек перегиба нет;

6. y=kx+b – уравнение наклонной (горизонтальной) асимптоты, где

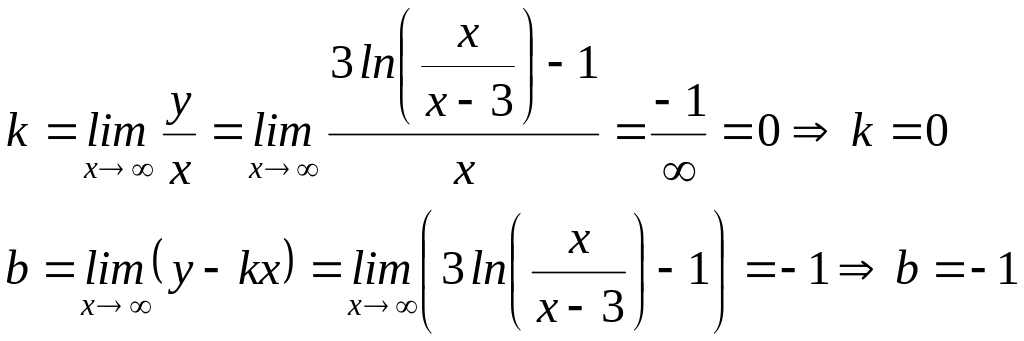
итак, у=-1 – уравнение горизонтальной асимптоты.