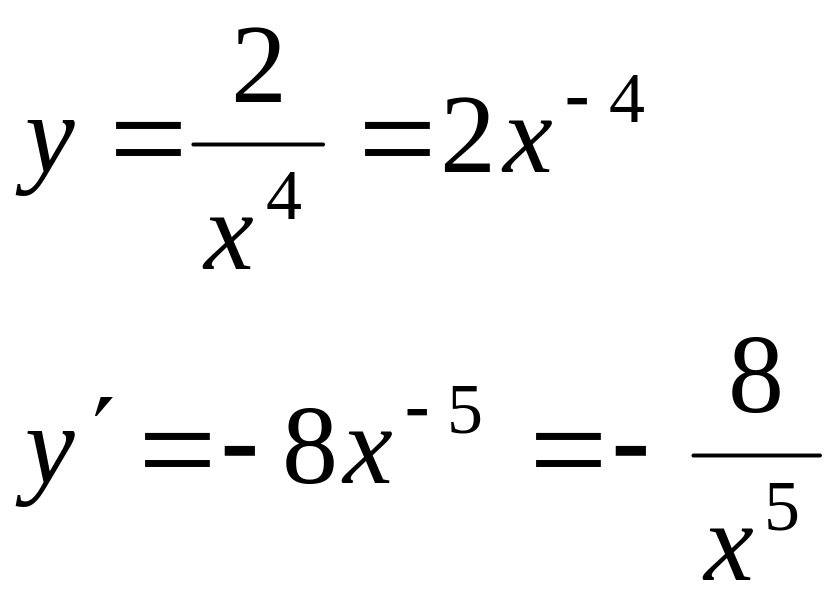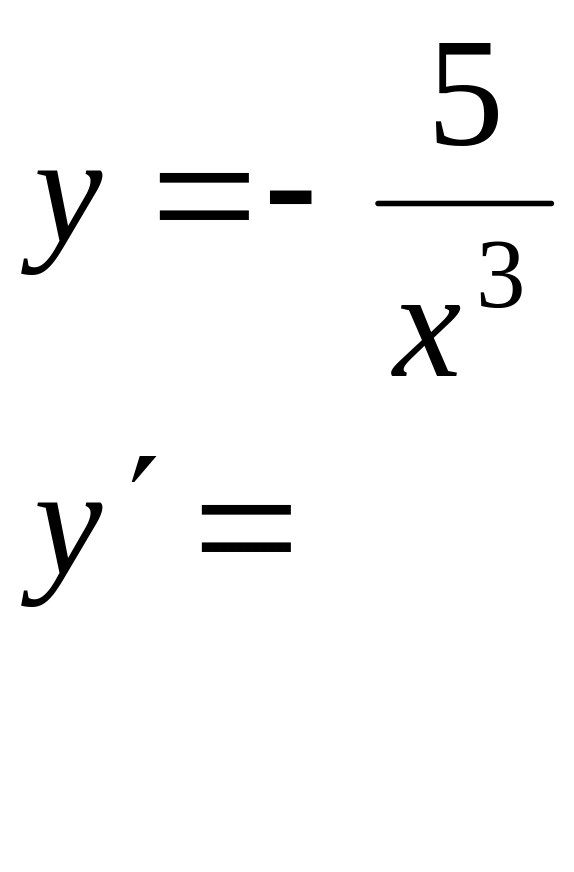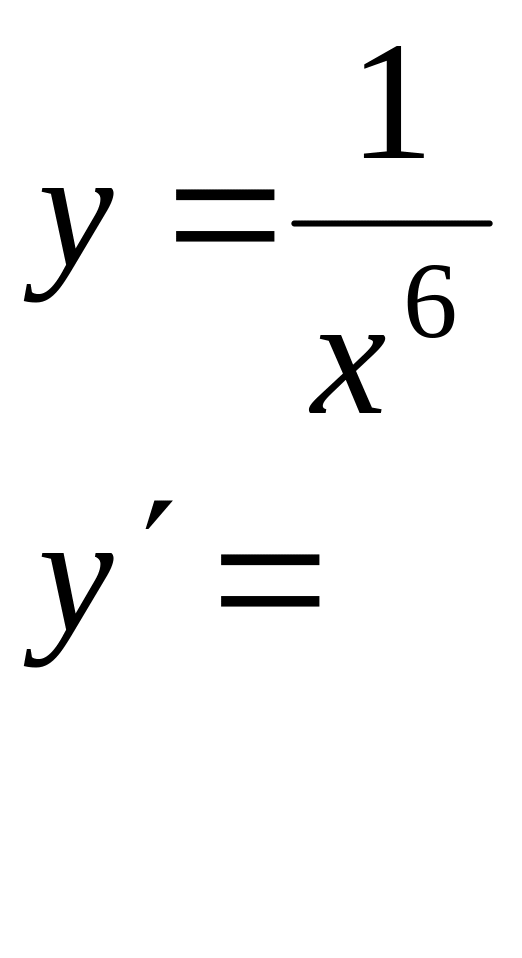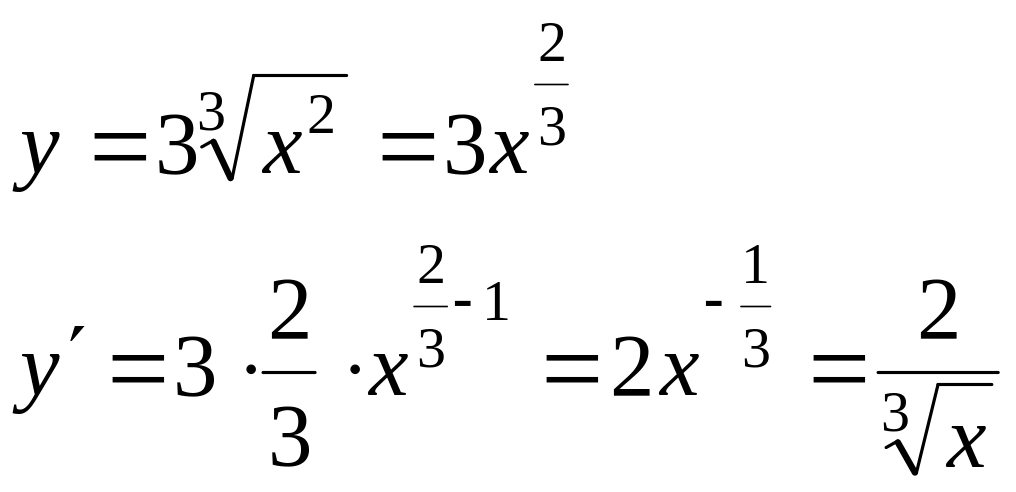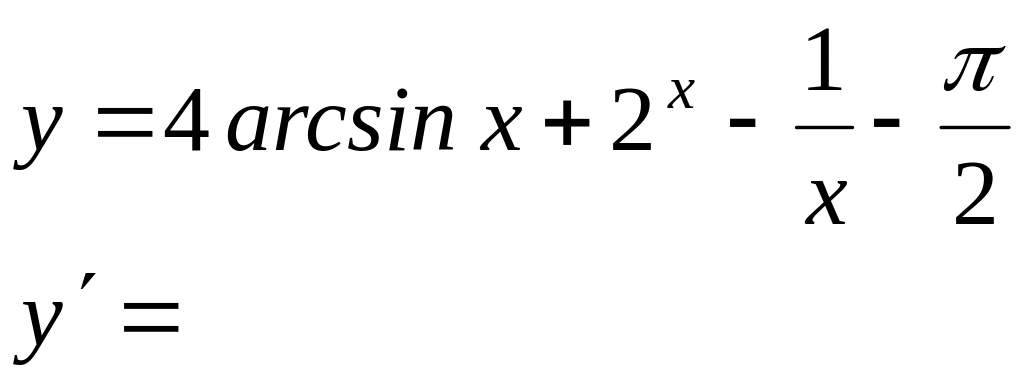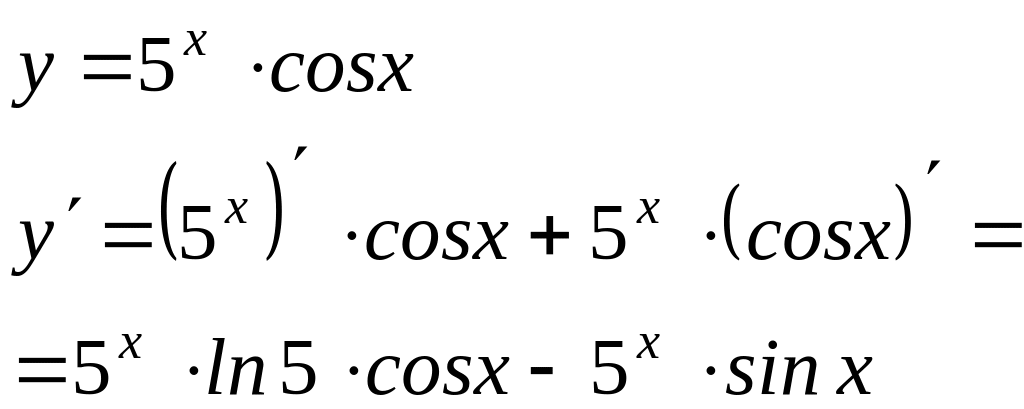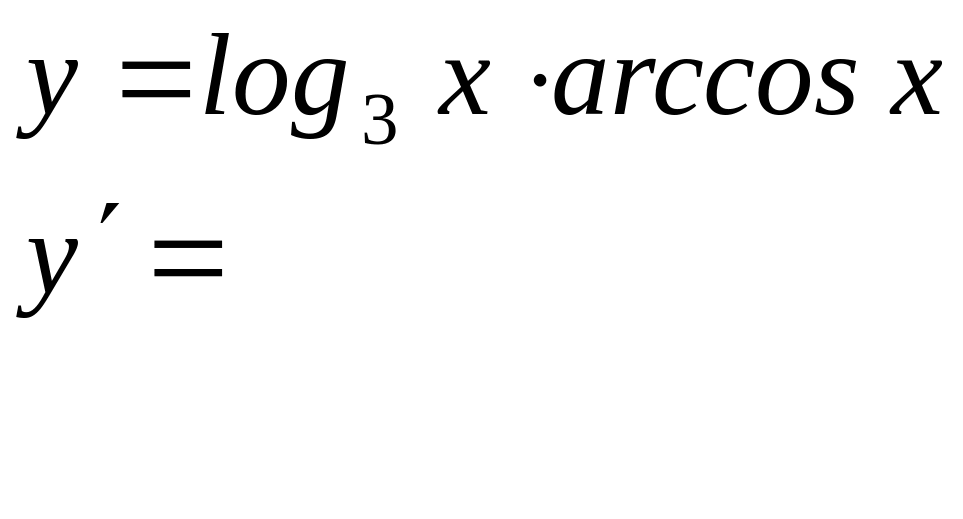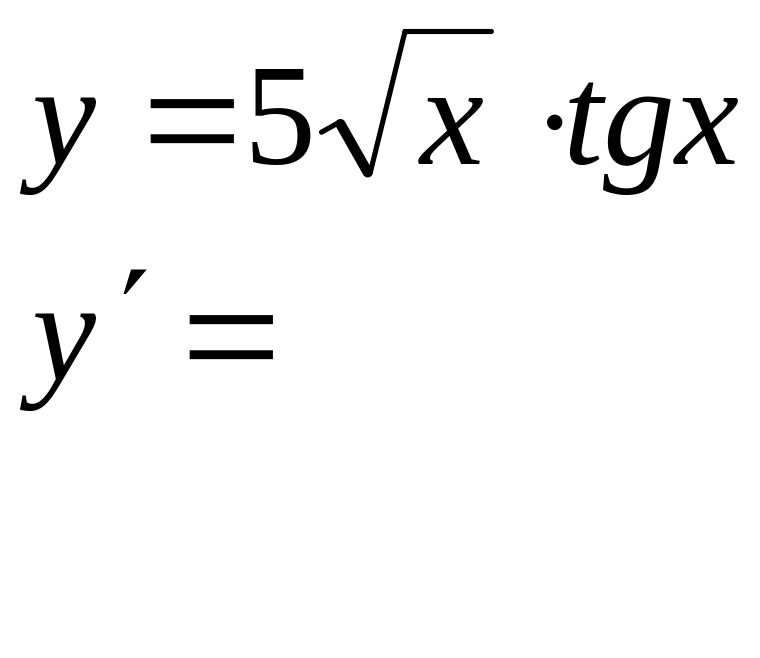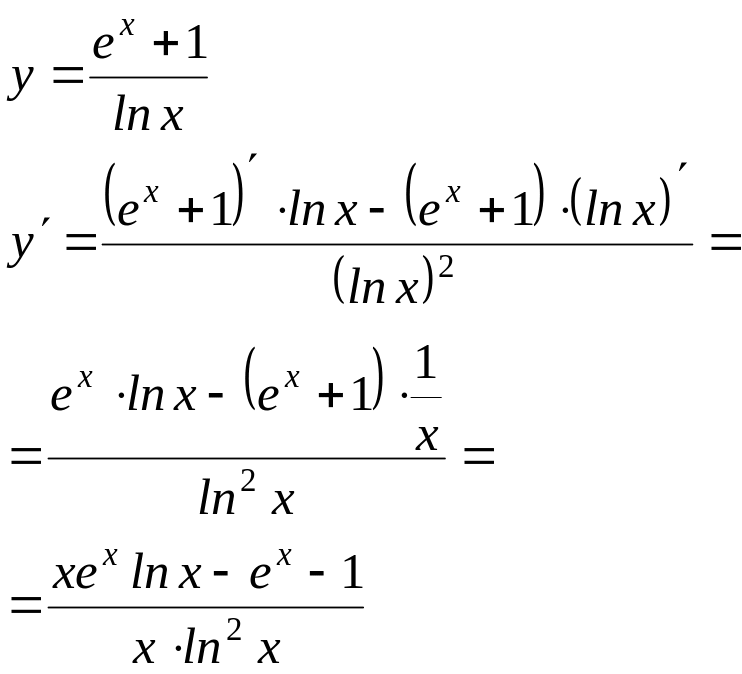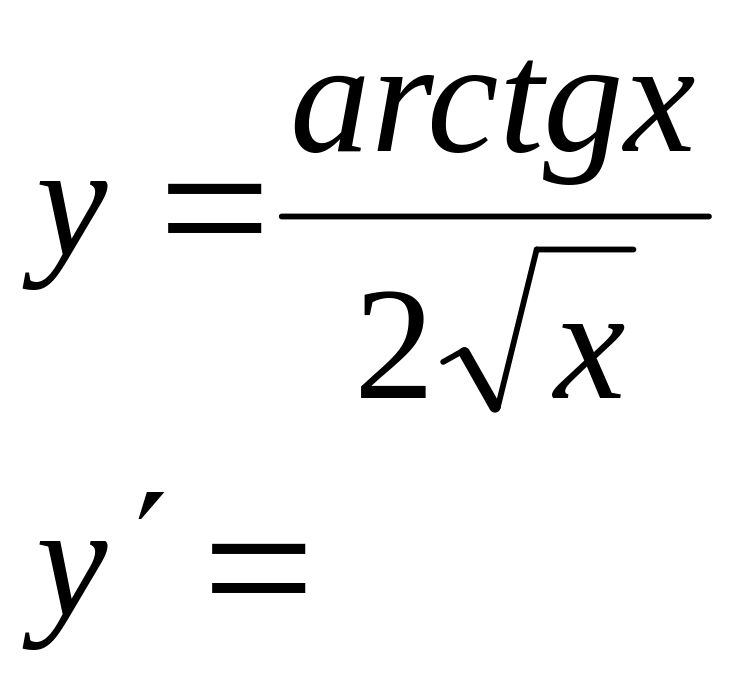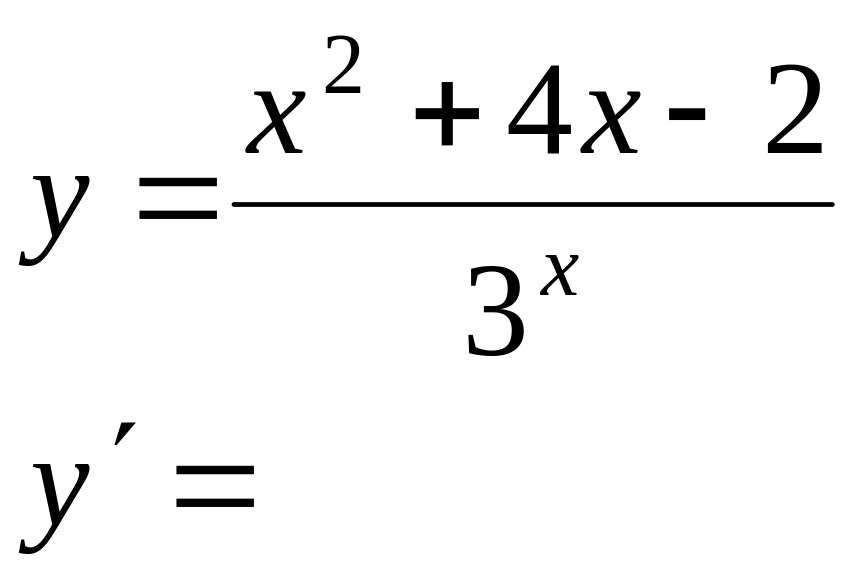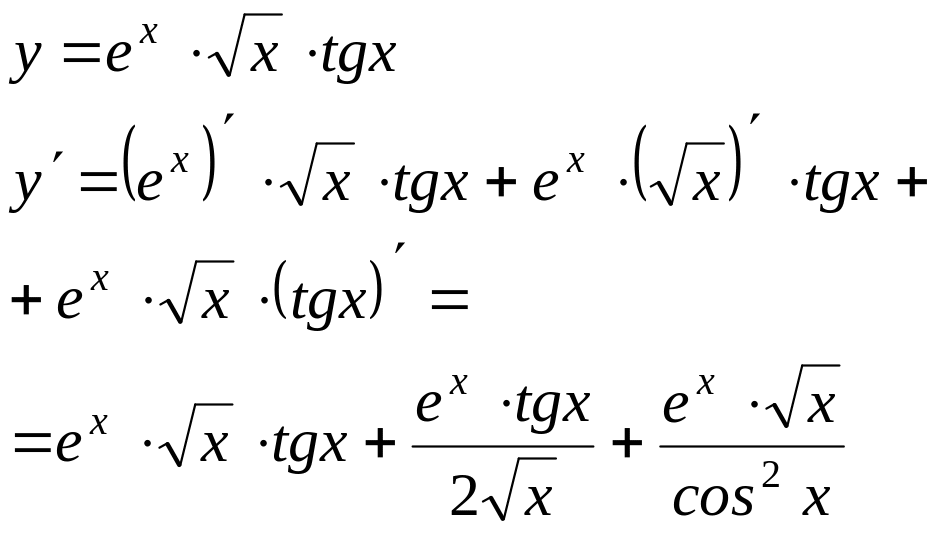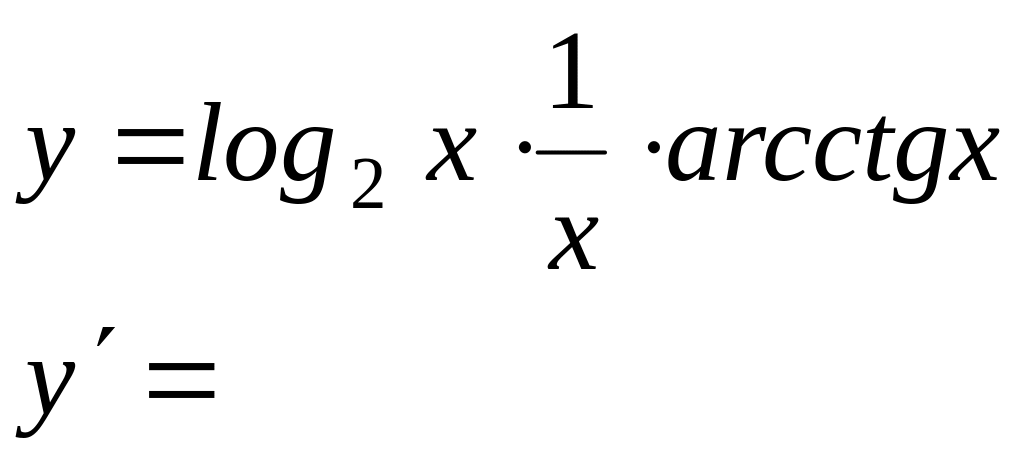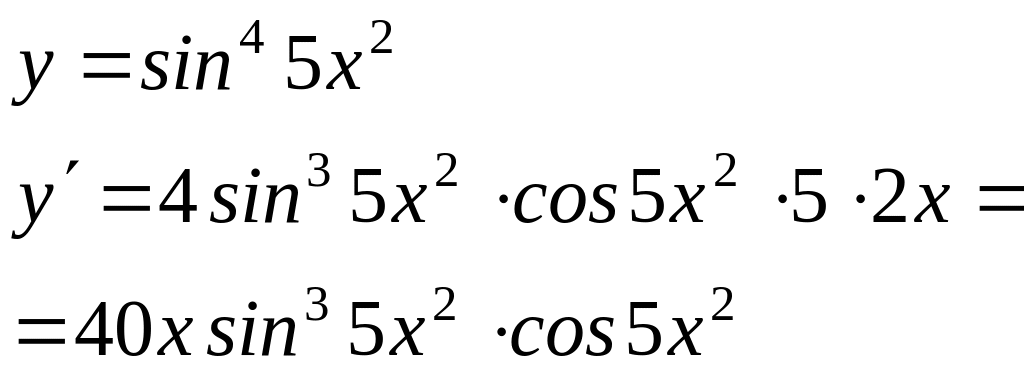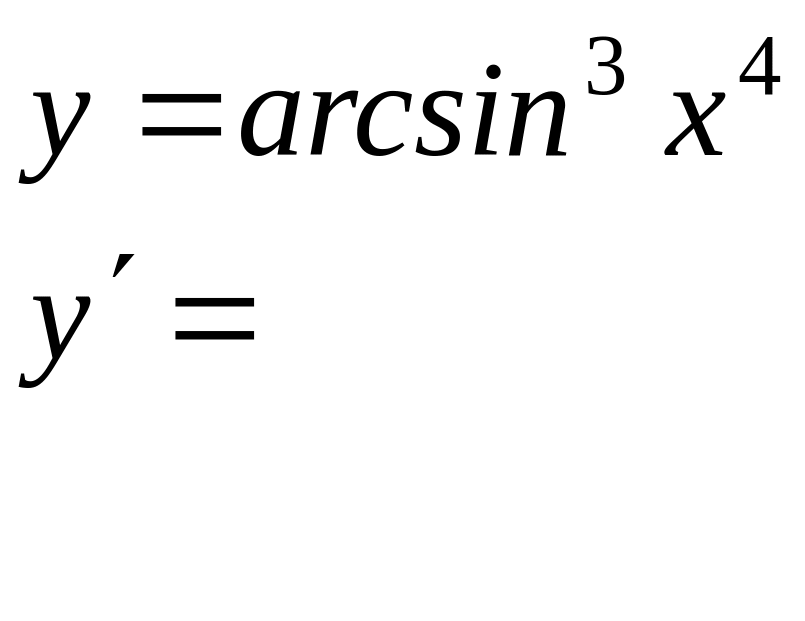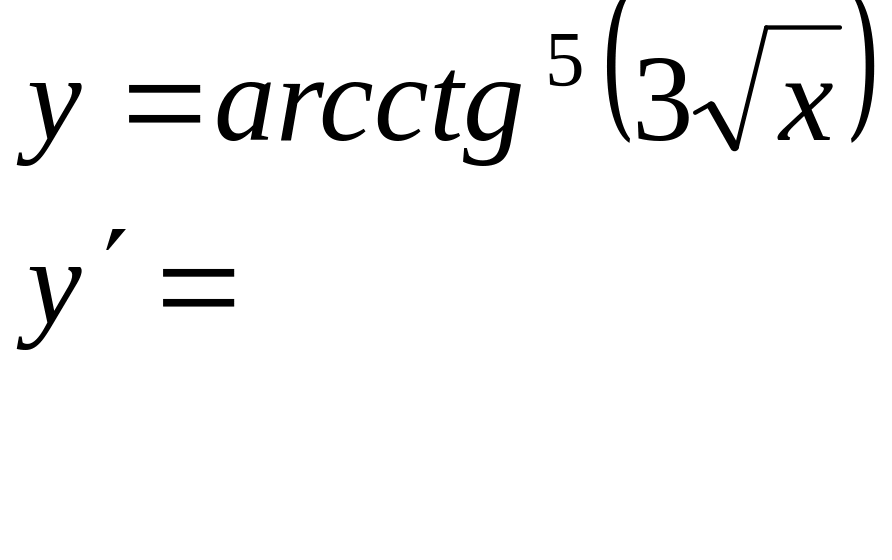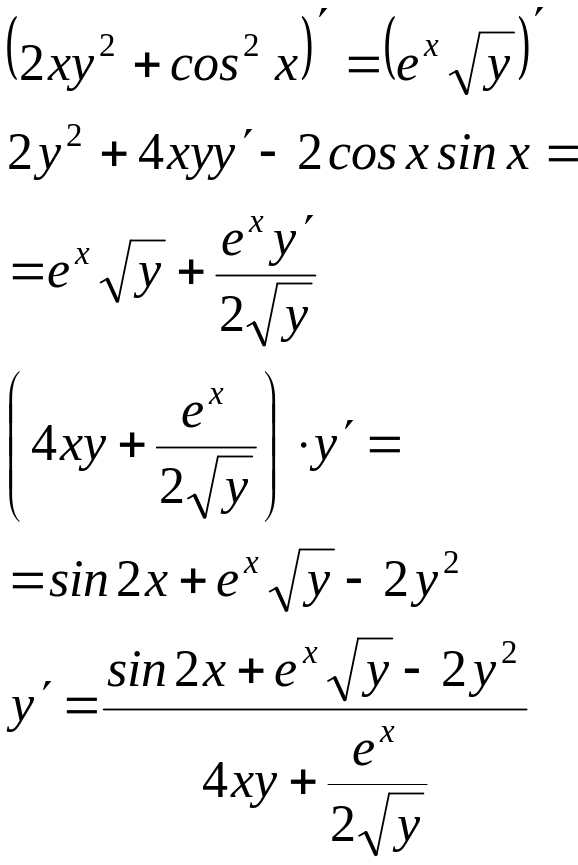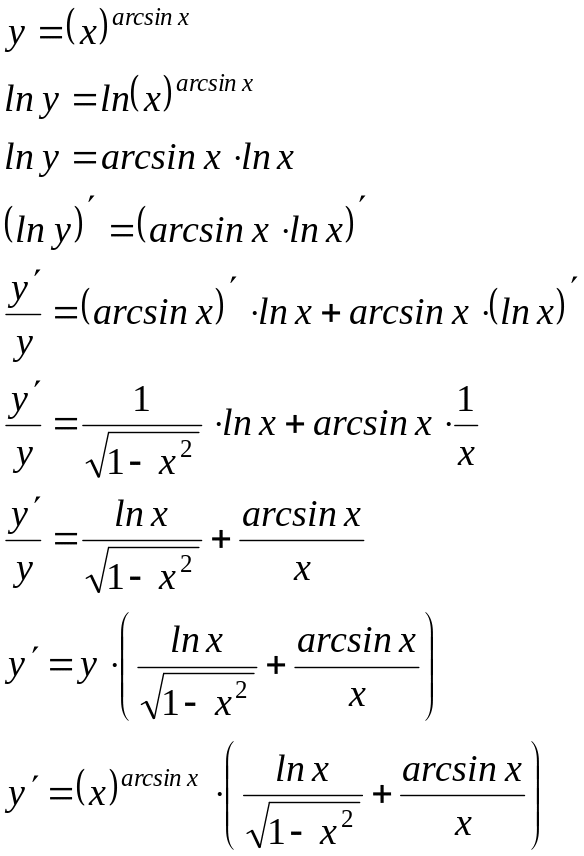Занятия 3-4 Производная функции и её применение.
Таблица производных и дифференциалов простейших элементарных функций.
Вид функции |
|
Производная
|
Дифференциал
|
Степенная |
|
|
|
Её следствия, или наиболее часто встречающиеся функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Показательная |
|
|
|
Экспоненциальная |
|
|
|
Логарифмическая |
|
|
|
|
|
|
|
|
Тригонометрические |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратные тригонометрические |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные правила нахождения производных.
|
Производная суммы есть сумма производных |
|
Производная разности есть разность производных |
( |
Производная произведения равна сумме произведений производной первого множителя на второй и первого множителя на производную второго |
|
Постоянный множитель можно выносить за знак производной. |
|
Производная дроби равна отношению разности произведений производной числителя на знаменатель и числителя на производную знаменателя к квадрату знаменателя |
)
где
С=cоnst
Дифференцирование сложной функции.
Если функция х=(t) имеет производную в точке t0, а функция y=f(x) имеет производную в соответствующей точке х0=(t0), то сложная функция f((t)) имеет производную в точке t0, и имеет место следующая формула:
y(t0)=f(x0)(t0).
Вычислить производные следующих функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить производные следующих сложных функций:
|
|
|
|
|
|
|
|
|
Вычислить производные следующих неявных функций:
|
|
|
Вычислить производные следующих функций, применяя логарифмическое дифференцирование:
Применим логарифмическое дифференцирование:
|
||
|
|
|
