
- •Методичні вказівки
- •"Логістика"
- •Методичні вказівки
- •"Логістика"
- •1 Загальні положення щодо виконання розрахункової роботи з дисципліни "логістика"
- •1.1 Мета розрахункової роботи і загальні вимоги до її виконання
- •1.2 Вибір варіанту розрахункової роботи
- •1.3 Порядок викладення матеріалу і оформлення розрахункової роботи
- •1.4 Порядок рецензування та захисту розрахункової роботи
- •2 Список рекомендованої літератури Основна література
- •Додаткова література
- •3 Завдання та методичні вказівки до виконання розрахункової роботи з дисципліни "логістика"
- •3.1 Завдання 1 "Прогнозування попиту на матеріальні ресурси методом екстраполяції" Загальні вказівки
- •Постановка задачі
- •Приклад розв'язання
- •Рішення
- •3.2 Завдання 2 "Розрахунок транспортних засобів перервної (циклічної) дії" Загальні вказівки
- •Постановка задачі
- •3.3 Завдання 3 "Раціональна організація вантажоперевезень" Загальні вказівки
- •Постановка задачі
- •Приклад розв’язання
- •3.4 Завдання 4 "Розрахунок площі складських приміщень " Загальні вказівки
- •3.5 Завдання 5 "Визначення оптимальної партії замовлення методом Уілсона" Загальні вказівки
- •Постановка задачі
- •Приклад розв’язання
- •3.6 Завдання 6 "Оптимізація величини логістичних витрат за допомогою авс аналізу" Загальні вказівки
- •Постановка задачі
- •Приклад розв’язання
- •3.7 Завдання 7 "Оптимізація розміщення розподільчих центрів" Загальні вказівки
- •Постановка завдання
- •Приклад розв’язання
- •Додаток в
- •Додаток г
- •Додаток д
- •Продовження табл. Д.1
- •Методичні вказівки
- •"Логістика"
1.4 Порядок рецензування та захисту розрахункової роботи
Після реєстрації на кафедрі оформлена розрахункова робота передається на рецензування викладачу. Під час рецензування визначаються відповідність структури та змісту розрахункової роботи завданню, правильність складання графіків та виконання розрахунків. Особлива увага під час рецензування приділяється наявності висновків та пропозицій щодо питань, які розглядаються.
Розрахункова робота повертається студенту на доопрацювання у таких випадках:
відсутності розділу, який передбачено структурою роботи;
невідповідності варіанту завдання змісту розрахункової роботи;
відсутності висновків;
невідповідності роботи вимогам цих методичних вказівок.
Після доопрацювання розрахункова робота повертається студентом на кафедру для рецензування. Результати рецензування "зараховано", "не зараховано", а також недоліки і переваги розрахункової роботи зазначаються викладачем у письмовій рецензії розрахункової роботи. Студент повинен ознайомитися з результатами рецензування.
2 Список рекомендованої літератури Основна література
Бажин И.И. Логистика: Компакт-учебник. – Харьков: Консум, 2003.
Гаджинский А.М. Основы логистики: Учеб. пособие. – М.: ИВЦ "Маркетинг", 1996.
Кальченко А.Г. Логістика: Підручник. – К.: КНЕУ, 2003.
Козловский В.А., Козловская Э.А., Савруков Н.Т. Логистический менеджмент. – СПб.: Политехника, 1999.
Крикавський Є.М. Логістика підприємства: Навч. посібник. – Львів: Львівська політехніка, 1996.
Крушельницька О.В. Управління матеріальними ресурсами: Навч. посібник. – К.: Кондор, 2003.
Логистика: Учеб. пособие / Под. ред. Б.А. Аникина. – М.: ИНФРА-М, 1997.
Логістика // Маркетинг у прикладах і завданнях: Навч. посібник / За заг. ред. С.М. Ілляшенка. – Суми: ВТД "Університетська книга", 2006.
Логістика // Маркетинг: бакалаврський курс: Навч. посібник / За заг. ред. С.М. Ілляшенка. – Суми: ВТД "Університетська книга", 2004.
Неруш Ю.М. Коммерческая логистика: Учебник для вузов. – М.: Банки и биржи, ЮНИТИ, 1997.
Додаткова література
Залманова М.Е. Сбытовая логистика: Учеб. пособие по курсу "Логистика". – Саратов: Саратовский гос. техн. ун-т, 1993.
Котлер Ф. Основы маркетинга. – М.: Прогресс, 1990.
Мате Э., Тиксье Д. Материально–техническое обеспечение деятельности предприятия. – М.: А/О Изд. группа "Прогресс", 1993.
Сергеев В.И. Менеджмент в бизнес - логистике. – М.: Филинъ, 1997.
Смехов А.А. Основы транспортной логистики. – М.: Транспорт, 1995.
Фатхутдинов Р.А. Организация производства: Учебник. – М.: ИНФРА-М, 2001.
Фирон Х., Линдерс М. Управление снабжением и запасами. Логистика / Пер. с англ. – СПб.: Полигон, 1999.
3 Завдання та методичні вказівки до виконання розрахункової роботи з дисципліни "логістика"
3.1 Завдання 1 "Прогнозування попиту на матеріальні ресурси методом екстраполяції" Загальні вказівки
Важливе місце в методичному забезпеченні визначення перспективної потреби підприємств в матеріальних ресурсах займають економіко - статистичні методи. При прогнозуванні потреби в матеріальних ресурсах можуть використовуватися такі методи як: метод кореляційного аналізу (виявлення зв'язку між потребою в ресурсах і факторами що визначають цю потребу), методи експертних оцінок, нормативний метод, метод регресійного аналізу (метод екстраполяції).
Основна ідея методу екстраполяції базується на використанні факту інерційності економічних процесів - достатньо виявити основну тенденцію розвитку явища в часі (тренд), а потім використати її для розробки прогнозу. Метод екстраполяції дає позитивні результати на найближчу перспективу прогнозування тих чи інших процесів - на 5-7 років.
Операцію екстраполяції в загальному вигляді можна уявити собі як визначення значень функції:
X = f (t), (3.1.1)
де X - потреба в матеріальних ресурсах; t - час.
Функціональна залежність віднаходиться таким чином. Задається вид функціональної залежності, наприклад лінійна залежність х*= а0+а1t або квадратична х*= а0+а1t+а2t2 для функції однієї змінної. Вибрану залежність підставляють в наступну функцію, що підлягає мінімізації, наприклад:
![]() (3.1.2)
(3.1.2)
де j – кількість спостережень змін x у часі.
В
цієї функції розраховується квадрат
відхилення значень аналітичної кривої
регресії від значень
![]() .
Диференціюючи за коефіцієнтами рівняння
регресії та прирівнюючи одержані
значення до нуля, одержуємо систему
рівнянь, за якими легко знайти коефіцієнти
регресійної функції. Описаний метод
називається методом найменших
квадратів, тому
що він забезпечує мінімум суми квадратів
відхилень
.
Диференціюючи за коефіцієнтами рівняння
регресії та прирівнюючи одержані
значення до нуля, одержуємо систему
рівнянь, за якими легко знайти коефіцієнти
регресійної функції. Описаний метод
називається методом найменших
квадратів, тому
що він забезпечує мінімум суми квадратів
відхилень
![]()
![]() для всіх
для всіх
![]() .
.
![]()
Для
лінійної функції після диференціювання
по
![]() та
та
![]() ,
одержуємо систему із двох рівнянь:
,
одержуємо систему із двох рівнянь:
![]()
 (3.1.3)
(3.1.3)
![]()
Для квадратичної функції після диференціювання по та , одержуємо систему із трьох рівнянь:
![]()
 ,
,
![]() ,
(3.1.4)
,
(3.1.4)
![]() ,
,
Похибка прогнозу оцінюється шляхом обчислення остаточного середньоквадратичного відхилення.
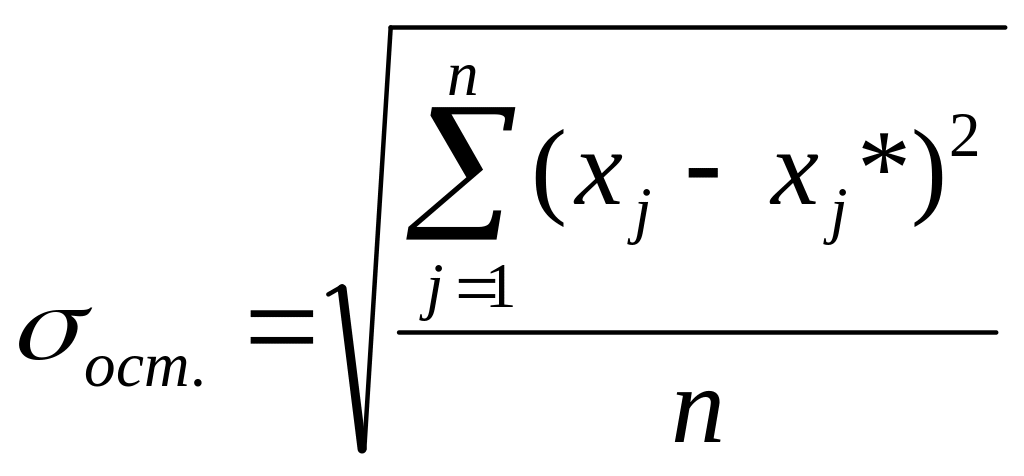 . (3.1.5)
. (3.1.5)
