- •Тема 1. Функция – зависимость между числовыми величинами, при которой аргументу функции ставится в соответствие одно и только одно значение функции.
- •Тема 3. . Постановка и классификация задач мп.
- •Тема 2. Метод множителей Лагранжа решения змп.
- •Тема 4. Геометрическое решение задач математического программирования.
- •Тема 5. Модель поведения потребителя.
- •Тема 7. Метод искусственного базиса и основы теории двойственности.
- •Тема 8. Постановка и основные понятия транспортной задачи.
- •Тема 6.
- •2) Находим начальное опорное решение.
Тема 1. Функция – зависимость между числовыми величинами, при которой аргументу функции ставится в соответствие одно и только одно значение функции.
Важнейшая характеристика функции – скорость её изменения – определяется значением её производной. Производная показывает, как изменится исследуемая нами величина, при небольшом изменении переменных, от которых она зависит.
Производная
функции
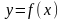 равна конечному пределу отношения
приращения функции
равна конечному пределу отношения
приращения функции
к
приращению аргумента, когда оно
стремиться к 0.


Функция возрастает, если большему значению аргумента соответствует большее значение функции.
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Признаки
монотонности Функция
возрастает
на
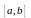 тогда
и только тогда, когда
тогда
и только тогда, когда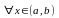
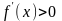 .
.
Функция
убывает
на
,
тогда и только тогда, когда
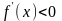
( Функция возрастает - производная положительна, функция убывает - производная отрицательна).–
Определения экстремумов |
Точка
|
Точка
-локальный
минимум,
если
|
|
Необходимое условие экстремума |
Если в точке функция достигает экстремума, то её производная в этой точке равна 0 или не существует. |
||
Достаточные
условия экстремума
|
Первое Если в любой точке окрестности слева от неё производная функции положительна, а справа – отрицательна, то - локальный максимум функции. А если производная при переходе через меняет знак с «-» на «+», то - локальный минимум. |
Второе Если в точке первая производная равна 0, а вторая производная отрицательна, то - локальный максимум функции. Если в точке первая производная равна 0, а вторая производная положительна ,то - локальный минимум функции. |
|
Частные производные функции двух переменных.
Частной
производной по х от функции
 называется
производная по х, вычисленная в
предположении, что у – постоянная, а
частной производной по у от функции
называется
производная по у, вычисленная в
предположении, что х – постоянная.
называется
производная по х, вычисленная в
предположении, что у – постоянная, а
частной производной по у от функции
называется
производная по у, вычисленная в
предположении, что х – постоянная.
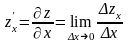 ;
;

Вектор
градиент.
Вектор,
координаты которого равны частным
производным функции
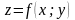 ,
называется вектором градиентом этой
функции.
,
называется вектором градиентом этой
функции.
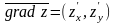 .
.
Определение локального экстремума функции нескольких переменных. Функция имеет локальный максимум в точке М0(х0,у0), если значении функции в этой точке больше, чем её значение в любой другой точке М(х,у) некоторой окрестности точки М0
(Точка
М0
– максимум,
если
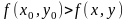 для
любых точек её окрестности.)
для
любых точек её окрестности.)
Точка
М0
– минимум,
если
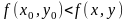 для
любых точек её окрестности.
для
любых точек её окрестности.
.Необходимое и достаточное условие существования экстремума для функции двух переменных.
Необходимое: Если функция достигает экстремума в точке М0(х0,у0), то все её первые частные производные в этой точке равны нулю или не существуют.
Достаточное:
Пусть в
некоторой окрестности точки М0(х0,у0)
функция
имеет непрерывные частные производные,
равные нулю в этой точке, тогда, если
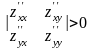 ,
то М0(х0,у0)
– является экстремумом функции
,
то М0(х0,у0)
– является экстремумом функции
 ,
причём, если
,
причём, если
 ,
точка М0
– минимум, если
,
точка М0
– минимум, если
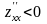 ,
точка М0
– максимум.
,
точка М0
– максимум.

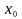 -локальный
максимум,
если для всех точек «около»
выполняется :
-локальный
максимум,
если для всех точек «около»
выполняется :
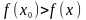
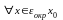 (эпсилон
- окрестности)
:
(эпсилон
- окрестности)
: