Лекція 4 «Метод згладжування і сезонне прогнозування»

Анотація

Наївна модель. Способи усунення тренда. Моделі згладжування для часових рядів, що не мають тренда: модель ковзного середнього, модель експоненційно зваженого ковзного середнього, комбінована модель. Визначення початкових значень моделі. Моделі згладжування з трендом: модель Холта, модель Брауна. Сезонні моделі.

4.1 Наївна модель

Зараз ми розглянемо найпростішу модель, яка коли-небудь використовувалася при прогнозуванні, – так звану «наївну модель». Значення моделі задаються наступною формулою:

(4.1)

Ідея наївної моделі (4.1) полягає в припущенні, що дане значення у момент часу t приблизно рівне попередньому значенню.

Стовпець значень Y_t виходить з початкових даних просто зрушенням на один рядок вниз. На рис. 4.1 представлений графік цієї наївної моделі, який виходить відповідно з початкового графіка шляхом зрушення на одиницю управо. Прогноз для всіх кварталів, починаючи з 18-го, один і той же і рівний останньому значенню ряду даних: 248.

Рисунок 4.1 – Графік наївної моделі

Наївна модель застосовується в тих випадках, коли потрібно зробити короткостроковий прогноз, за умови, що не очікується великих змін в характері процесу. Важливість цієї моделі для прогнозування в першу чергу полягає у тому, що разом з лінійною моделлю і моделлю постійного зростання наївна модель служить мірилом для визначення ефективності будь-якої іншої моделі. На практиці це означає, що, перш ніж придбати яку-небудь нову модель, треба порівняти її характеристики з їх аналогами.

4.2 Способи усунення тренда

Якщо уважно подивитися на графік наївної моделі (рис. 4.1), то помітите, що крім зрушення на одиницю управо він в більшій своїй частині (у 5 випадках з 16) розташований нижче за початкову криву. Це пов'язано з тим, що наївна модель (див. формулу 4.1) не припускає існування у процесу лінійного тренда. Тобто наївна модель виявиться неефективною, якщо значення коефіцієнта b₂ в лінійному рівнянні регресії значно відрізнятиметься від нуля. Існує досить багато інших моделей, набагато складніших, ніж наївна, які також припускають, що процес не має тренда. Як показник відсутності тренда у ряду Y_iіноді береться коефіцієнт k:

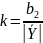(4.2)

Залишки лінійного рівняння регресії звичайно служать прикладом процесу, що не має лінійного тренда. Як правило, в бізнесі ми маємо справу з процесами, що мають тренд. Для того, щоб в цьому випадку можна було застосувати модель, призначену для процесів, що не мають тренда, можна поступити одним з наступних двох способів.

Спосіб 1. Розглянемо різниці або частки початкових даних. Таким чином, якщо є ряд даних Y₁, Y₂, ..., Y_n, то розглядається ряд: Δ2_{, ...,}Δn, де Δt = Y_t – Y_t-1, або ряд р2, ..., рn, де

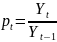(4.3)

Насправді прогнозисти звичайно поступають трохи інакше. До результатного ряду даних застосовується оператор ln. Toбто розглядається ряд: lnY₁, …, lnY_n, після чого до нього застосовується оператор приросту Δ. При значеннях р_i, близьких до одиниці, можна нехтувати другим членом в розкладанні Тейлора і вважати, що ln(p_t) ≈ p_t - 1.

Так як ln(p_t) = ln(1) + (ln(p_t))(p_t-1) + (ln(p_t))/2!*(p_t-1)²≈ 0 + 1/p_t*(p_t-1) = 0 + 1*(p_t-1) =p_t -1

Оператори Δ_i і р_i називають операторами початкового ряду. При цьому абсолютно не гарантовано, що ряди даних, одержані шляхом застосування операторів Δ_i або р_i, не матимуть тренда (У такому разі іноді застосовують повторно оператор Δ).

На рис. 4.2 представлене графічне зображення ряду р2,..., рn.

Рисунок 4.2 – Темпи зростання об'єму продажів

Якщо менеджер вважає, що можна нехтувати зміною в змодельованих квартальних темпах зростання, то він може розглядати р2, ..., рn як ряд, що не має тренда, і застосувати до нього наївну або будь-яку іншу модель, призначену для рядів, що не мають тренда.

Спосіб 2 полягає в розгляді залишків лінійної регресії і є одним з найчастіше використовуваних методів усунення тренда. Його називають методом детрендалізації.

Якщо коефіцієнт b2 лінійного рівняння регресії для ряду еiмає нулі в перших чотирьох десяткових розрядах, то він може вважатися рівним нулю. Тепер можна побудувати модель для ряду без тренда для залишків е_і, потім знайти відповідне змодельоване значення e_k при k > 17, і додати його до відповідного значення тренда. Оскільки наївна модель припускає, що e_t-1 ≈ e_t, то її слід застосовувати у тому випадку, коли коефіцієнт кореляції r(e_t-1, e_t ) при t = 2, ..., n, позитивний і значно відрізняється від нуля. У такому разі говорять, що в моделі лінійної регресії є позитивна автокореляція першого порядку. Існує спеціальний тест (тестДарбіна-Уотсона) на наявність автокореляції першого порядку.

Прогноз визначається шляхом додавання змодельованої помилки е₁₉ до відповідного значення тренда.