Код Хэмминга

Код Хэмминга предназначен для исправления одиночных ошибок и имеет кодовое расстояние d_min=3. Значения n и k кодов Хэмминга связаны соотношением 2^n-k-1=n . Строки проверочной матрицы Н представляют собой различные ненулевые последовательности длины (n-k). Изначально правила формирования проверочных элементов выбирались (50-е годы) так, чтобы результат контрольных сумм при приеме указывал порядковый номер искаженного элемента.

Пусть a_i – информационные символы, b_i – проверочные символы. Если проверочные символы разместить в кодовой комбинации на позициях, номера которых являются степенью двойки (1, 2, 4, 8 и т.д.), то получаемый синдром в двоичном виде указывает на номер искаженного элемента. Рассмотрим это на примере кода (7,4).

Правило формирования проверочных символов заключается в следующем: значение любого информационного символа должно быть равно сумме по модулю 2 тех проверочных символов, порядковые номера которых входят в разложение по степеням двойки порядкового номера данного информационного символа.

b₁ b₂ a₃ b₄ a₅ a₆ a₇

Р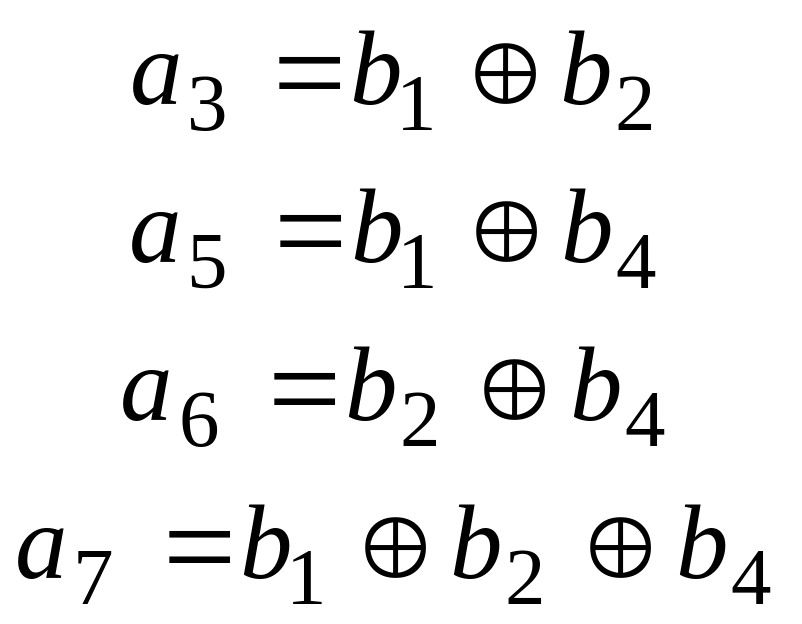 ешим эту систему уравнений относительно b₁, b₂ и b₄.

Т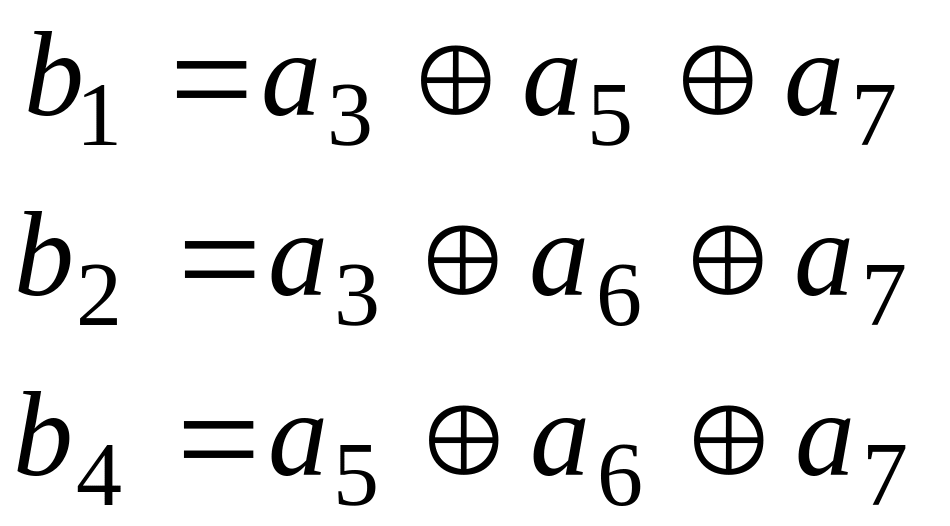 огда элементы синдрома S=(s₂,s₁,s₀) равны

Н апример, если ошибка произошла в символе a₃ , синдром будет иметь следующий вид S=(011), что означает десятичное число 3.

№7

Циклические коды

Циклическим кодом называется такой линейный код, у которого при любом циклическом сдвиге разрешенного кодового слова получается другое разрешенное кодовое слово.

Циклический код обладает всеми свойствами линейных кодов. Следовательно, его можно задать порождающей или проверочной матрицей. Но циклические коды обладают свойствами, которые позволяют сильно упростить процедуры и устройства кодирования и декодирования.

Представление кодовых слов степенными полиномами.

К одовые слова циклического кода ставят в соответствие степенным полиномам по следующему правилу: двоичной последовательности V длины n

с оответствует полином (n-1)-й степени

Здесь х – формальная переменная.

Циклический сдвиг кодового слова на i разрядов влево соответствует умножению полинома V(x) на xⁱ по модулю (xⁿ+1).

Пример.

Пусть n=7. Задано кодовое слово 1001101  x⁶+x³+x²+1. Сдвиг кодового слова на 1 разряд влево дает другое кодовое слово 0011011  х⁴+х³+х+1.

V(x)*xⁱ mod (xⁿ+1)=(x⁶+x³+x²+1)*x mod (x⁷+1)=(x⁷+x⁴+x³+x) mod (x⁷+1)= =x⁴+x³+x+1

A=BmodC (А равно остатку от деления В на С)

Циклический сдвиг кодового слова на i разрядов вправо соответствует умножению полинома V(x) на x^-i или х^n-i по модулю (xⁿ+1).

V(x)*x^-i mod (xⁿ+1)= V(x)*x^n-i mod (xⁿ+1)

Порождающий полином циклического кода

Множество кодовых слов циклического кода можно указать, задав любое ненулевое кодовое слово. Обычно для задания циклического кода указывают полином наименьшей степени g(x) , который полностью определяет код и называется порождающим. Степень порождающего полинома равна (n-k) , а свободный член V₀ всегда равен 1.

Порождающий полином используют для определения порождающей матрицы циклического кода:

1. В качестве первой строки матрицы записывают g(x), дополнив комбинацию нулями слева для получения кодового слова длиной n символов.

2. Вторая строка – x*g(x) (циклический сдвиг первой строки на одну позицию влево).

3. Третья строка – x²*g(x) (циклический сдвиг первой строки на две позиции влево).

……………………………………………………………………………………..

7. К-я строка – x^k-1*g(x) (циклический сдвиг первой строки на (k-1) позицию влево).

Пример.

З адан код (7,4) с порождающим полиномом g(x)=x³+x+1. Требуется записать его порождающую матрицу.

Полиномы кодовых слов циклического кода делятся без остатка на свой порождающий полином g(x).

Выбор g(x) для построения циклического кода длины n.

Любой полином, который является делителем полинома (xⁿ+1) можно использовать в качестве порождающего. С ростом n число возможных циклических кодов растет. На практике при построении циклических кодов пользуются таблицами разложения полиномов (xⁿ+1) на неприводимые полиномы. Любой неприводимый полином, входящий в разложение, или произведение нескольких неприводимых полиномов можно выбрать в качестве порождающего полинома, который дает соответствующий циклический код.

Пример.

Требуется определить, какие циклические коды можно построить при длине кодового слова n=7.

x⁷+1=(x+1)(x³+x²+1)(x³+x+1)

Можно построить следующие ЦК:

1. (7,6) с g(x)=x+1

2. (7,1) с g(x)= (x³+x²+1)(x³+x+1)=x⁶+x⁴+x³+x⁵+x³+x²+x³+x+1=

=x⁶+x⁵+x⁴+x³+x²+x+1

3. (7,4) c g(x)= x³+x²+1

4. (7,4) c g(x)= x³+x+1

5. (7,3) c g(x)= (x+1)(x³+x²+1)=x⁴+x³+x+x³+x²+1=x⁴+x²+x+1

6. (7,3) c g(x)= (x+1)(x³+x+1)=x⁴+x²+x+x³+x+1=x⁴+ x³+x²+1

Процедура кодирования циклическим кодом

Процедура кодирования записывается следующим образом:

V(x)=U(x)*x^n-k+R(x)

R(x)= U(x)*x^n-k mod g(x)

В этом случае первые k разрядов кодового слова являются информационными, а последние r=n-k - проверочными.

Пример

Закодировать информационную последовательность U=0110 циклическим кодом (7,4) с порождающим полиномом g(x)= x³+x+1.

U(x)= x²+x, r=n-k=3, U(x)*x³= x⁵+x⁴

R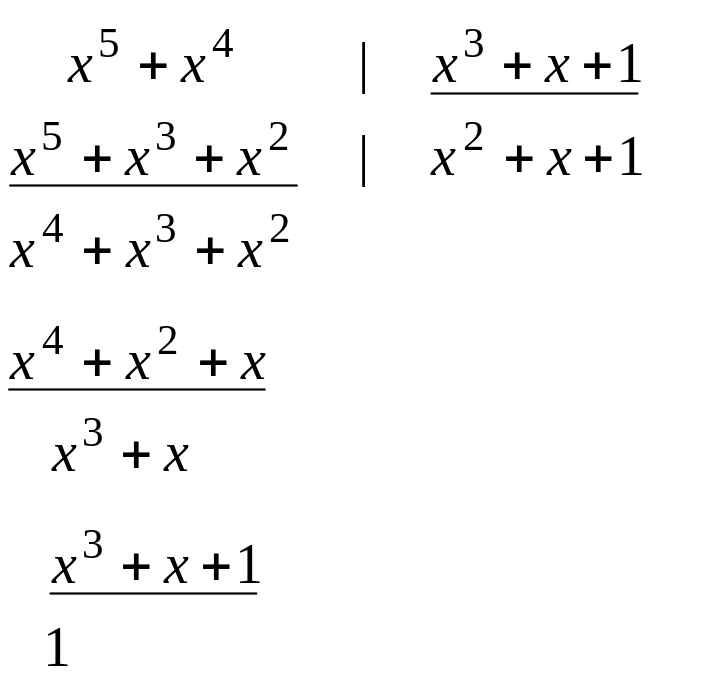 (x)=( x⁵+x⁴) mod (x³+x+1)

R(x)=1

V=0110001  V(x)= x⁵+x⁴+1

Сложение коэффициентов при одинаковых степенях осуществляется по модулю 2.

Деление можно выполнять в двоичном виде.

U(x)*x³= x⁵+x⁴  0110000

g(x)  1011

R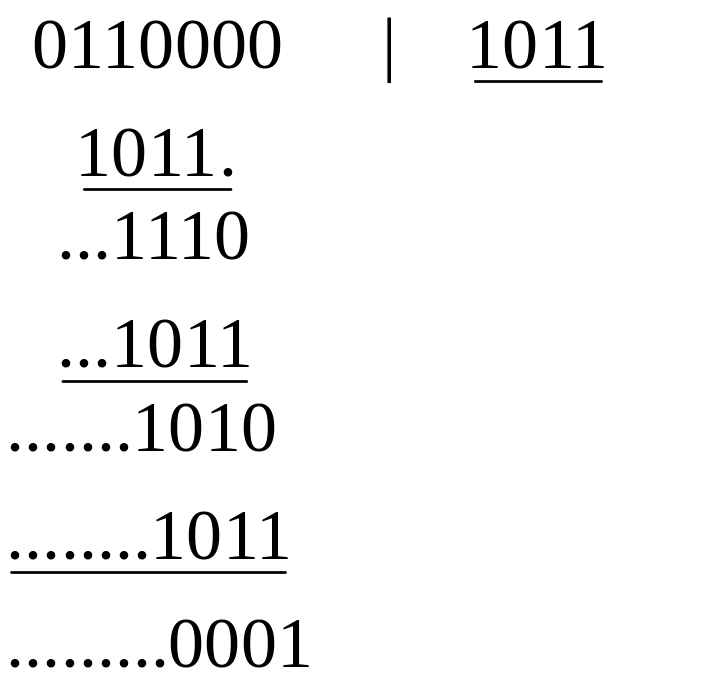 =001V=0110001

Число проверочных символов равно степени порождающего полинома.

Задача

Разделимый циклический код (7,4) задан порождающим полиномом

g(x)= x³+x²+1.

Соответствуют ли кодовые слова информационным последовательностям?

1. U₁=1101  V₁=1101000

2. U₂=0001  V₂=0001110

3. U₃=1011  V₃=1011100

Процедура декодирования циклического кода

В основу принципа декодирования циклического кода положено свойство делимости кодовых слов без остатка на порождающий полином.

Декодирование с обнаружением ошибок

Если принятая комбинация Y(x) делится без остатка на g(x), то считается, что ошибок нет или произошла не обнаруживаемая кодом ошибка. В случае обнаруженной ошибки имеет место ненулевой остаток от деления, который называется синдромом.

S(x)=Y(x) mod g(x)=e(x) mod g(x)

Здесь e(x) – полином ошибки.

Д еление на порождающий полином можно заменить умножением на проверочный полином h(x) по модулю (xⁿ+1). Результат в случае отсутствия ошибок должен быть равен нулю.

[Y(x)*h(x)] mod (xⁿ+1)=0

Декодирование с исправлением ошибок

Обычно в памяти декодера заданного циклического кода хранится некоторый типовой вектор ошибки и соответствующий ему типовой синдром.

Пусть ошибке вида e₀ соответствует синдром S₀. Назовем их типовыми.

S₀(x)=e₀(x) mod g(x)

Если вектор ошибки e' получается из e₀ путем i циклических сдвигов, то есть

e'(x)=e₀ (x)*xⁱ mod (xⁿ+1),

то синдром ошибки e' будет равен

S'(x)=S₀(x)*xⁱ mod g(x),

а S₀(x)= S'(x)* x^-i mod g(x)

Пример

Пусть для передачи сообщений используется циклический код (7,4) с порождающим полиномом g(x)= x³+x²+1. Декодер работает в режиме исправления одиночных ошибок.

При использовании ДСК без памяти таблица декодирования имеет вид

Вектор ошибки ei	Синдром Si
0000001	001
0000010 …………..	010 …….
1000000	110

В качестве типовых обычно выбирают e₀=0000001 и S₀=001.

Предположим при декодировании получен синдром S'=100. Требуется найти имеющий место вектор ошибки и исправить кодовое слово.

S₀(x)=S'(x)*x^-i mod g(x)

Если i=1, S₁= x²* x^-1 mod g(x)=x, не совпадает с типовым синдромом.

Если i=2, S₂=x²*x^-2 mod g(x)=1, совпадает с типовым синдромом.

Искомый вектор ошибки получается циклической перестановкой типового вектора e₀ на i=2 разряда влево.

e'=0000100

№8 Модеми

СИГНАЛЫ И ВИДЫ МОДУЛЯЦИИ, ИСПОЛЬЗУЕМЫЕ В УПС

Первые лекции данной дисциплины рассматривали преобразование сообщений в системах ПДС. С точки зрения используемых технических средств в системах ПДС выделяют три класса устройств:

• Оконечные устройства и устройства сопряжения. В частности преобразования, относящиеся к кодированию источника, выполняются в оконечных устройствах.

• Устройства защиты от ошибок (УЗО). Они выполняют кодирование для канала и обычно представляют собой систему с обратной связью. Различные алгоритмы работы систем с обратной связью изучаются в рамках курсовой работы по ПДС.

• Устройства преобразования сигналов (УПС). Предназначены для формирования и приема сигналов, непосредственно передающихся по непрерывному каналу связи. В современной технической литературе УПС чаще называют модемами.

В системах передачи данных оконечная установка передачи данных включает в себя оконечное оборудование данных (ООД) и аппаратуру передачи данных, которая в соответствии с рекомендациями Международного Союза Электросвязи (МСЭ-Т, ранее МККТТ) называется аппаратурой окончания канала данных АКД (аппаратура канала данных). АКД (или модем) обычно выполняет функции УЗО и УПС.

Сигналы, используемые в УПС, и методы передачи определяются средой передачи, то есть видом непрерывного канала связи. Рассмотрим три типовые среды в системах проводных телекоммуникаций:

1. Арендованная физическая линия, обычно представляет собой пару симметричного кабеля.

2. Стандартный канал тональной частоты с полосой пропускания 300 – 3400 Гц.

3. Синхронный цифровой поток, доведенный до потребителя по абонентской линии.