Тема. Основні поняття, аксіоми планіметрії і стереометрії та наслідки з них

План

1. Аксіоми стереометрії.

2. Існування площини, що проходить через дану пряму і дану точку

3. Перетин прямої площиною

4. Існування площини, що проходить через три дані точки

5. Розбиття простору площиною на два півпростори

1. Аксіоми стереометрії

Стереометрія — це розділ геометрії, у якому вивчаються фігури у просторі. У стереометрії, як і в планіметрії, властивості геометричних фігур встановлюються доведенням відповідних теорем. При цьому вихідними є властивості основних геометричних фігур, які виражаються аксіомами. Основними фігурами у просторі є точка, пряма і площина.

Площину ми представляємо як гладку поверхню стола (мал. 1, а) і будемо зображувати її у вигляді паралелограма (мал. 1, б). Площина, як і пряма, нескінченна. На малюнку ми зображуємо тільки частину площини, але уявляємо її необмежено продовженою в усі боки. Площини позначаються грецькими буквами α, β, γ, … .

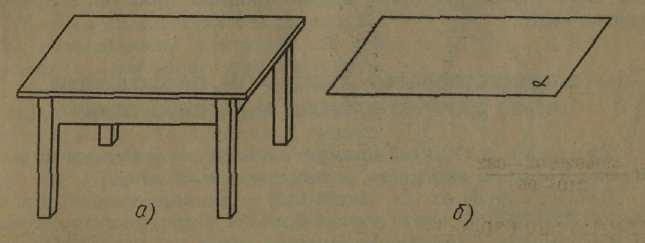
Мал. 1

Введення нового геометричного образу — площини - вимагає розширення системи аксіом. Тому ми вводимо групу аксіом С, що виражає основні властивості площин у просторі. Ця група складається з таких трьох аксіом:

С₁. Яка б не була площина, існують точки, які належать цій площині, і точки, які їй не належать.

С₂. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.

Ця аксіома стверджує, що якщо дві різні площини α і β мають спільну точку, то існує пряма с, яка належить кожній із цих площин. При цьому, якщо точка С належить обом площинам, то вона належить прямій с.

С₃. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.

Це значить, що якщо дві різні прямі а й b мають спільну точку С, то існує площина γ, яка містить прямі а і b. Площина, що має цю властивість, єдина.

Таким чином, система аксіом стереометрії складається з аксіом I-IX планіметрії і групи аксіом С.

Зауваження. У планіметрії ми мали одну площину, на якій розміщалися всі розглянуті фігури. У стереометрії багато, навіть нескінченно багато, площин. У зв'язку із цим формулювання деяких аксіом планіметрії, як аксіом стереометрії, вимагають уточнення. Це стосується, наприклад, аксіом IV, VII, VIII, IX. Наведемо ці уточнені формулювання.

IV. Пряма, що належить площині, розбиває цю площину на дві півплощини.

VII. Від напівпрямої на площині, яка містить її, можна відкласти в задану півплощину кут з даною градусною мірою, меншою 180⁰, і тільки один.

VIII. Яким би не був трикутник, існує трикутник, що дорівнює йому, у даній площині у заданому розміщенні відносно даної напівпрямої у цій площині.

IX. На площині через дану точку, яка не лежить на даній прямій, можна провести не більш яу одну пряму, паралельну даної.

Для зручності викладу нагадаємо аксіому I.

I. Яка б не була пряма, існують точки, які належать цій прямій, і точки, які не належать їй. Через будь-які дві точки можна провести пряму, і тільки одну.

2. Існування площини, що проходить через дану пряму й дану точку

Теорема 1.1. Через пряму і точку, що не лежить на ній, можна провести площину, і до того ж тільки одну.

Доведення. Нехай АВ— дана пряма й С — точка, яка не лежить на ній (рис. 2). Проведемо через точки А и С пряму (аксіома I). Прямі АВ і АС різні, тому що точка С не лежить на прямій АВ.

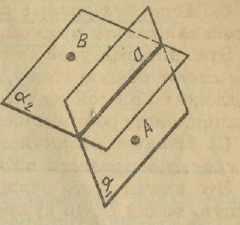
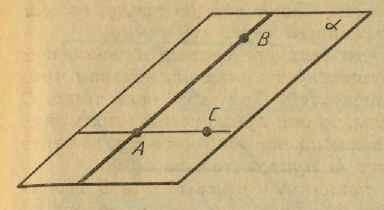
Мал. 2 Мал.3

Проведемо через прямі АВ і АС площину α (аксіома С₃). Вона проходить через пряму АВ і точку С.

Доведемо, що площина α, яка проходить через пряму АВ і точку С, єдина.

Допустимо, існує інша площина α', що проходить через пряму АВ і точку С. По аксіомі С₂ площини α і α' перетинаються по прямій. Ця пряма має містити точки А, В, С. Але вони не лежать на одній прямій. Ми прийшли до суперечності. Теорему доведено.