Тема.
Основні
закони та правила алгебри.
Дії зі звичайними та десятковими дробами.
Формули
скороченого множення. Спрощення
раціональних виразів.
План
Числові множини.
Основні закони та правила алгебри.
Дії зі звичайними та десятковими дробами.
Формули скороченого множення.
Спрощення раціональних виразів.
1. Числові множини |
||||||
Дійсні числа R |
||||||
Числа, які можна подати у вигляді нескінченного десяткового дробу |
||||||
|
||||||
Раціональні числа Q |
Ірраціональні числа |
|||||
Можна подати у вигляді
нескоротного дробу
Записують у вигляді нескінченного періодичного десяткового дробу
|
Не можна подати у вигляді нескоротного дробу , де m – ціле, n – натуральне число. Записують у вигляді нескінченного неперіодичного десяткового дробу
|
|||||
|
||||||
Цілі числа Z |
Дробові числа |
|||||
В |
Числа , складені із цілого
числа часток одиниці
1,23
– десятковий дріб: 1,23 =
|
|||||
|
||||||
Натуральні числа N (цілі додатні) |
Число 0 |
Цілі від’ємні числа |
||||
У шкільному курсі математики натуральне число – основне неозначуване поняття |
Таке число, що будь-яке число при додаванні до нього не змінюється а + 0 = 0 + а = а |
Числа, протилежні натуральним |
||||
|
||||||
2. Основні закони та правила алгебри |
||||||
Основні арифметичні дії |
Властивості |
|||||
Переставна |
Сполучна |
Розподільна |
||||
Додавання: a + b = c |
a + b = b + a |
a + (b + c) = (a + b) + c |
- |
|||
Віднімання: a - b = c |
a - b = - (b – a) |
a - (b - c) = a - b + c (a – b) - c = a - b - c |
- |
|||
Множення: a
|
a b = b a |
(a b) c = a (b c) |
(a + b) c = ac + bc (a - b) c = ac - bc |
|||
Ділення: a : b = c |
|
Ділення числа на добуток: c : (ab) =(c : a):b = (c : b): a; ділення добутку на число: (ab) : c =(a : c) b = (b : c) a |
Ділення суми (різниці) на
число:
|
|||
,
де m
– ціле, n
– натуральне число.
ключають
натуральні числа, числа, їм протилежні,
та число 0
- звичайний дріб,
b = c
Властивості 0 та 1 |
|
a + 0 = a; a – 0 = a; 0 – a = - a; a + (- a) = 0; a – a = 0 (a та – а протилежні числа).
а (а
та |
аb = 0, якщо а = 0, або b = 0, або а = b = 0
|
Вважають, що 0 ділиться на будь-яке число, але ділити на нуль не можна! |
|
|
|
3. Дії зі звичайними та десятковими дробами |
|
Правила |
Приклади |
Основна властивість дробу |
|
Значення дробу не зміниться, якщо чисельник і знаменник дробу помножити або поділити на одне і те саме число (вираз), яке не дорівнює нулю. |
=
|
Скоротити дріб – означає поділити чисельник і знаменник дробу на спільний дільник. |
=
; |
Порівняння дробів |
|
З двох дробів з однаковими знаменниками більший той дріб, чисельник якого більший |
|
Якщо знаменники різні, то треба дроби звести до спільного знаменника і порівняти їх як дроби з рівними знаменниками. |
|
З двох дробів з рівними чисельниками той дріб більший, у якого знаменник менший. |
|
Додавання і віднімання |
|
Якщо знаменники рівні, то чисельники додаються (віднімаються), а знаменник зберігається. |
|
Якщо знаменники різні, то спочатку дроби зводять до спільного знаменника і додають (віднімають) їх як дроби з рівними знаменниками. |
|
При додаванні (відніманні) мішаних чисел можна додати (відняти) їх цілі і дробові частини. |
|
Множення дробів |
|
При множенні дробів помножують чисельники і знаменники |
|
При множенні мішаних чисел їх спочатку перетворюють у неправильні дроби, а потім помножують їх. |
2 |
Якщо в добутку один з множників – ціле число, то його подають у вигляді дробу із знаменником 1.
|
|
Ділення дробів |
|
При
діленні двох дробів ділення замінюють
множенням першого дробу на обернений
другий дріб.
:
=
|
|
4. Формули скороченого множення |
|
Квадрат суми |
|
Квадрат різниці |
|
Різниця квадратів |
|
Куб суми |
|
Куб різниці |
|
Сума кубів |
|
Різниця кубів |
|
|
|
Пропорції |
|
Пропорція
– це рівність двох відношень.
=
або а :
b = c
: d (a,b,c,d
Члени пропорції: a, d – крайні члени, b,с – середні члени. |
|
Основна властивість пропорції: добуток крайніх членів пропорції дорівнює добутку її середніх членів. ad = bс |
|
- обернені)
= 0 тільки при а
= 0, b
0
,
,
оскільки 2 <
11
і
;
=
;
=
;
<
,
тобто
<
.
<
,
оскільки 15
<
17.
=
=
=
=
).
Тема. Повторення. Дії зі звичайними та десятковими дробами.
Розв’язати:
(-1,73 – 2,77) ∙ 0,4;
999 ∙ 1001+1001;
- 0.6 ∙ (-0.3) – 0.2;
(3.1 + 0.09)0;
(-7 + 2.5) : 1.5;
0.62 : 0.4 – 1;
(-2.35 – 5.15) : 15;
(-1.32 – 2.18) ∙ 0.6;
(-6 + 1.2) : (-0.8);
(0.1 – 0.8)2;
(0.3 – 0.5)2;
(0,7 – 3,2) : (-0.5);
– 2.4 : 0.8 + 1.6;
(0,3 – 0,5)0 : 0.2;
(-1.4 + 0.8) : 0.2;
(-5 + 1,4): (-1.2);
(-6 + 1,8) : (-0.6);
−2.8 : 0.7 + 2.4;
(-1.8 + 0.4) : 0.01;
(0.4 - 1)2;
0.42 : 0.2 – 1;
(- 2.16 – 4.24) : (-16);
(1.2 – 2.9) (-1.7);
– 0.7 ∙ (-0.4) – 0.3;
(0.4 – 0.7)2;
(2.3 + 0.07)0 ;
(0.3 – 3.9) : 0.6;
(-2.6 + 0.5) : (-0.01);
(-0.1)2 + 2.34;
(-0.6 + 2.6)4;
(-1.2 + 0.4) : 0.4;
(-0.8 + 3.8)3;
3.76 + (-0.1)2.
2. Обчислити:
1)
+
(
4)
: 1
;
2) 2
:
13 + (3
+
2
)
: 2
;
3) 2
:
4 + (14
)
: 1
+
3
;
4) 23 + (7
- 6
)
:
-
5
;
5) 32 + (4
- 3
)
: 1
+
3
;
6) 4
+
·
(7
:
);
7) 6
:
1
+
:
;
8) 5
-
·
(5
:
1
);
9) (15 :
)
: (3
·
);
10)
·
(1
:
)
·
;
11)
·
(1
:
)
: 2;
12)
·
5
:
(
:8).
3.Обчислити раціональним способом:
(1
+ 0,25 - 3
-
1
):
2
(1 - 0,75 - 4
-
)
: 1
(1,82 – 2,3) · 1
:
2
(1,52 - 2
·
1
)
: 1
4.Обчислити:
1)
;
2)
;
3) (4,3 ∙
+
11
·
2,25) : 2,75
(0,3 -
)
∙
1,5 (1,88 + 2
);
;
Тема. Повторення. Формули скороченого множення
Розкласти на множники
25х2 – 9
4a2 – 9
64y2 – 36x2
0,25a2 – 0,49b2
0,09a2 - 0,16b2
36x2y2 – 1
x2y2 – 16
81y2 – 49y2
25a2 – 9b2
b2 – 81
(с + d)2
(x - y)2
(2 + x)2
(y +1)2
(g + 2p)2
(3x + 2y)2
(6a – 4b)2
(5z - t)2
(0,2x + 0,3y)2
(0,4b - 0,5c)2
Виконати множення
(2b - a) (2b + a)
(c2 – d2) (c2 + d2)
(x4 + y2) (x4 – y2)
(3m + 2n) (3m – 2n)
(a2 – b3) (a2 + b3)
(3a2 – 4b3) (3a2 + 4b3)
(0,2t2 – 0,5p4) (0,2t2 + 0,5p4)
(2m4 – 5n2) (2m4+ 5n2)
Розкласти на множники
(a + b)2 – c2
(a + 2b)2 – 9a2
(m - n)2 – k2
(3x - y)2 – 4y2
(a - b)2 – (a - c)2
(a + b)2 – (b + c)2
(2a +b)2 – (2b + a)2
(a +3b)2 – (3a + b)2
a2 + 4a + 2
9a2 – 6a + 1
1 + 2c + c2
36b2 + 12b + 1
81 – 18x + x2
9x2 + 24x + 16
36m2 + 12mn + n2
x4 + 2x2 y + y2
100 – 60a + 9a2
p4 – 2p2g + g2
27a3 – b3
8m3+ n3
x3y3 + 64
c6 – 125d3
Обчислити
472 - 372
542 - 442
50,72 – 50,62
29,42 – 29,32
(90 - 1)2
(40 + 1)2
1012
982
722
572
Тема. Рівняння та нерівності, їх розв'язування. Лінійні та квадратні рівняння, нерівності. Рівняння, що зводяться до квадратних
План
Рівняння, їх розв'язування.
Нерівності, їх розв'язування.
Лінійні рівняння.
Лінійні нерівності.
Квадратні рівняння.
Рівняння, що зводяться до квадратних.
Квадратні нерівності.
1. Рівняння, їх розв'язування |
||
Означення |
Приклади |
|
Рівняння – це рівність, яка містить змінну.
Розв’язок рівняння – це значення змінної, при якому рівняння перетворюється у правильну рівність. |
3(х – 4) = 24, (х – 4) = 24 : 3, х – 4 = 8, х = 8 + 4, х =12 – розв’язок рівняння |
|
Розв’язати рівняння – це означає знайти його розв’язки або довести, що їх немає. |
3(х – 4) = 24, х =12
|
|
Рівносильні рівняння – це рівняння, які мають одні і ті самі розв’язки. |
3х = 36 і 3(х – 4) = 24; їх розв’язок х =12 |
|
Деякі властивості рівнянь |
||
У будь-якій частині рівняння можна звести подібні доданки. Якщо з однієї частини рівняння перенести доданки в іншу частину і при цьому змінити знаки доданків на протилежні, отримаємо рівняння, рівносильне даному. |
3х – 4 +5х = 36 3х + 5х = 36 + 4 8х = 40
|
|
При діленні (множенні) обох частин рівняння на одне і те саме число, відмінне від нуля, отримаємо рівняння, рівносильне даному. |
Поділимо обидві частини рівняння 8х = 40 на 8: х = 5 – це рівняння рівносильне 8х = 40, їх розв’язок 5. |
|
2. Нерівності, їх розв'язування |
||
Якщо а менше b або а більше b, то записують так: а < b або а > b. Такий вираз називається нерівністю. |
7 < 10; 8 > 7 |
|
Знаки < , > називаються знаками строгих нерівностей. |
а < b ; а > b |
|
Знаки
|
а b; а b |
|
3. Лінійні рівняння |
||
Рівняння виду ax = b, де х - змінна, а і b- деякі числа, називається лінійним рівнянням. |
4- 5х = 6 – 2(х + 2), -3х = -2 х
=
|
|
Розв’язування лінійних рівнянь |
||
ax + b = 0; ax = - b |
5х + 4 = 0, 5х = -4 |
|
a
0;
х = - |
х
= - |
|
а = 0, 0х = - b – немає розв’язків |
0х = -10 немає розв’язків – 10 на 0 поділити неможливо |
|
а = 0, b = 0. 0 х = 0 – нескінчена множина розв’язків |
7х = 7х, 7х - 7х = 0, 0х = 0 х – будь-яке число |
|
Розв’язування лінійних рівнянь з двома змінними |
||
Лінійним рівнянням з двома змінними х и у називається рівняння виду: ах + bу + с = 0, де х и у - змінні, а, b, с – деякі числа. |
3х + 4у + 5 = 0 – лінійне рівняння |
|
Розв’язком рівняння з двома змінними називається будь-яка пара чисел (х; у), яка перетворює рівняння на тотожність. Розв’язати рівняння з двома змінними – означає знайти всі пари чисел (х; у), які є його розв’язком. |
х + 2у = 5 – лінійне рівняння Пара (1; 2) – розв’язок рівняння
|
|
4. Лінійні нерівності |
||
Лінійною називається нерівність виду ах > b (або,
відповідно,
ах
< b,
ах
b,
ах
b
), де
|
||
Розв’язками нерівності з однією змінною називається множина таких значень змінної, яка перетворює її на правильну числову нерівність. |
||
Властивості |
Приклади |
|
Якщо з однієї частини нерівності перенести в іншу доданок з протилежним знаком, то утвориться нерівність, рівносильна даній |
4(у - 1) + 7 1 – 3(у + 2), 4у – 4 + 7 1 – 3у – 6, 4у + 3у 1 – 6 – 7. |
|
Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то утвориться нерівність, рівносильна даній |
7у -8, у
-
|
|
Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то отримуємо рівносильну даній нерівність. |
- 3х + 8 < 2х – 2, - 5х < -10, х > 2
|
|
5. Квадратні рівняння |
||
Рівняння виду ах2 + bх + с = 0, де х - змінна, а, b, с – деякі числа, причому а 0, називають квадратним рівнянням. а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член |
|
|
Якщо в цьому рівнянні хоча б один з коефіцієнтів дорівнює нулю, то дане рівняння називають неповним квадратним рівнянням. Неповні квадратні рівняння бувають трьох видів: 1) ах2 = 0; 2) ах2 + bх = 0; 3) ах2 + с = 0 |
||
ах2 = 0 при b = 0, с = 0 х2 = 0 х = 0 рівняння має тільки один розв’язок |
5х2 = 0 х2 = 0 х = 0 |
|
ах2 + bх = 0 при с = 0 х(ах + b) = 0 х1
= 0 або х2
=
рівняння завжди має два розв’язки |
4х2 + 3х = 0 х(4х + 3) = 0 х1
= 0 або х2
=
|
|
ах2 + с = 0 при b = 0 ах2 = - с х2
= -
оскільки с 0, то - 0, тоді: 1) якщо - > 0, то рівняння має два розв’язки х1
= - 2) якщо - < 0, то рівняння не має розв’язків |
9х2 - 4 = 0 9х2 = 4 х2
=
х1 = - ; х2 = ;
16х2 + 9 = 0 16х2 = - 9 х2
= -
немає розв’язків |
|
Якщо а =1, то квадратне рівняння називають зведеним |
х2 -bх + 30 = 0 |
|
Повні
квадратні рівняння
ах2
+ bх
+ с = 0 розв’язуємо
за формулою
х1,2
=
де
D =
|
||
Якщо D < 0, то рівняння не має дійсних розв’язків |
2х2 + 5х + 6 = 0 D = 25 – 48 = - 23 D < 0, отже, рівняння не має дійсних розв’язків |
|
Якщо D = 0, то рівняння має два однакові розв’язки: х1
=
х2
=
|
4х2 + 4х + 1 = 0 D = 16 – 16 = 0 D = 0, отже, рівняння має два однакові розв’язки: х1
=
х2
=
|
|
Якщо D > 0, то рівняння має два різні розв’язки: х1
=
|
2х2 + 3х + 1 = 0 D = 9 – 8 = 1, D > 0, отже, рівняння має два різні розв’язки: х1
=
|
|
Теорема Вієта |
||
ах2
+ bх
+ с = 0,
Якщо
а
= 1, то
|
|
|
6. Рівняння, що зводяться до квадратних |
||
Рівняння виду ах4 + bх2 + с = 0, де а 0, b 0 називається біквадратним рівнянням |
2х4 + 3х2 + 4 = 0 |
|
Формула
розкладу квадратного тричлена на
множники: ах2
+ bх
+ с =а( |
2х2 - х - 3 =2( )( ); 2х2 - х - 3 =0, х1 = 1,5; х2 = - 1 2х2
- х - 3 =2(
|
|
7. Квадратні нерівності |
||
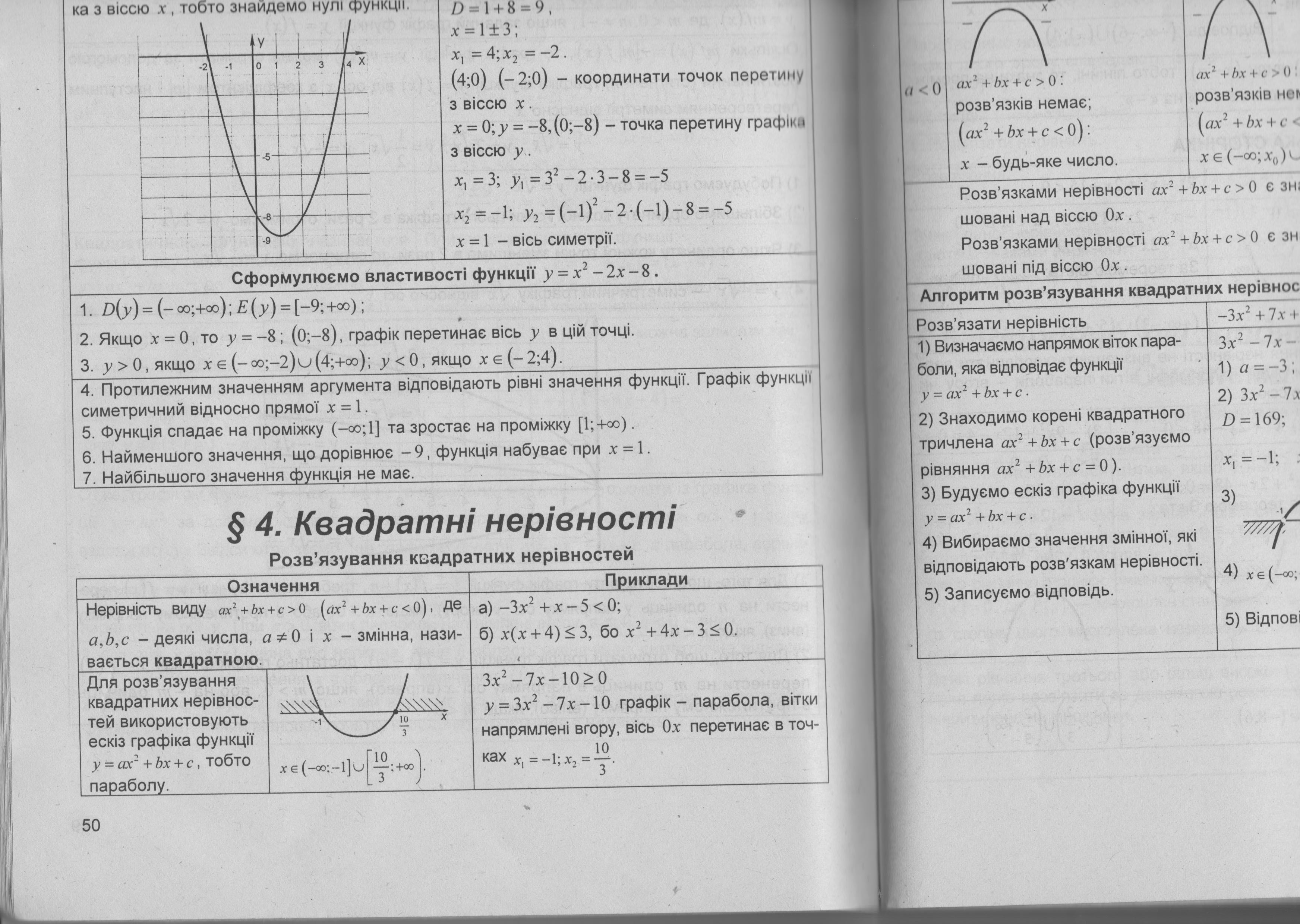
Нерівність виду ах2 + bх + с < 0(ах2 + bх + с>0), де х - змінна, а, b, с – деякі числа, причому а 0, називають квадратною. |
3х2 + 4х - 5 < 0 - 5х2 - 6х+7 > 0 |
|
Для розв’язування квадратичних нерівностей використовують ескіз графіка функції у = ах2 + bх + с, тобто параболу |
х |
3х2 - 7х - 10 0 у = 3х2 - 7х – 10 – графік - парабола, вітки напрямлені вгору, вісь Ох перетинає в точках |
,
називаються знаками нестрогих
нерівностей.
- єдиний
розв’язок
- розв’язок
- числа.
;
х2
=
;
,
називають дискримінантом даного
квадратного рівняння
,
х2
=
,
,
х2
=
.
,
,
)(
)
)(
).
Тема. Рівняння
Розв’язати рівняння
25х – 1 = 9
7х + 8 = 11
3х – 5 = 10 – х
4х + 4 = х + 5
5х + 3(3х + 7) = 35
8у – 9 – (4у - 5) = 12у - (4 + 5у)
8х – (7х + 8) = 9
4 + 8у + 8 = 2у – (10 + 7у) + 9
Розв’язати рівняння
5(х - 3) – 2(х - 7) + 7(2х + 6) = 7
11(у - 4) + 10(5 – 3у) -3(4 – 3у) = - 6
5(8х - 1) – 7(4х + 1) + 8(7 – 4х) = 9
10(3х - 2) – 3(5х + 2) + 5(11 – 4х) = 25
0,71х + 1,98 = 0,37х – 1,76
0,18у – 7,4 = 0,05у – 5,71
5(5х - 1) – 2,7х + 0,2х = 6,5 – 0,5х
0,36х – 0,6 = 0,3(0,4 – 1,2)
Розв’язати рівняння
2 -
Розв’язати рівняння
Розв’язати рівняння
4х2 – 9 = 0
-х2 + 3 = 0
6у2 +24 = 0
3х2 - 1 = 0
Розв’язати рівняння
3х2 – 4х = 0
-5х2 + 6х = 0
10х2 + 7х = 0
2у + у2 = 0
Розв’язати рівняння
3х2 - 7х + 4 = 0
5х2 - 8х + 3 = 0
3х2 - 13х + 14 = 0
2у2 – 9у + 10 = 0
5у2 – 6у + 1 = 0
4х2 + х - 33 = 0
Розв’язати рівняння
Тема. Нерівності
Розв’язати нерівність
Розв’язати нерівність
Розв’язати нерівність
Розв’язати систему лінійних нерівностей
Розв’язати квадратну нерівність
Розв’язати нерівність
Тема. Корінь n-го степеня і його властивості. Арифметичний корінь n-го степеня, його властивості. Перетворення коренів. Степінь з раціональним показником, дії над степенями
План.
Корінь n-го степеня і його властивості.
Арифметичний корінь n-го степеня, його властивості.
Перетворення коренів.
Степінь з раціональним показником, дії над степенями.
Розв’язання вправ.
1-3. Квадратний корінь із числа а це таке число, квадрат якого дорівнює а. Аналогічно визначається корінь n-го степеня з числа а, де п — довільне натуральне число.
Коренем n-го степеня з числа а називається таке число, n-й степінь якого дорівнює а.
Приклад 1. Корінь третього степеня з числа 27 рівний 3, тому що 33 = 27. Числа 2 і -2 є коренями шостого степеня з числа 64, оскільки 26 = 64 і (- 2)6 = 64.
Як і для квадратного кореня, для кореня n-го степеня вводять поняття арифметичного кореня.
Арифметичним коренем п-го степеня з числа а називається невід’ємне число, п-й степінь якого дорівнює а.
При
для
арифметичного значення кореня п
-го степеня з числа а існує спеціальне
позначення:
;
число
п
називають
показником
кореня, а
саме число а
—
підкореневим
виразом.
Знак
кореня
і вираз
називають
також радикалом.
Приклад 2. Знайти значення:
а)
;
б)
.
а)
= 2, тому що 2
= 8 і 2 > 0;
б)
=
,
тому що
=
і
>
0.
При
a
> 0
значення кореня п-го
степеня з числа
а
існує тільки при непарних значеннях
п
(оскільки не існує такого дійсного
числа, парний степінь якого буде
від’ємним числом). У цьому випадку
корінь непарного степеня з числа
а
теж позначають
.
Наприклад, те, що корінь третього степеня
з числа -27 дорівнює -3, записують так:
.
Оскільки -3 – від’ємне число, то
не
є арифметичним значенням кореня. Але
корінь непарного степеня з від’ємного
числа можна виразити через арифметичне
значення кореня за допомогою формули
= -
.
Наприклад,
=
-
,
=
-
.
Зауваження
1.
Зручно вважати, що корінь першого
степеня із
числа а
рівний
а.
Як
ви вже знаєте, корінь другого степеня
з
числа називають квадратним
коренем, а
показник 2 кореня при
записі опускають (наприклад, корінь
квадратний з 7 позначають
просто
).
Корінь третього ступеня називають
кубічним
коренем.
Приклад 3. Розв'яжемо рівняння: а) х5= -11; б) х8 = 7.
а) З
визначення кореня n-го
степеня
число
х
-
корінь п'ятого
степеня з -11.
Показник кореня - непарне число 5, тому
такий корінь існує й притому тільки
один: це
.
Отже, х
= -
.
б) З
визначення кореня n-го
степеня
розв’язанням
рівняння х8
= 7 є число
.
Тому
що 8 — число парне, -
також є
рішенням даного рівняння. Отже, х1
=
,
х2
= -
.
Відповідь можна записати так: х= ± .