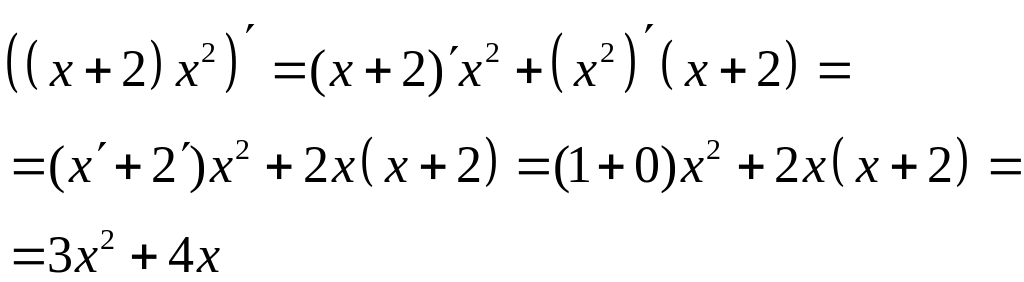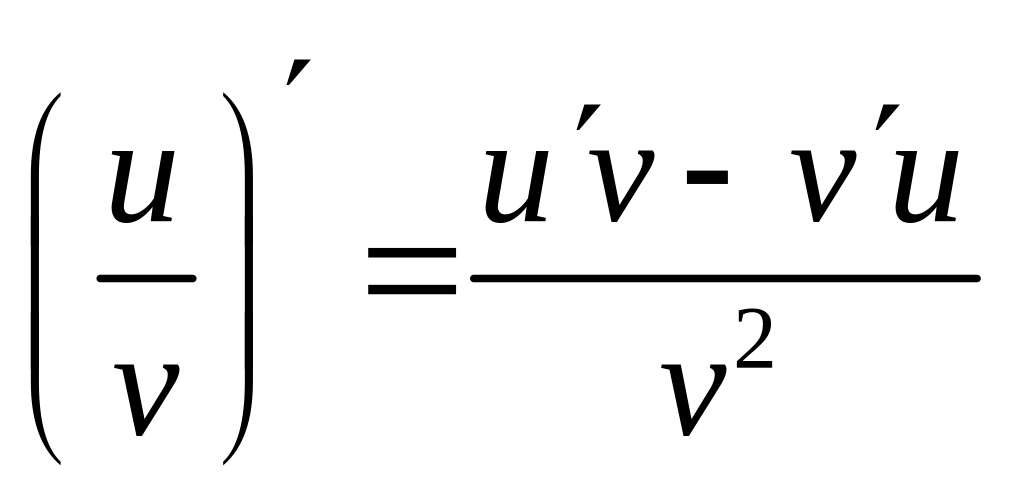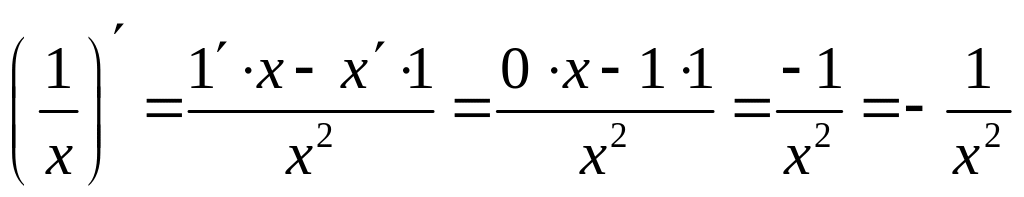- •Тема. Границя функції в точці та на проміжку. Властивості границь. Неперервність функції в точці та на проміжку. Властивості неперервних функцій
- •Властивості границь
- •Функція f(X) називається неперервною в точці а, якщо при , тобто
- •Тема. Приріст аргументу і приріст функцій. Задачі, які приводять до поняття похідної. Означення похідної, механічний та геометричний зміст
- •Механічний зміст похідної
- •Тема. Похідні елементарних функцій . Правила диференціювання функцій
- •Тема. Похідна складної функції
- •Формула похідної складної функції.
- •Тема. Похідна показникової та логарифмічної функцій
- •Тема. Дотична до графіка функції. Рівняння дотичної до графіка функції.
- •Тема. Монотонність функції, ознаки сталості, зростання і спадання функції
- •Тема. Екстремуми функції (максимальні та мінімальні значення функції). Дослідження функції на екстремуми
- •Тема. Опуклість та гнучкість функції. Дослідження функції на опуклість та точку перетину
- •Тема. Застосування похідної до побудови графіків функцій
- •Тема. Найбільше і найменше значення функції
Механічний зміст похідної
Похідна характеризує швидкість зміни функції при зміні аргументу |
|
S = S (t) – залежність пройденого шляху від часу
V = S ′(t) – швидкість прямолінійного руху
a = v′(t) – прискорення прямолінійного руху |
Зокрема, похідна за часом є мірою швидкості зміни відповідної функції, що може застосовуватися до найрізноманітніших фізичних величин. Наприклад, миттєва швидкість v нерівномірного прямолінійного руху є похідна функції, яка виражає залежність пройденого шляху s від часу t. |
Зв'язок між диференційованістю і неперервністю функції
Якщо функція f(х) диференційована в точці х0, то вона неперервна в цій точці.
|
Якщо функція f(х) диференційована на проміжку (тобто в кожній його точці), то вона неперервна на цьому проміжку |
Тема. Похідні елементарних функцій . Правила диференціювання функцій
План
Похідні елементарних функцій.
Правила диференціювання функцій.
1. Похідні елементарних функцій |
|||
1 |
|
8 |
|
2 |
|
9 |
|
3 |
|
10 |
|
4 |
|
11 |
|
5 |
|
12 |
|
6 |
|
13 |
a - стала |
7 |
|
14 |
на ОДЗ правої частини формули |
|
|||
2. Правила диференціювання функцій |
|||
Правило |
Приклад |
||
Сталий множник можна виносити за знак похідної |
|
||
Похідна суми диференційованих функцій дорівнює сумі їх похідних |
|
||
|
|
||
|
|
||
Вправи
Для функції у = 2х знайдіть приріст функції ∆у, який відповідає приросту аргументу ∆х у точці х0, якщо:
1) х0 = 2 і ∆х = 3; 2) х0 = 1,5 і ∆х = 3,5; 3) х0 = 0,5 і ∆х = 2,5.
Знайдіть приріст ∆у, який відповідає приросту аргументу ∆х у точці х0 для функції:
1) у = 3х; 2) у = х3; 3) у = х2 – х.
Користуючись схемою обчислення похідної, знайдіть похідну функції:
1) у = 3х; 2) у = -5х; 3) у = х3.
Знайдіть похідну функції:
у = х8;
у = х -5;
у = х
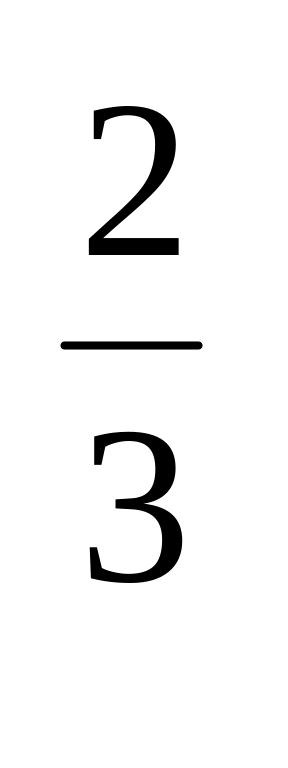 ;
;у = х20;
у = х -20;
у = х
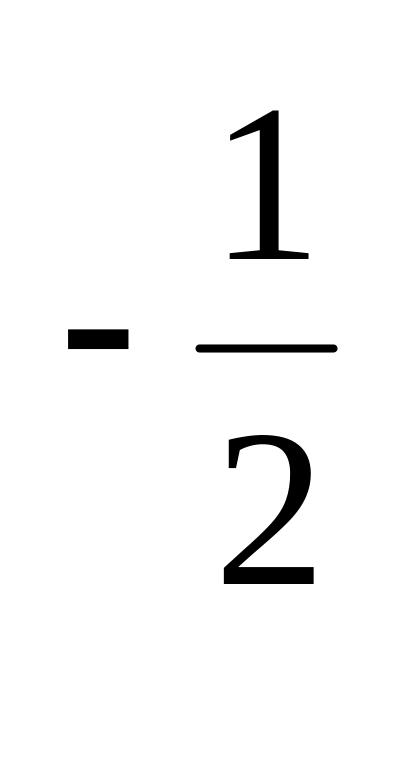 ;
;у = х + 3;
у = х5 - х;
у =
 - х3;
- х3;у = х2 +
 ;
;у = 2х3 + 3х;
f(x) = х2 +5x + 2;
f(x) = х4 - 2x2 - 1;
f(x) = 2 + 4х3 + 3;
f(x) = х5 +
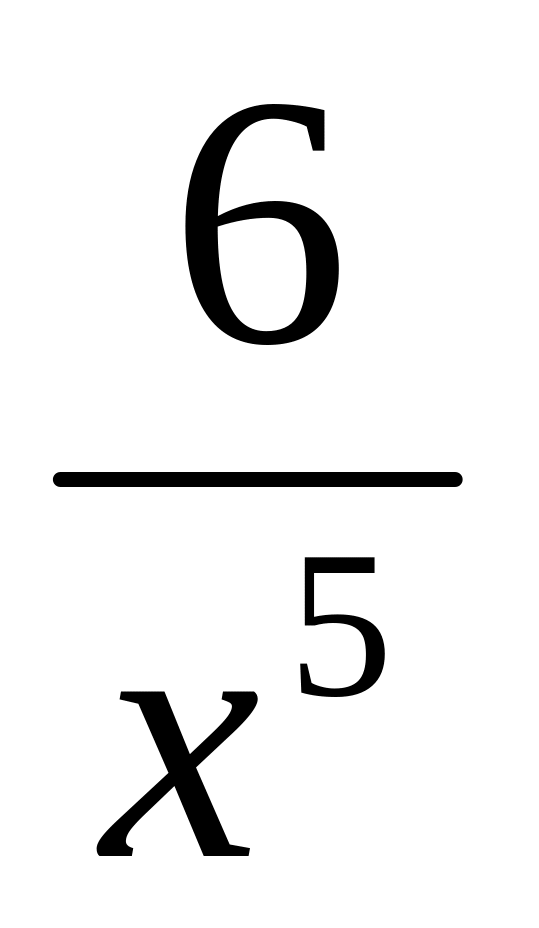 ;
;f(x) = х2 +
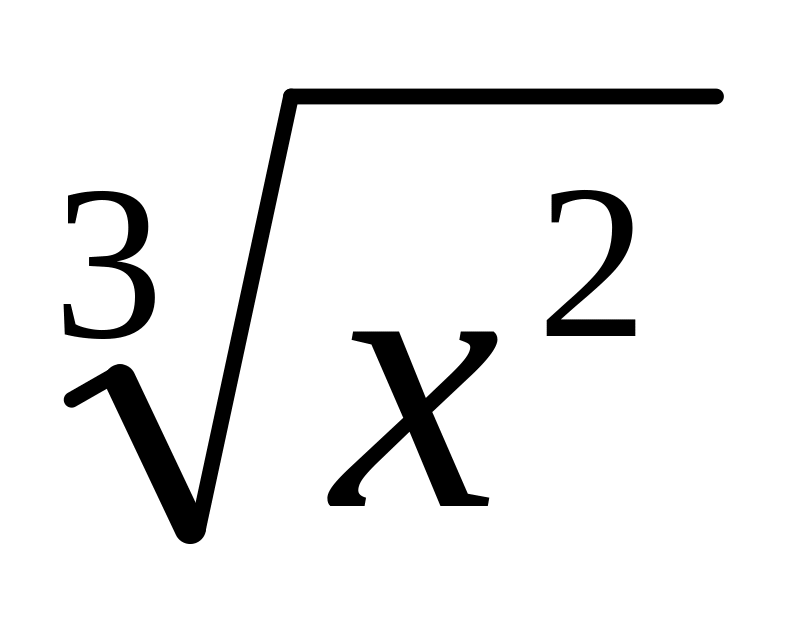 ;
;f(x) =
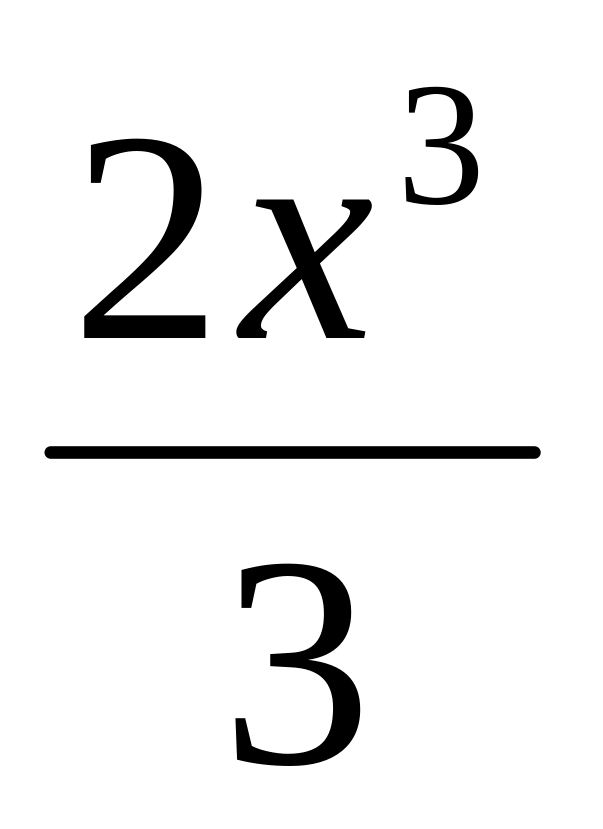 - 3х2
+ 6х – 1.
- 3х2
+ 6х – 1.
Знайдіть похідну функції:
у = x2(х + 2);
у = x2(2х + х4);
у = (2х - 1)(1 - x2);
у = (3 + х3)(2 - x);
у = (х9 + 11)(х2 - 4);
у = (х8 - 2);
у = (3х2 - х);
у = (х2 - 1)(x5 + 2);
у = (2х + 9);
у = (х3 + 16) ;
у =
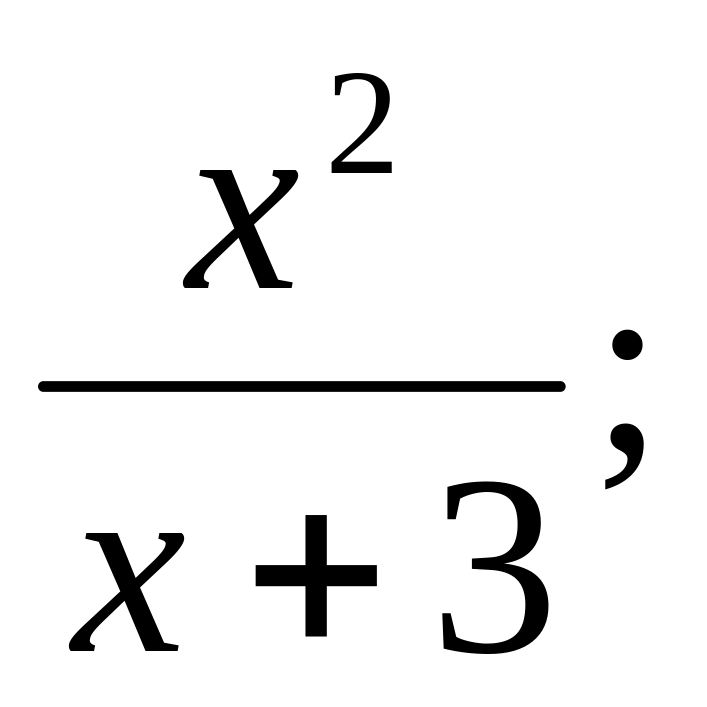
у =
у =
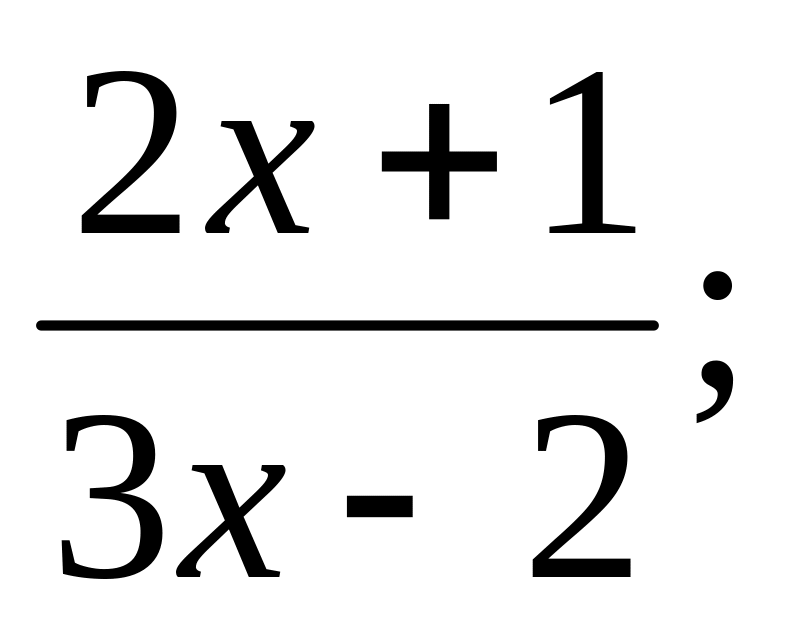
у =
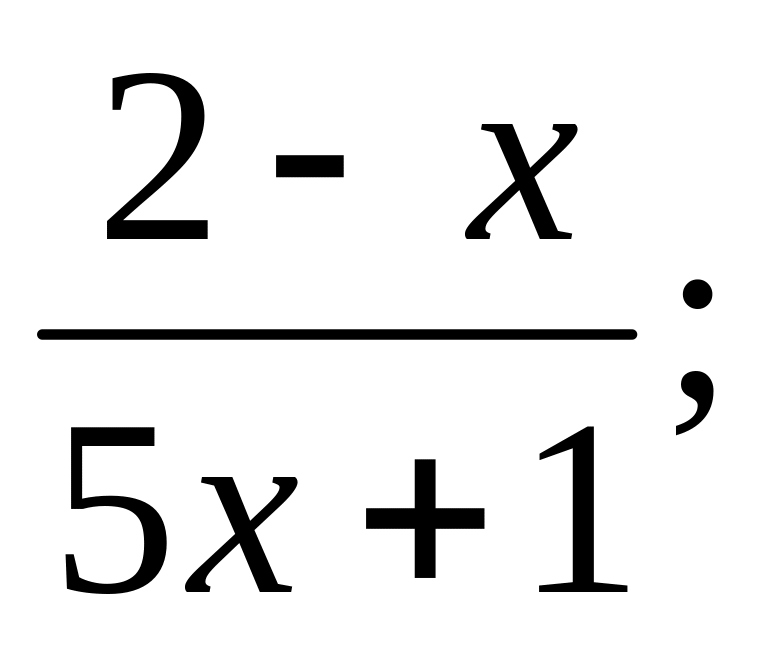
у =
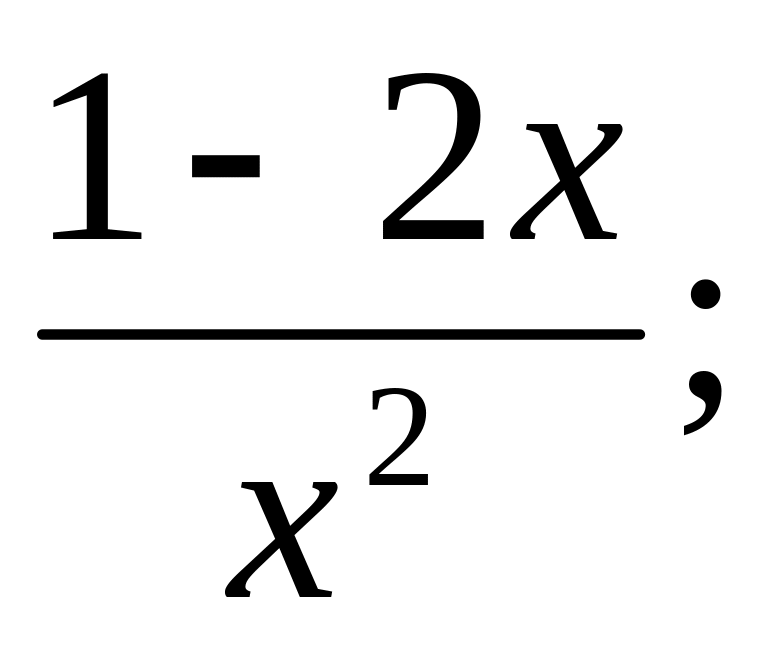
у =
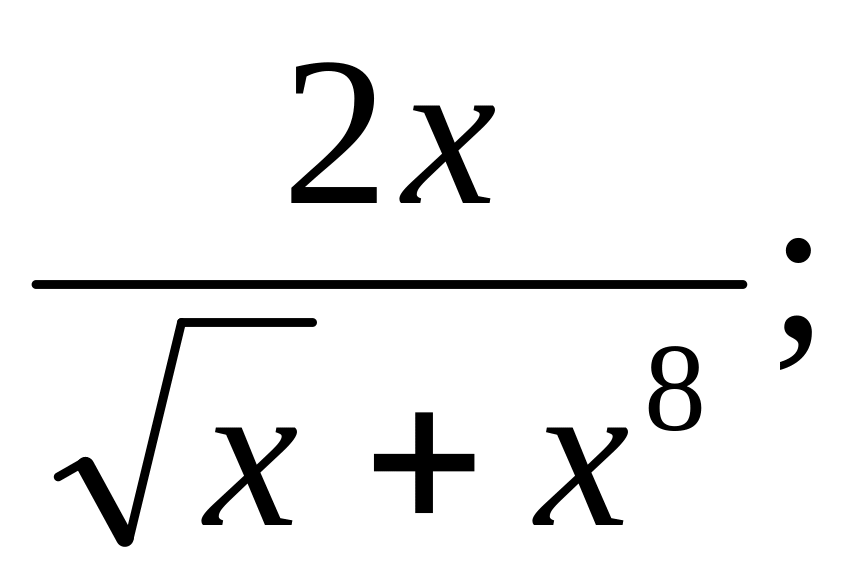
у =
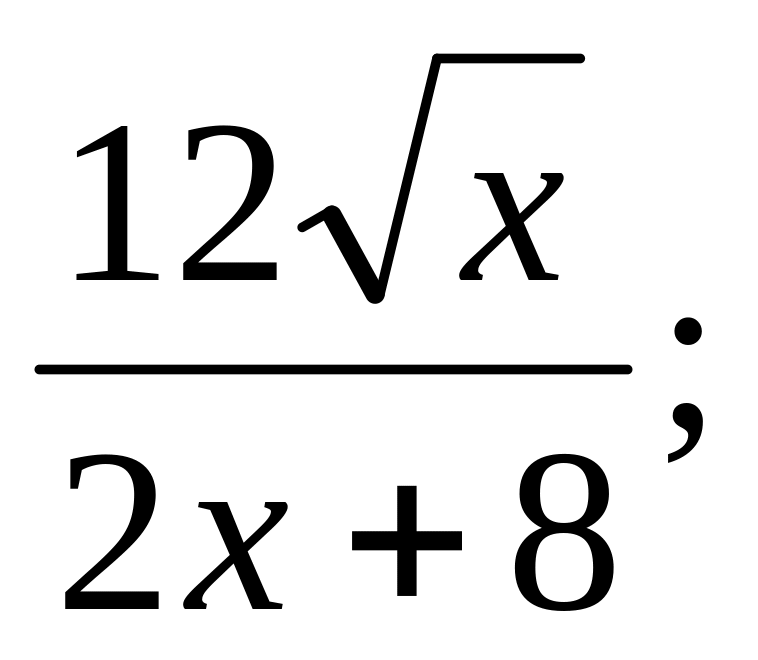
у =
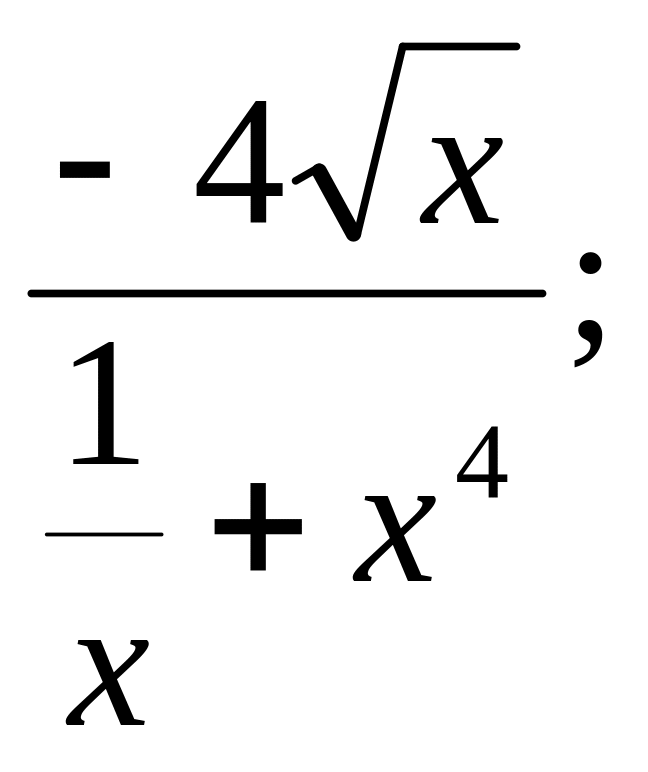
у =
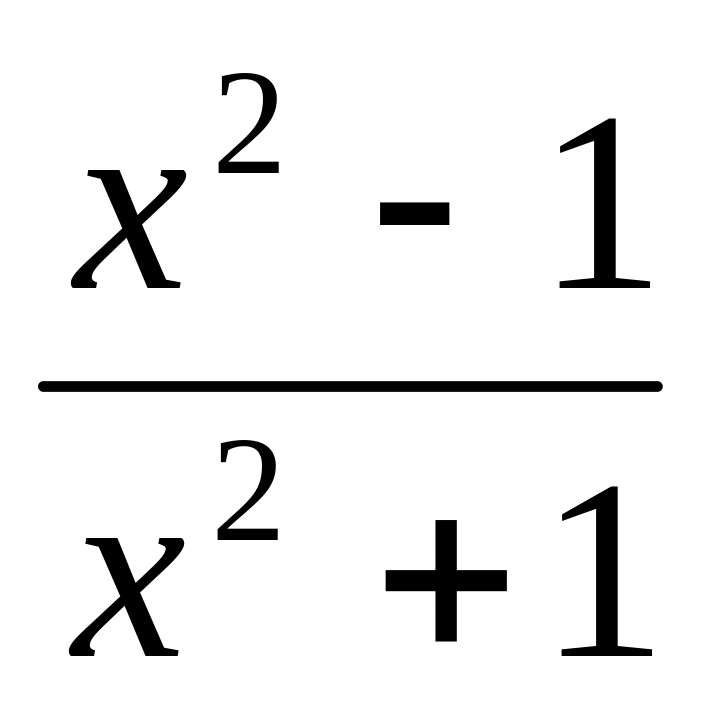 .
.
Обчислити значення похідної f(x) у зазначених точках:
f(x) = х2 +2x, х = -2; х =
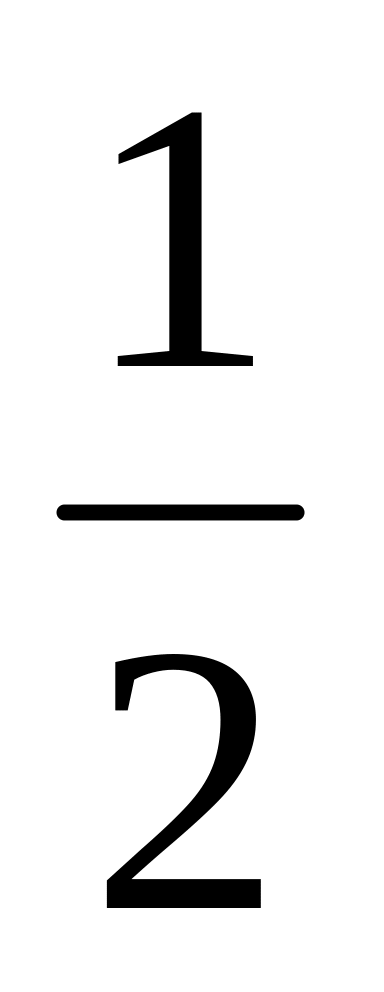 ;
;f(x) = х4 - 4x, х = 2; х = -1;
f(x) =
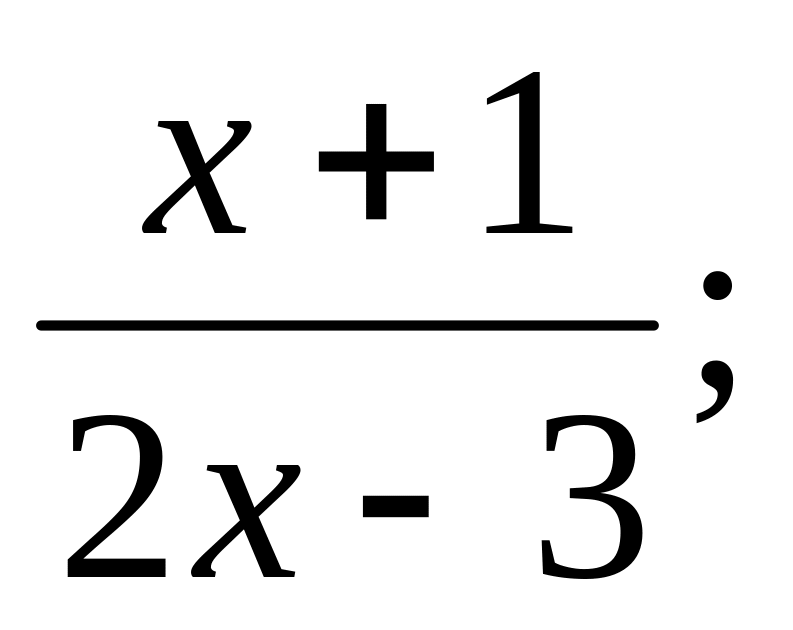 ,
х = 0; х = -3;
,
х = 0; х = -3;f(x) =
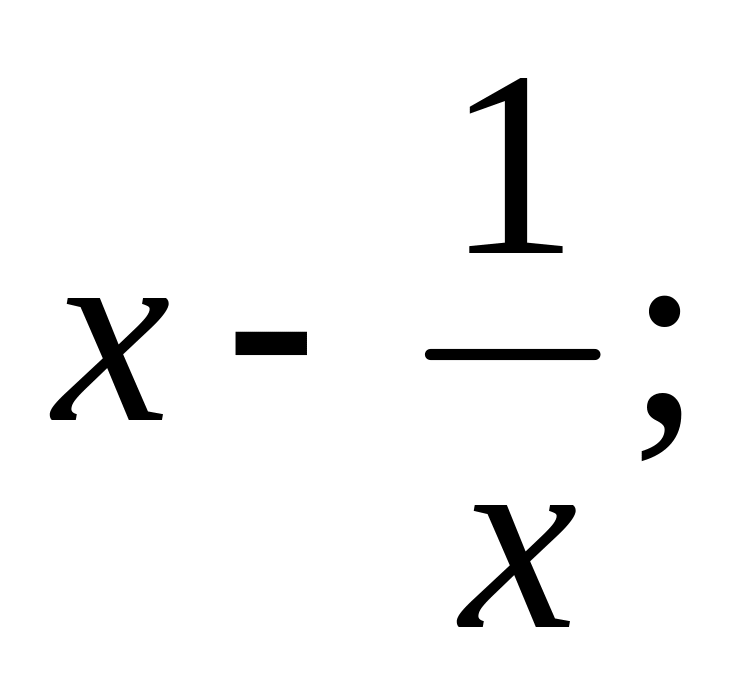 ,
х = -
,
х = -
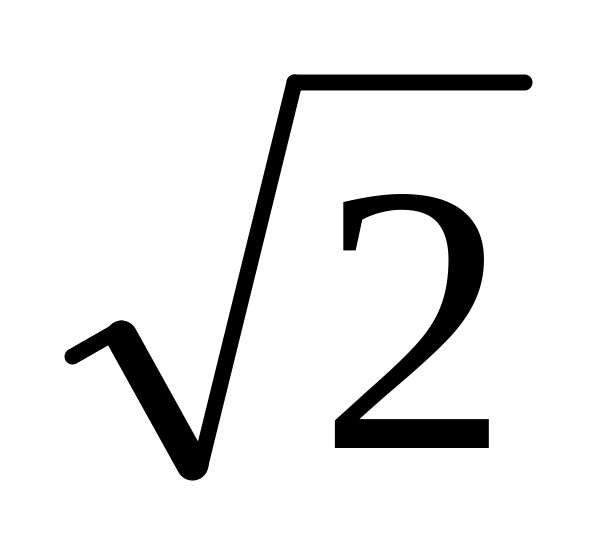 ;
х = 0,1.
;
х = 0,1.
Знайдіть значення х, для яких похідна функції дорівнює нулю:
f(x) = 3х2 - 6x;
f(x) =
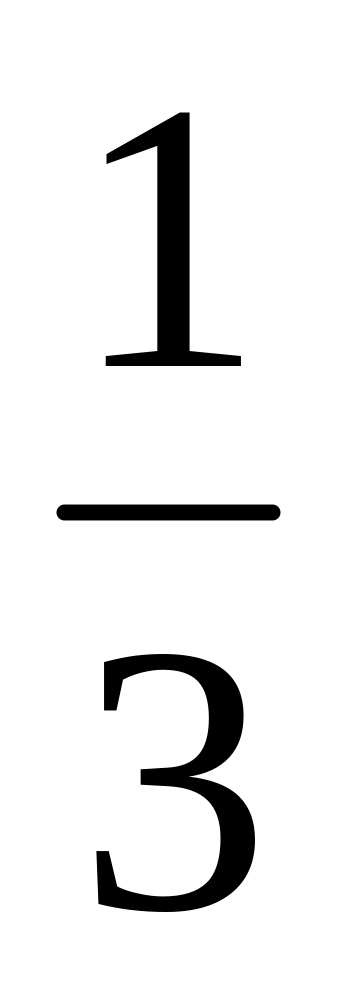 х3
+ х2
+ 5;
х3
+ х2
+ 5;f(x) = 12х +
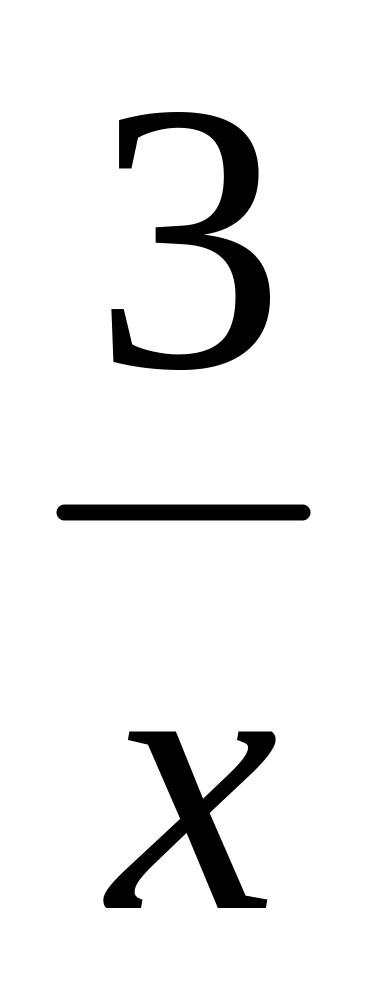 ;
;f(x) = - 2х2.
Розв'язати нерівність
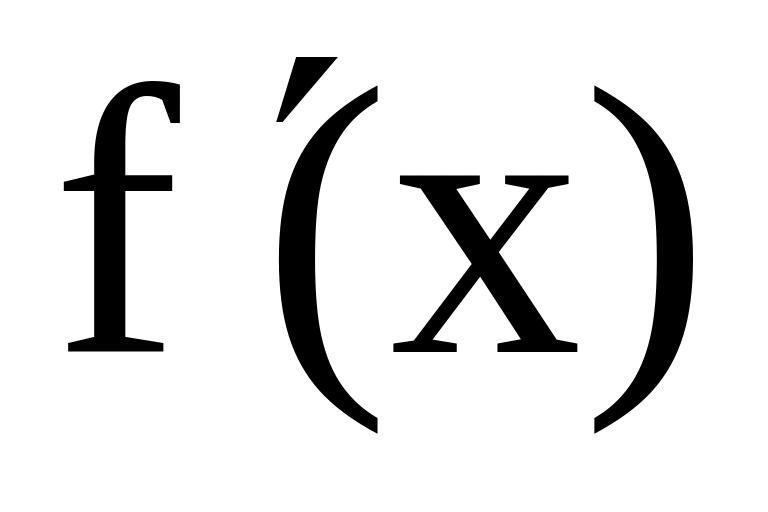 <
0, якщо:
<
0, якщо:
f(x) = 2х – х2; 2) f(x) = х3 + 3х2; 3) f(x) = 2х +
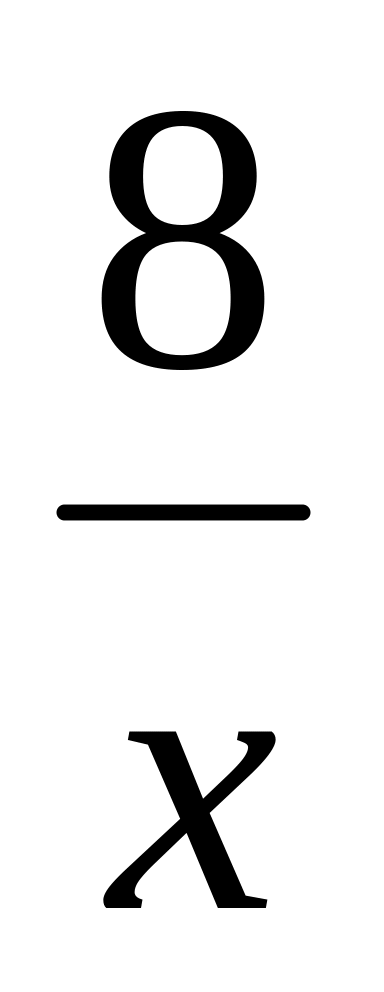 ;
4) f(x)
=
;
4) f(x)
=
 .
.
Знайдіть похідну в точці х = 1 наступних функцій:
f(x) =
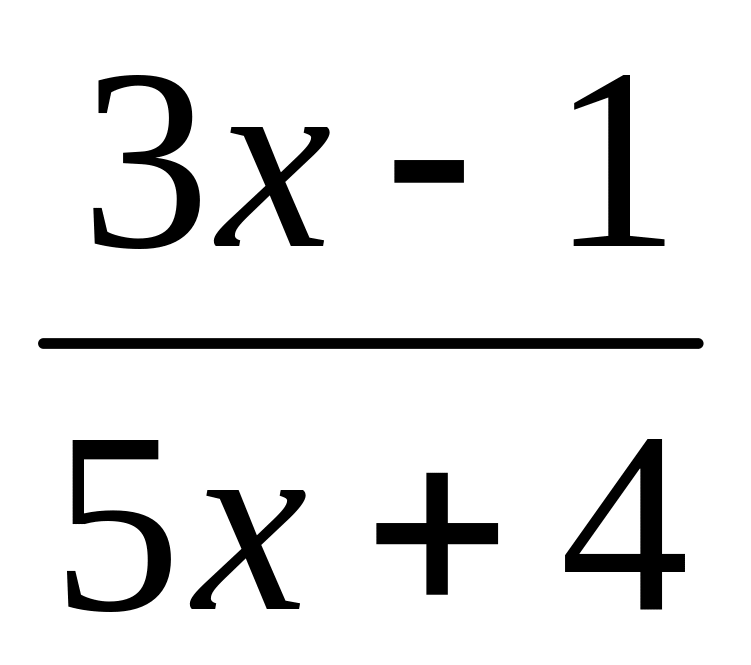 ;
;f(x) =
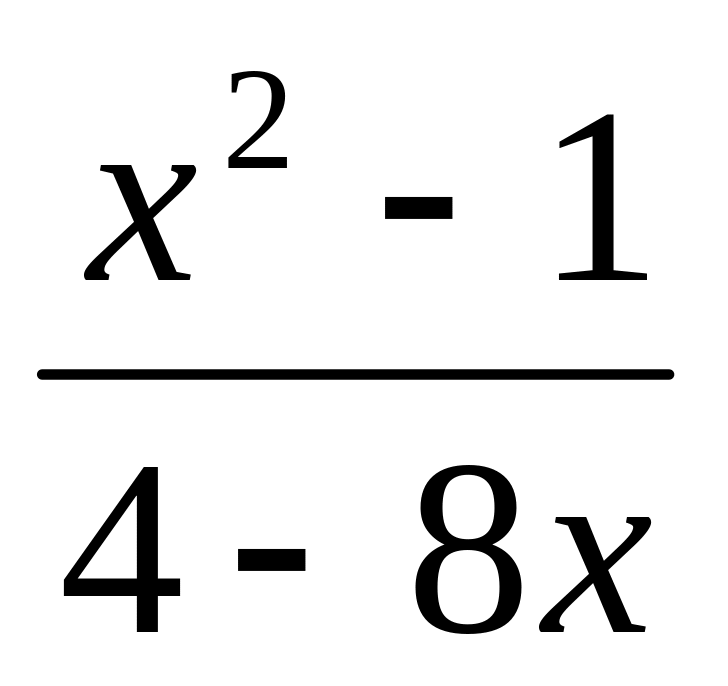 ;
;f(x) =
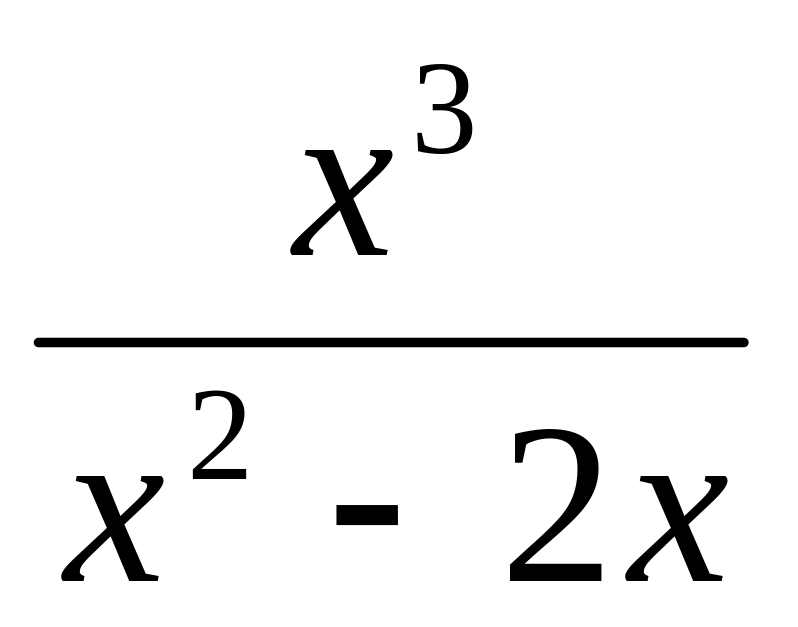 ;
;f(x) =
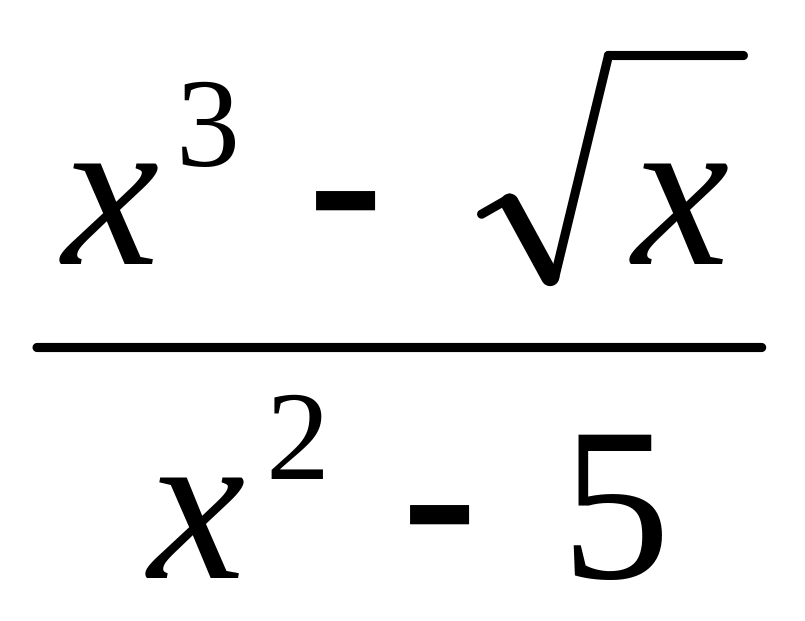 ;
;f(x) =
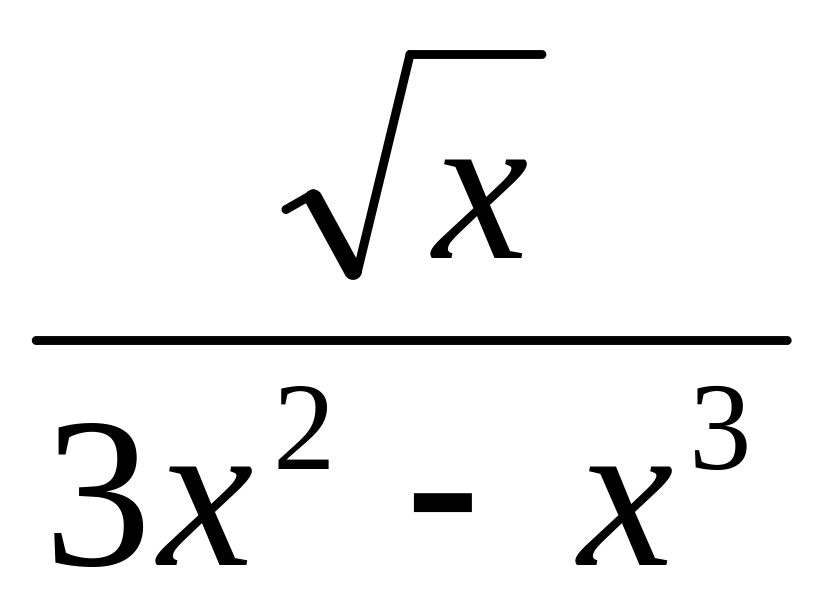 ;
;f(x) =
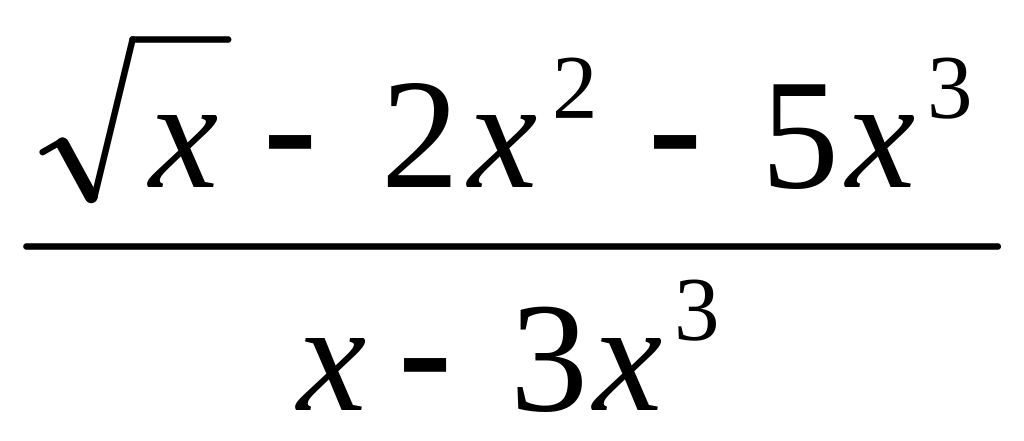 .
.

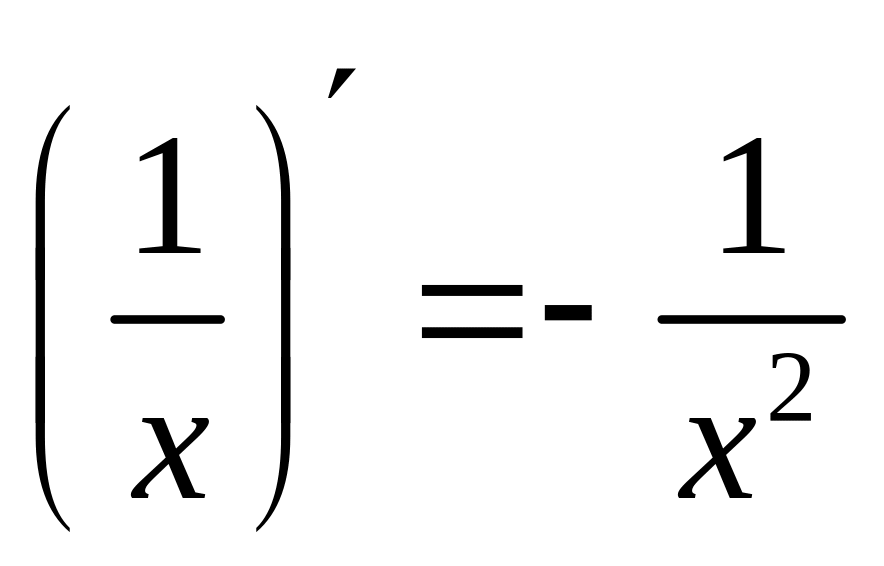 ,
х
0
,
х
0