Элементы дифференциального и интегрального исчислений

ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ

I. Производная характеризует быстроту изменения какой-либо величины y = f(x), зависящей от х , при изменении величины х. За меру этой скорости берется отношение Δf / Δх. При стремлении Δх к нулю величина Δf тоже стремится к нулю, но отношение Δf / Δх стремится к вполне определенному числу. Это число называется производной функции y=f(x) по аргументу х и обозначается как :

.

Дифференциалом dy называется приращение, которое получает функция y=f(x) при переходе от точки с координатой х в точку с

координатой х + dх. По определению это приращение равно:

dy= f(x+dх) - f(x) = f '(x)·dx

и, следовательно, определяется лишь значениями этой функции в начальной и конечной точках и не зависит от пути, по которому происходит переход.

1. Обратить внимание на следующие соотношения:

- средняя скорость; (1)

- (2)

мгновенная скорость, или просто скорость, равна первой производной радиус-вектора по времени t .

- модуль скорости. (3)

2. Приведём примеры, в которых физические величины связаны между собой операцией дифференцирования (вычисление производной называется дифференцированием):

- ускорение равно 1-й производной скорости по времени или 2-й производной радиус-вектора по времени; (произносятся как: дэ вэ по дэ тэ или дэ два эр по дэ тэ дважды).

- сила равна первой производной импульса тела по времени t;

- х-компонента силы, действующей на тело, равна со знаком минус первой производной потенциальной энергии тела U по координате х.

II. Примеры вычисления производной по формулам (2,3).

1. Радиус-вектор тела зависит от времени согласно закону: . Как зависит от времени скорость тела ?

РЕШЕНИЕ: в момент времени t+Δt имеем . Подставим значения и в (2):

Т.о., .

2. Пружинный маятник совершает колебания вдоль оси х по закону х(t)=А·sin(ω·t), где А и ω- постоянные. Чему равна скорость маятника в произвольный момент времени t?

РЕШЕНИЕ: смещение маятника от положения равновесия в момент времени t+Δt равно х(t+Δt)= А·sin(ω· (t+Δt)). Согласно (2-3):

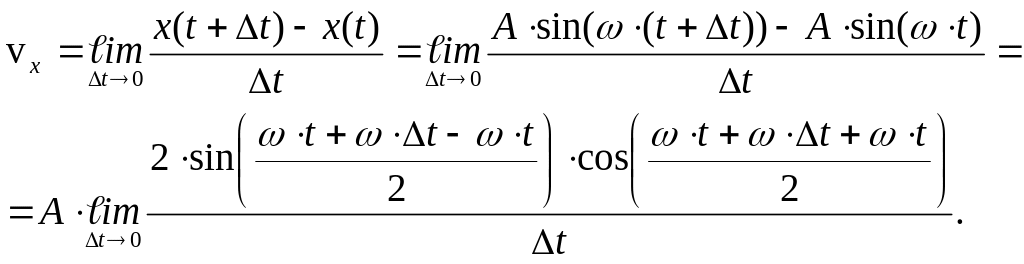
Умножим числитель и знаменатель дроби на ω и получим тогда:

Из теории пределов известно, что

И т.о., получаем

По аналогичной схеме вычисляются производные других функций.

III. В таблице 1 приведены формулы дифференцирования простых функций одной переменной.

Таблица 1.

№ п/п	Функция y=f(x)	Производная
1.	xn	nxn-1
2.	sinx	cosx
3.	cosx	-sinx
4.	ex	ex
5.	ℓnx	1/x

Общие правила дифференцирования функций.

1. Производная постоянной равна нулю: (y=c=const)'=0.

2. Постоянный множитель можно выносить за знак производной:

y=c·u(x); y'=[c·u(x)]'=c·u'(x).

3. Производная суммы конечного числа дифференцируемых

функций равна сумме производных этих функций:

y^'=[u(x)+v(x)+w(x)]'=u^'(x)+v^'(x)+w^' (x).

4. Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую функцию плюс произведение первой функции

на производную второй функции:

Примечание: правило 4 можно распространить на произвольное

число перемножаемых функций.

4. Производная дроби равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель – разность между произведением знаменателя на производную

числителя и произведением числителя на производную

знаменателя данной дроби, т.е.,

если , то :

.

4. Если имеем дело с так называемыми «вложенными» функциями, т.е. y=y(u), u=u(x), то производная вычисляется по правилу:

.

Примечание: правило 6 можно распространить на произвольное

число «вложенных» функций.

7. Если f = f(x,y,z) является функцией нескольких переменных

х,y,z, то производная функции f по одной из переменных

называется частной производной и обозначается как .

При вычислении частной производной, например по х, другие

переменные (y,z) считаются постоянными.

8. Полным дифференциалом функции f = f(x,y,z) называется полное приращение функции при переходе из начальной точки с координатами х ,y ,z в конечную точку с координатами

х+dx, y+dy, z+dz:

IV. ПРИМЕРЫ:

1. Вычислить модуль скорости тела v, если пройденный путь определяется выражением s=(5·t)⁶.

Решение: применяем правило 2 и п.1.табл. 1:

.

2. Вычислить ускорение тела а, если путь s=2·ℓnt.

Решение:

При расчёте применяем правило 2 и п.5 табл.1:

3. Вычислить ускорение тела а, если скорость v=ℓn(sint).

Решение: Применяем правило 6. Обозначим u=sint,

тогда v=ℓnu. и

4. Потенциальная энергия частицы задана выражением: Определить компоненты силы, действующей на частицу,:

Решение: применяем правило 7.

5. Потенциальная энергия частицы определяется выражением . Чему равен полный дифференциал потенциальной энергии?

Решение: применим правила 7,8 и п.1 табл.1:

V.КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется производной некоторой функции по аргументу, дифференциалом функции?

2. Расскажите схему расчёта производной некоторой функции y=f(x).

3. Запишите выражение для расчёта производной по х следующей функции y=U(x)·V(x)·W(x).

4. Запишите выражение для расчёта производной по х следующей функции у=U{V[W(x)]}.

5. Запишите выражение, связывающее быстроту изменения ускорения и радиус-вектор тела.

6. Запишите условие экстремума функции у=f(x).

VI. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Зависимость пути, пройденного точкой, от времени задана уравнением s=c·t + b·t³, где b=3м/с³. Найти ускорение точки через 0.5с после начала движения.

2. Тело движется прямолинейно, причем зависимость пути от времени задана в виде:

s = . Показать, что движение замедленное.

3. Координаты тела, движущегося в плоскости xoy, заданы как: x = k·t - b·t²; y = c·t + d, где k,b,c,d – постоянные. Найти скорость и ускорение тела в произвольный момент времени t.

4. Потенциальная энергия частицы имеет вид: ,

где α – постоянная, .

Найти действующую на частицу силу .