ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО

КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКАЯ

АКАДЕМИЯ (ИНЭКА)

Элементы высшей математики в применении к физике

Методические указания к самостоятельной работе по физике

г. Набережные Челны,

2006 г.

УДК 530 (077)

Элементы высшей математики в применении к физике.

Составитель Н.Б.Юнусов.

Методические указания к самостоятельной работе по физике.

г. Набережные Челны:

ИНЭКА, 2006 г., стр.33.

Методические указания предназначены для студентов дневной и заочной форм обучения.

Ил. – 13; Табл.- 2 ; Список лит. -5 наименов.

Рецензент:	д.т. н., проф. каф. ММИТЭ А.К.Розенцвайг

Печатается по решению научно-методического совета Камской государственной инженерно-экономической академии.

Камская государственная инженерно- экономическая

академия, 2006г.

СОДЕРЖАНИЕ

Стр.

I.	ПРИМЕНЕНИЕ ВЕКТОРОВ В ФИЗИКЕ	4
I I.	ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЙ В ПРИМЕНЕНИИ К ФИЗИКЕ К ФИЗИКЕ	13
III	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ	25
IV	МЕТОД ДИФФЕРЕНЦИРОВАНИЯ И ИНТЕГРИРОВАНИЯ	28
V	ЛИТЕРАТУРА	33

Цель настоящих методических указаний – представить в сжатой форме элементы векторного анализа, дифференциального и интегрального исчислений в объёме, достаточном для изучения курса физики в техническом вузе.

Применение векторов в физике

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. Вектор есть направленный отрезок, определяемый своей величиной (модулем) а ≡ , направлением в пространстве и точкой приложения. Направление вектора = а· задаётся единичным вектором , модуль которого │ │=1 (рис.1):

Вектор можно перемещать в пространстве в любом направлении параллельно самому себе.

Примеры		- радиус-вектор;		- перемещение;
векторов:		- скорость;		- ускорение;
		- сила;		- импульс.

2. Умножение вектора на действительное число k даёт вектор , направление которого определяется знаком числа k. Если k > 0, то направлен в ту же сторону, что и (рис. 2а). Если k < 0, то векторы и направлены в противоположные стороны (рис. 2б).

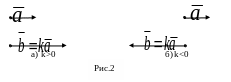
Примеры: , где -перемещение;

, где - гравитационная сила.

3. Два вектора и дают при сложении вектор , получающийся при использовании одного из двух приведённых на рис. 3 (а,б) способов.

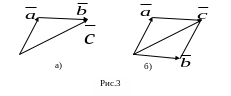
4. Разность двух векторов и можно получить из выражения и легко понять из рис. 4.

Следствия из п.п. 3,4:

а) ;

б) вектор (рис.5), показывающий изменение векторной величины от первоначального значения до конечного значения , называется приращением вектора ;

в) п.п.3 и 4 используются в т.н. принципе суперпозиции (независимости действия), когда необходимо определить результирующую векторную величину: ; ; , где - результирующие скорость, сила и напряжённость поля, соответственно.