МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Московский государственный университет экономики, статистики и информатики
МХИТАРЯН С.В.
Маркетинговые исследования рынка с использованием ППП Statistica
Москва, 2009
Мхитарян С.В. Практикум по дисциплине «Маркетинговые исследования рынка с использованием ППП Statistica». / Моск. гос. ун-т экономики, статистики и информатики. – М., 2009.
© Мхитарян Сергей Владимирович, 2009 г.
© Московский государственный университет экономики, статистики и информатики, 2009 г.
Содержание
1. Основы работы с программой 4
2. Анализ временных рядов и прогнозирование 4
2.1. Модель ARIMA – АРПСС: Авторегрессии и проинтегрированное скользящее среднее. 5
2.2. Модель Interrupted ARIMA – Прерванная ARIMA (ARIMA с интервенцией). 10
2.3. Модель Distributed Lags Analysis – Анализ распределенных лагов. 14
3. Изучение взаимосвязи маркетинговых показателей 16
4. Выявление маркетинговых макрохарактеристик 22
5. Сегментирование в маркетинге (без отклика) 26
5.1. Модель Joining (tree clustering) – Иерархические агломеративные методы. 27
5.2. Модель K-means clustering – Метод K-средних. 29
6. Сегментирование в маркетинге (с откликом) 31
7. Задачи для самостоятельной работы 37
Список литературы и ссылки на ресурсы Интернет 50
1. Основы работы с программой
В кратком описании статистических модулей будут приводиться примеры, устанавливающиеся при инсталляции системы из директории \examples\. Рассматриваются задачи для версии Statistica 6.0 и выше.
Запустите систему Statistica, в переключателях модулей выберите необходимый модуль для обработки.
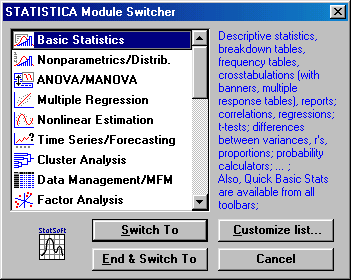
2. Анализ временных рядов и прогнозирование
Анализ временных рядов позволяет выявить скрытые закономерности во временных рядах, построить модели этих закономерностей, провести прогнозирование.
В переключателе модулей выберите модуль Time Series Analysis / Forecasting - Анализ временных рядов и прогнозирование.
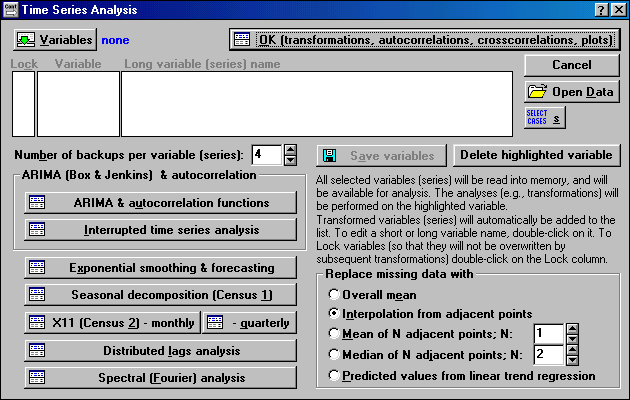
Откройте данные - Open Data,
Выберите переменные – Variables,
Запустите необходимую модель обработки.
2.1. Модель arima – арпсс: Авторегрессии и проинтегрированное скользящее среднее.
Модель ARIMA – АРПСС: Авторегрессии и проинтегрированное скользящее среднее относится к адаптивным методам прогнозирования, которые позволяют строить самокорректирующие экономико-математические модели. Эти модели способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге и учета различной информационной ценности уровней ряда. Информационная ценность последних наблюдений в экономических рядах обычно значительно выше, чем более ранних, так как информация очень быстро теряет свою актуальность в силу высокой турбулентности экономической среды.
Откройте в стартовой панели модуля файл Series_g.sta.
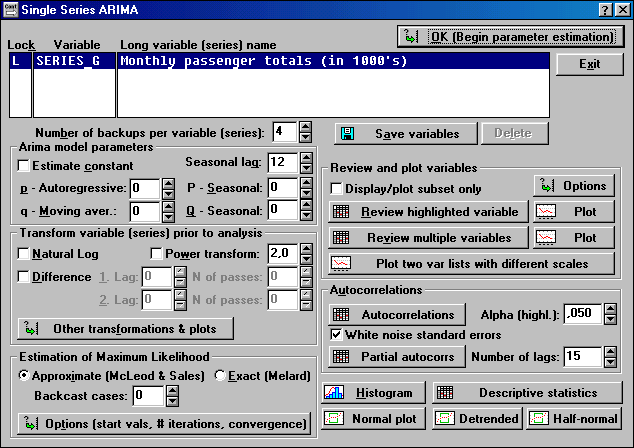
В окне Time Series Analysis откройте модуль ARIMA & autocorrelation functions – АРПСС и автокорреляционные функции.
В блоке Arima model parameters – устанавливаются параметры модели:
Estimate constant – учет в модели константы,
Sesonal lag – сезонный лаг,
Основные параметры модели:
p – Autoregressive – регулярный параметр авторегрессии,
P – Sesonal – сезонный параметр авторегрессии,
q – Mouving average – регулярный параметр скользящего среднего,
Q - Sesonal – сезонный параметр скользящего среднего.
Большинство наблюдаемых моделей стационарных рядов (без учета тенденции и сезонности) может быть отнесены с высокой степенью точности к одному из пяти классов:
модели авторегрессии с одним параметром: p=1, q=0,
модели авторегрессии с двумя параметрами: p=2, q=0,
модели скользящего среднего с одним параметром: p=0, q=1,
модели скользящего среднего с двумя параметрами: p=0, q=2,
модели авторегрессии с одним параметром и скользящего среднего с одним параметром: p=1, q=1.
Параметры модели подбираются эмпирически, качество различных моделей сравнивается по характеристикам остатков – разности смоделированных и фактических значений. В хорошей модели взаимосвязь остатков низкая, графики автокорреляционной и частной автокорреляционной функции не превышаю допустимых границ.
Для сезонных моделей АРПСС.
После применения дополнительных преобразований - Other transformations & plots, исключающих сезонность - получение разности с соответствующими лагами, сезонные параметры P и Q могут быть определены для каждого из вышеперечисленных классов моделей.
В блоке Transform variable (series) prior to analysis – устанавливаются параметры изменения переменных до обработки:
Natural Log – натуральное логарифмирование,
Power transform – возведение в соответствующую степень,
Difference – разность с соответствующим лагом (Lag), выполняющаяся указанное количество раз (N of passes), разность - важный параметр модели,
Other transformations & plots – другие преобразования и графики.
В блоке Review and plot variables можно просмотреть переменные и построить их графики.
В блоке Autocorrelations можно посмотреть автокорреляционную (Autocorrelations) и частную автокорреляционную (Partial autocorrs) функции, это необходимо для определения параметров модели и изменения параметров переменных до обработки.
После настроек модели (для нашего примера это p=P=0, q=Q=1, Natural Log - включен, Difference – включен, Lag1=1, N of passes=1, Lag2=12, N of passes=1),
нажмите кнопку расчета – OK (Begin parameter estimation).
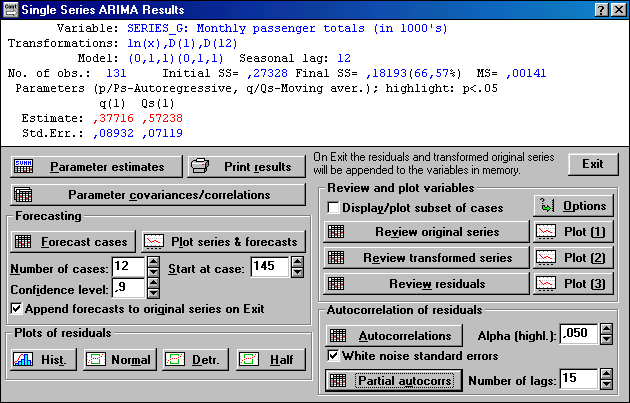
В верхней части окна – информация о модели и оценках ее параметров.
Блок Forecasting – прогнозирование. Задает параметры прогноза: количество случаев прогноза, с какого случая строить прогноз, доверительный интервал,
кнопки Forecast cases – выводит таблицу прогнозных значений и доверительного интервала, Plot series & forecast – выводит график исходного ряда и прогноза.
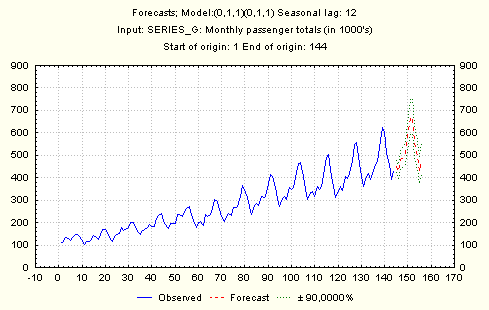
Блоки Plots of residuals и Autocorrelation of residuals выводят различные гистограммы и графики остатков и графики автокорреляционной и частной автокорреляционной функций.
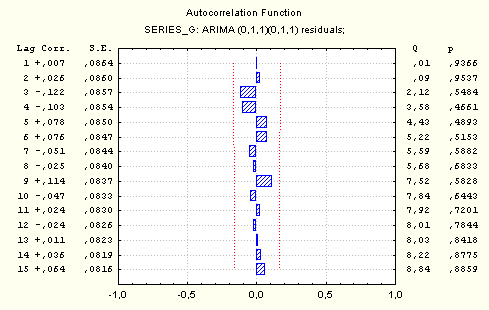
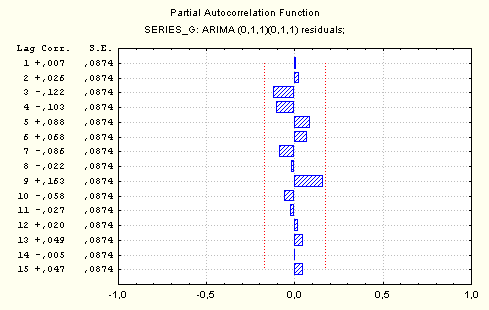
На графиках нашего примера автокорреляционная и частная автокорреляционная функция не превышают граничных значений, что говорит об адекватности выбранной модели.