6.2. Кут між двома прямими у просторі. Умови паралельності і перпендикулярності прямих у просторі

Нехай прямі і задані канонічними рівняннями (2.35).

тоді

тоді

Кут між прямими і дорівнює куту між їх напрямними векторами і (рис. 12).

Кут між прямими і , які задані канонічними рівняннями знаходять за формулою:
	(2.39)
звідки умова паралельності прямих і ; умова перпендикулярності прямих і

Знайти кут між прямими, які задані рівняннями:

: :

Розв'язання.

Знайдемо напрямний вектор прямої .

Площина, задана рівнянням має нормальний вектор

а площина, задана рівнянням має нормальний вектор

Напрямний вектор прямої дорівнює:

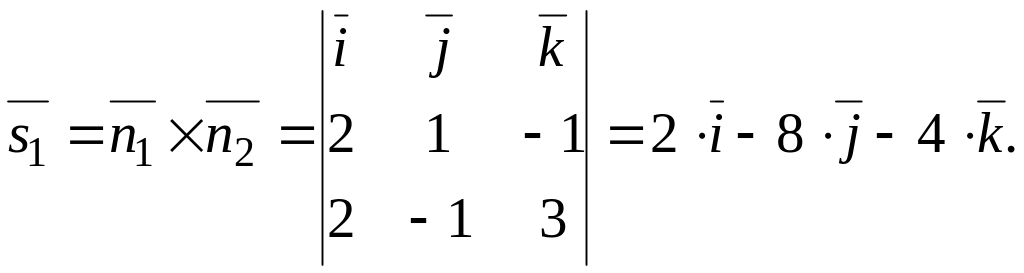
Із параметричних рівнянь прямої отримаємо її напрямний вектор

тоді за формулою (2.39):

звідки Відповідь.

6.3. Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини

Кутом між прямою і площиною називається, як відомо із шкільного курсу геометрії, кут між цією прямою і її проекцією на площину. Нехай пряма і площина перетинаються в точці (рис. 22). Із довільної точки прямої опустимо перпендикуляр тоді пряма проекція прямої на площину . Звідси, кут між прямою і площиною .

Нехай пряму задано канонічним рівнянням ,

тоді напрямний вектор прямої; площину задано загальним рівнянням тоді її нормальний вектор

Косинус кута між векторами і дорівнює: але з тоді

кут між прямою , заданою рівнянням , і площиною , заданою рівнянням знаходять із формули: (2.40) звідки: умова паралельності прямої і площини , умова перпендикулярності прямої і площини .

Зразок виконання контрольного завдання №2.

Дано координати вершин піраміди :

Знайти: 1) рівняння граней і ;

2) кут між гранями і ;

3) рівняння ребра

4) кут між ребром і гранню ;

5) відстань від точки до площини .

Розв'язання.

1) Рівняння граней і знайдемо за формулою (2.29).

Р івняння грані :

загальне рівняння

грані .

Рівняння грані :

загальне рівняння грані .

Відповідь. загальне рівняння грані ,

загальне рівняння грані .

[ Продовження зразка виконання контрольного завдання №2.]

2) Кут між гранями і знайдемо за формулою (2.30).

тоді

На рисунку (23) побудовано лінійний який дорівнює двогранному куту між гранями і .

Відповідь. Кут між гранями і дорівнює

3) Рівняння ребра , де знайдемо за формулою (2.37):

Відповідь. канонічне рівняння ребра .

4) Кут між ребром і гранню знайдемо за формулою (2.40).

напрямний вектор ребра , тоді:

звідки

На рисунку (23) побудовано лінійний який дорівнює

куту між ребром і гранню .

Відповідь. Кут між ребром і гранню дорівнює

5) Проведемо тоді відстань від точки до площини обчислимо за формулою (2.34):

Відповідь. од.

Зразки виконання контрольного завдання №3.

Знайти точку , симетричну до точки відносно прямої:

Розв'язання.

Нехай точка симетрична до точки відносно прямої заданої рівнянням:

(рис. 24). Тоді причому точка належить прямій

Р озглянемо площину яка проходить через відрізок і перпендикулярна до прямої

Знайдемо координати точки , яка є серединою відрізка , як точки перетину площини і перпендикулярної до неї прямої Для цього складемо рівняння площини . Вектор який є напрямним векто-ром для прямої перпендикуляр-ний до площини . Тоді, за формулою (2.26), рівняння площи-ни , якій належить точка має вигляд:

Знайдемо координати точки , як точки перетину площини і прямої

тоді:

Звідси, середина відрізка має координати:

Координати точки знайдемо за формулами середини відрізка:

Відповідь.

Знайти точку , симетричну до точки відносно площини, заданої рівнянням:

Розв'язання.

Нехай точка симетрич-на до точки відносно площини заданої рівнянням (рис. 25).

Тоді причому точка належить площині

Знайдемо координати точки , яка є серединою відрізка , як точки перетину площини і перпендикулярної до неї прямої Для цього складемо рівняння прямої Вектор перпендикулярний до площини , є напрямним вектором для прямої

Канонічне рівняння прямої яка проходить через точку і має

напрямний вектор складемо за формулою (2.35):

Знайдемо координати т. – точки перетину площини і прямої :

тоді:

Отже, середина відрізка має координати:

Координати точки знайдемо, використовуючи формули середини відрізка:

Відповідь.