§ 4. Пряма на площині

Нормальним вектором прямої на площині називається будь-який ненульовий вектор, перпендикулярний до цієї прямої (рис. 9).

Напрямним вектором прямої на площині називається вектор, який паралельний до прямої або співпадає з нею (рис. 9) .

4.1. Різні види рівнянь прямої на площині

1) Нехай пряма проходить через точку і перпендикулярна до вектора , точка довільна точка прямої .

Тоді вектор перпендикулярний до вектора , тобто Записавши останню рівність у координатній формі отримаємо

рівняння прямої з нормальним вектором , яка проходить через точку :
.	(2.13)

2) Розкривши дужки у рівнянні прямої (2.13) і позначивши отримаємо

загальне рівняння прямої на площині:
.	(2.14)

3) Записавши у координатній формі умову колінеарності вектора і напрямного вектора прямої отримаємо

канонічне рівняння прямої на площині:
	(2.15)

Рівняння (2.15) часто називають рівнянням прямої на площині, яка проходить через точку і паралельна вектору .

4) Розглянувши векторну рівність отримаємо

векторне параметричне рівняння прямої на площині:
	(2.16)
де параметр (змінна величина).

5) Запишемо векторне рівняння (2.16) у координатній формі, прирівнявши координати рівних векторів та .

Отримаємо параметричні рівняння прямої , яка проходить через точку і має напрямний вектор :
	(2.17)

6) Рівняння прямої, яка проходить через дві задані точки і
	(2.18)

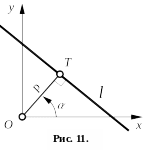
7) Рівняння прямої у відрізках на осях (рис. 10):
	(2.19)

8) Рівняння прямої, яка проходить через задану точку і має заданий кутовий коефіцієнт
,	(2.20)
де (рис. 10).

9) Нормальне рівняння прямої :
	(2.21)
де (рис. 11).

4.2. Дослідження загального рівняння прямої

1) Якщо то пряма перетинає осі координат в точках із координатами:

2) пряма, задана рівнянням , проходить через початок координат;

3) пряма, задана рівнянням , паралельна осі ;

4) і пряма, задана рівнянням , є віссю ;

5) пряма, задана рівнянням , паралельна осі ;

6) і рівняння осі

Якщо скласти одне з рівнянь (2.13–2.20) прямої на площині, то будь-яке інше рівняння прямої з даного переліку можна знайти за допомогою нескладних тотожних алгебраїчних перетворень.