УКРАЇНА

Національний університет біоресурсів і природокористування України

Ніжинський агротехнічний інститут

Кафедра природничо-фундаментальних дисциплін

ВИЩА МАТЕМАТИКА

Модуль 2. Елементи аналітичної геометрії

Методичні вказівки і контрольні завдання

для самостійної роботи

Укладач: Муквич М.М.

Ніжин –2013

УДК 514.123 (073)

Рекомендовано до друку Вченою Радою

Ніжинського агротехнічного інституту

Національного університету біоресурсів і природокористування України

Протокол №2 від 25 жовтня 2012 р.

Укладач: М.М. Муквич, к.т.н., доцент кафедри природничо-фундаментальних дисциплін Ніжинського агротехнічного інституту

Рецензенти:

В.М. Лось, к. ф.-м. наук, доцент, завідувач кафедри вищої та прикладної математики Чернігівського державного технологічного університету

Н.В. Майбородіна, к. ф.-м. наук, старший викладач кафедри природничо-фундаментальних дисциплін Ніжинського агротехнічного інституту

ВИЩА МАТЕМАТИКА. Модуль 2. Елементи аналітичної геометрії: методичні вказівки та контрольні завдання для самостійної роботи / Укл.: М.М. Муквич. – Ніжин: Видавець ПП Лисенко М.М, 2013. – 56 с.

Наведено короткі теоретичні відомості розділу «Елементи аналітичної геометрії», індивідуальні контрольні завдання та зразки їх розв’язань.

Для самостійної роботи студентів інженерних напрямів підготовки.

© Укл. Муквич М.М., 2013

© ПП Лисенко М.М.,

ВСТУП

Це навчальне видання є продовженням методичних вказівок для самостійної роботи студентів інженерних напрямів підготовки "ВИЩА МАТЕМАТИКА. Модуль 1. Елементи лінійної та векторної алгебри", і призначене для організації самостійної роботи студентів-першокурсників.

У навчальному виданні розглянуто контрольні завдання згідно тем індивідуальних (розрахунково-графічних) завдань другого модуля у програмах з навчальної дисципліни «Вища математика», для підготовки фахівців ОКР «бакалавр» напрямів підготовки:

6.100101 «Енергетика та електротехнічні системи в агропромисловому комплексі» у вищих навчальних закладах II – IV рівнів акредитації Міністерства аграрної політики України (автори Ю.Б. Гнучій, Н.Г. Батечко, О.Ю. Дюженкова, Р.Ф. Овчар, О.І. Завгородній. – Київ: Аграрна освіта, 2010);

6.100102 «Процеси, машини та обладнання агропромислового виробництва» у вищих навчальних закладах II – IV рівнів акредитації Міністерства аграрної політики України (автори Ю.Б. Гнучій, Н.Г. Батечко, О.Ю. Дюженкова, Р.Ф. Овчар, О.І. Завгородній, В.І. Кравець. – Київ: Аграрна освіта, 2010).

Для самостійного контролю при засвоєнні навчального матеріалу необхідно використовувати контрольні запитання, які подано в методичних вказівках.

Початок і кінець наведеного розв’язку завдання позначено символами та відповідно.

Модуль 2. Елементи аналітичної геометрії.

(Короткі теоретичні відомості)

§ 1. Лінії на площині та їхні рівняння.

Лінію на площині можна задати рівнянням: (2.1) яке задовольняють координати всіх точок даної лінії і не задовольняють координати жодної точки, яка не лежить на цій лінії.

Розглянемо коло з центром радіуса задане рівнянням:

Точка належить заданому колу, бо при підстановці її координат у дане рівняння воно перетворюється у правильну рівність.

Точка не належить заданому колу, бо при підстановці в дане рівняння її координат отримаємо:

Щоб знайти координати точок перетину двох ліній на площині, заданих рівняннями , необхідно розв’язати систему рівнянь:

В аналітичній геометрії є дві основні задачі:

1) задано геометричні властивості лінії, тоді потрібно скласти її рівняння (1);

2) задано рівняння лінії (1), потрібно визначити її властивості.

1.1. Полярна система координат

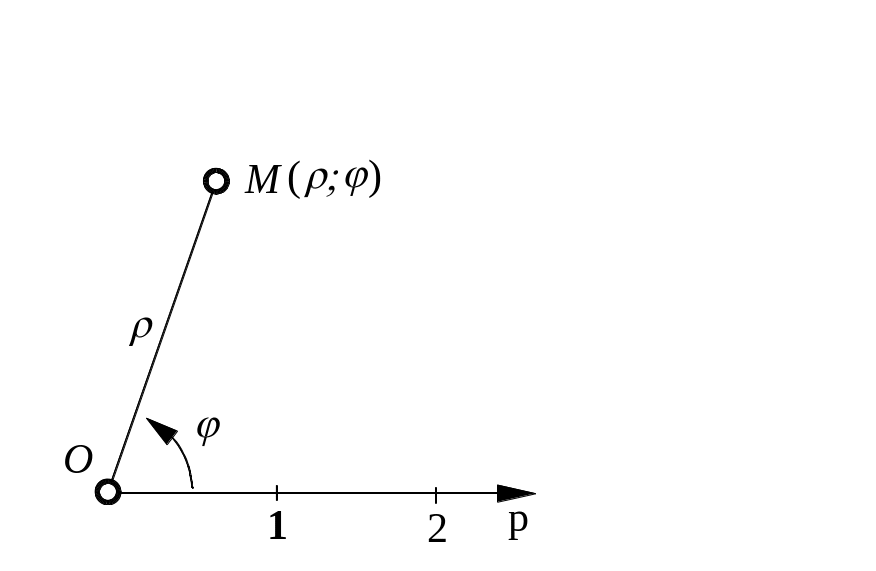
Полярна система координат задається точкою полюсом, променем який виходить із полюса і називається полярною віссю (рис. 1). Полярними координатами точки називаються числа і . Позначення: полярний радіус, полярний кут,

Рис. 1.

Формули переходу від декартових координат до полярних мають вигляд: (2.2) де

Формули переходу від полярних координат до декартових: (2.3)

Рівняння називається рівнянням лінії в полярних координатах (або полярним рівнянням лінії), якщо його задовольняють координати будь-якої точки лінії і не задовольняють координати жодної точки, яка не лежить на цій лінії.

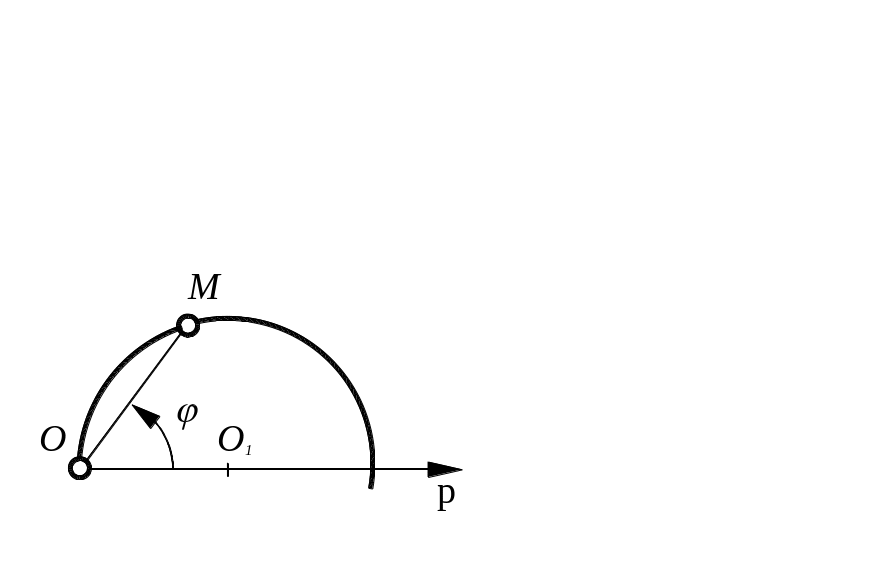Рівняння кола з центром на поляр-ній осі і радіусом (рис. 2) має вигляд:

Рис. 2.

1.2. Параметричні рівняння лінії

Рівняння виду: (2.4) називають параметричними рівняннями лінії на площині в декартовій прямокутній системі координат, якщо для кожного значення параметра із заданого проміжку: точка належить даній лінії. параметр (змінна величина), який набуває значень із деякого проміжку.

Параметричні рівняння кола з центром і радіусом

мають вигляд:

2.1.3. Векторне рівняння лінії

Рівняння виду: н (2.5) азивають векторним рівнянням лінії на площині.

Будь-яку точку лінії (рис. 3) можна задати вектором тоді д (2.5*) е орти ортонормованого базису на площині.

Векторному рівнянню в прямокутній системі координат відповідають два скалярних параметричних рівняння:

Векторне рівняння кола з центром і радіусом має вигляд: