Практическое занятие №6 Расчет надежности системы с поэлементным резервированием.

При поэлементном резервировании резервируются отдельно элементы системы. Определим количественные характеристики надежности системы.

Запишем вероятность отказа i - ой группы. Имеем

(6.1)

где q_ij(t) - вероятность отказа элемента Э_ij на интервале времени (0, t).

Запишем вероятность безотказной работы j-ой группы. Получим

, (6.2)

где P_ij(t) - вероятность безотказной работы элемента Э_ij на интервале времени (0,t); m_i - кратность резервирования элемента j-ой группы.

Запишем вероятность безотказной работы системы с поэлементным резервированием

или

(6.3)

Для равнонадежных элементов системы и m_i=m=const имеем

(6.4)

(6.5)

Если

(6.6)

то формула (6.З) примет вид

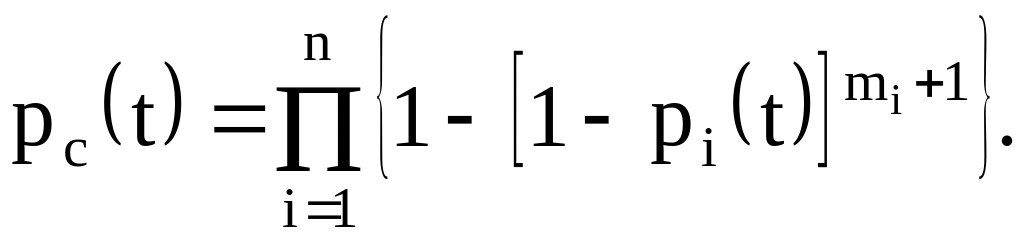(6.7)

При экспоненциальном законе надежности, когда P_i(t)=e^{-i t},

(6.8)

В этом случае формула (6.5) примет вид

(6.9)

а среднее время безотказной работы системы определяется соотношением

(6.10)

Подставляя (6.9) в (6.10),получим

(6.11)

где

Практическое занятие № 7 Резервирование с дробной кратностью и постоянно включенным резервом.

Резервированная система состоит из l отдельных систем. Для ее нормальной работы необходимо, чтобы исправными были не менее чем h систем.

Кратность резервирования такой системы равна

(7.1)

Предполагается, что основные и все резервные системы равнонадежны.

Вероятность безотказной работы резервированной системы:

(7.2)

где

(7.3)

Здесь - вероятность безотказной работы основной системы или любой резервной системы; l - общее число основных и резервных систем; h - - число систем, необходимых для нормальной работы.

Будем предполагать, что для любой отдельно взятой системы справедлив экспоненциальный закон надежности, т.е.

(7.4)

Определим среднее время безотказной работы системы. Имеем

. (7.5)