Розв’язування систем лінійних рівнянь методом Гаусса

Метод Гаусса – метод послідовного виключення невідомих.

Розглянемо систему лінійних рівнянь із невідомими (6):

Поставимо у відповідність даній системі рівнянь основну матрицю системи лінійних рівнянь: ,

та розширену матрицю системи:

Метод Гаусса полягає в тому, що за допомогою елементарних перетворень над рядками розширеної матриці системи лінійних рівнянь матрицю зводять до трапецієподібного вигляду, коли елементами уявної головної діагоналі матриці є деякі числа , а усі елементи під уявною головною діагоналлю дорівнюють 0: .

При цьому легко визначити ранг основної та розширеної матриці, який дорівнює кількості рядків матриці, які мають принаймні один ненульовий елемент.

Матриці відповідає східчаста система лінійних рівнянь:

із якої послідовно знаходять невідомі: .

До елементарних перетворень над рядками матриці належать дії:

1. Перестановка місцями двох рядків матриці;

2. Множення кожного елемента рядка на один і той самий, відмінний від нуля множник;

3. Додавання до елементів рядка відповідних елементів іншого рядка, помножених на одне і те саме число.

При дослідженні системи лінійних рівнянь на сумісність (тобто наявність розв’язків) використовують критерій сумісності системи лінійних рівнянь із невідомими, формулювання якого подано нижче.

1. Для того, щоб система лінійних рівнянь із невідомими була сумісною (тобто мала розв’язки), необхідно і достатньо, щоб ранг її основної матриці дорівнював рангу розширеної матриці .

2. Якщо ранг основної матриці дорівнює рангу розширеної матриці і дорівнює числу невідомих то система лінійних рівнянь має єдиний розв’язок (тобто є визначеною).

3. Якщо ранг основної матриці дорівнює рангу розширеної матриці , але менший числа невідомих то система лінійних рівнянь має нескінченну множину розв’язків (тобто є невизначеною).

Зразок виконання контрольного завдання №3.

Методом Гаусса розв'язати систему або переконатись у її несумісності:

а)

Розв’язання.

Розглянемо розширену матрицю системи лінійних рівнянь:

Для зручності перетворень виберемо одиничний елемент із першого стовпця матриці: .

Використовуючи елементарні перетворення над рядками розширеної матриці , перетворимо її елементи так, щоб усі елементи першого стовпця, крім елемента , стали нулями. Для цього всі елементи першого рядка матриці:

помножимо на і додамо до відповідних елементів другого рядка;

помножимо на і додамо до відповідних елементів третього рядка;

помножимо на і додамо до відповідних елементів четвертого рядка.

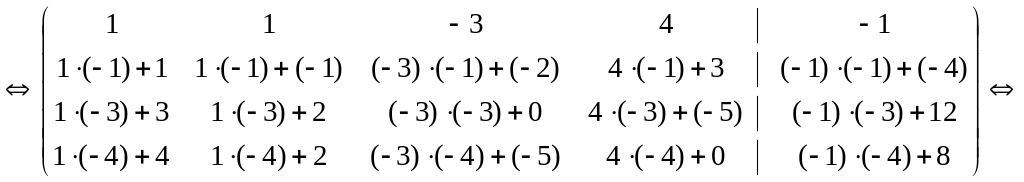
Для зручності поміняємо місцями й та й рядки:

Перетворимо елементи матриці так, щоб усі елементи другого стовпця «під елементом» стали нулями. Для цього всі елементи другого рядка матриці помножимо на і додамо до відповідних елементів третього та четвертого рядка:

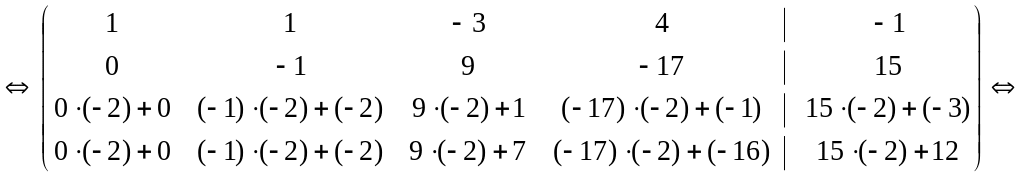
Перетворимо матрицю так, щоб елемент став нульовим.

Найменше спільне кратне чисел та дорівнює: Тому помножимо усі елементи четвертого рядка матриці на

Елементи третього рядка матриці помножимо на і додамо до відповідних елементів четвертого рядка:

тобто ранг основної матриці дорівнює і дорівнює рангу розширеної матриці , і дорівнює числу невідомих тому за теоремою Кронекера-Капеллі система лінійних рівнянь має єдиний розв’язок.

Запишемо систему лінійних рівнянь:

Із останнього рівняння системи маємо:

Підставивши у третє рівняння, отримаємо:

Підставивши у друге рівняння, отримаємо:

Підставивши у перше рівняння, отримаємо:

Відповідь.

(Розв’язання контрольного завдання, виконаного студентом, може бути стислим і містити тільки необхідні алгебраїчні перетворення).

б)

Розв’язання.

Розглянемо розширену матрицю системи лінійних рівнянь:

Для зручності перетворень виберемо одиничний елемент із першого стовпця матриці: . Поміняємо місцями перший і другий рядок.

Перетворимо елементи матриці так, щоб усі елементи першого стовпця, крім елемента , стали нулями. Для цього всі елементи першого рядка:

помножимо на і додамо до відповідних елементів другого рядка;

помножимо на і додамо до відповідних елементів третього рядка;

помножимо на і додамо до відповідних елементів четвертого рядка.

Перетворимо елементи матриці так, щоб усі елементи другого стовпця «під елементом» стали нулями. Для цього всі елементи другого рядка матриці помножимо на і додамо до відповідних елементів третього рядка, а четвертий рядок помножимо на 4:

Другий рядок помножимо на і додамо до четвертого рядка:

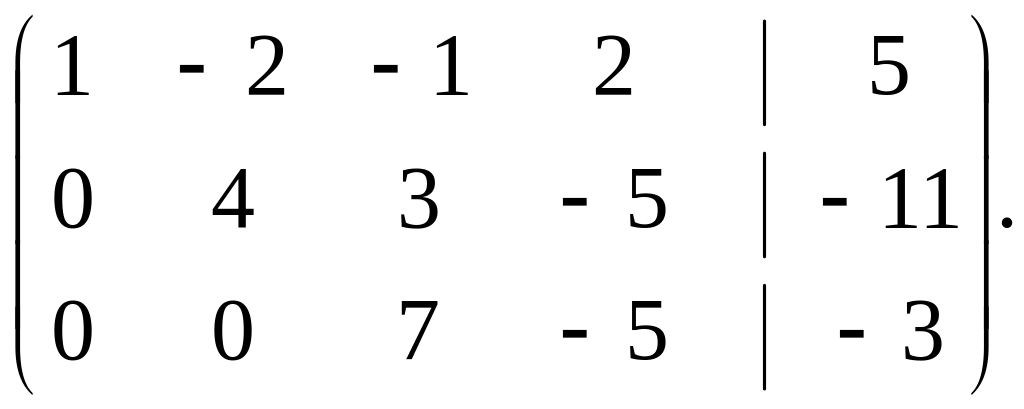
де число невідомих, тому за теоремою Кронекера-Капеллі система лінійних рівнянь є невизначеною (тобто має нескінченну множину розв’язків).

Запишемо систему лінійних рівнянь:

Нехай довільне дійсне число, тоді із третього рівняння системи визначимо:

Із другого рівняння системи виразимо

Із першого рівняння системи виразимо

Відповідь. Система лінійних рівнянь – невизначена.

довільне число.