§3. Системи лінійних алгебраїчних рівнянь.

Короткі теоретичні відомості.

Системою лінійних рівнянь із невідомими

називається система виду:

(6)

Числа називаються коефіцієнтами системи лінійних рівнянь, числа вільними членами.

Система лінійних рівнянь називається однорідною, якщо всі вільні члени і неоднорідною, якщо хоч один із вільних членів не дорівнює нулю.

Упорядкований набір чисел називається розв’язком системи лінійних рівнянь, якщо при підстановці цих чисел замість невідомих усі рівняння системи перетворюються в тотожності.

Система лінійних рівнянь називається сумісною, якщо вона має хоч один розв’язок, і несумісною, якщо вона не має жодного розв’язку.

Сумісна система лінійних рівнянь називається визначеною, якщо вона має єдиний розв’язок . Сумісна система лінійних рівнянь називається невизначеною, якщо вона має більше, ніж один розв’язок.

Розв’язування систем лінійних рівнянь за формулами Крамера

Нехай задано систему х лінійних рівнянь із трьома невідомими

Позначимо визначники:

1) Якщо то система лінійних рівнянь – визначена (має єдиний розв’язок) і

невідомі обчислюють за формулами Крамера:

(7)

2) Якщо і хоча б один із визначників не дорівнює нулю, то система лінійних рівнянь – несумісна (не має розв’язків).

3) Якщо то система лінійних рівнянь – невизначена (має нескінченну множину розв’язків).

Розв’язування систем лінійних рівнянь матричним методом

Нехай задано систему х лінійних рівнянь із трьома невідомими

Розглянемо матриці: тоді задану систему лінійних рівнянь можна записати за допомогою матричного рівняння: Розв’язком цього матричного рівняння є матриця-стовпець невідомих де обернена матриця до матриці

Обернену матрицю знаходять за формулою:

(8)

де алгебраїчні доповнення елементів визначника

Зразок виконання контрольного завдання №2.

За формулами Крамера та методом оберненої матриці розв'язати систему лінійних рівнянь:

Розв’язання.

1) Використаємо формули Крамера:

тому система лінійних рівнянь – визначена (має єдиний розв’язок).

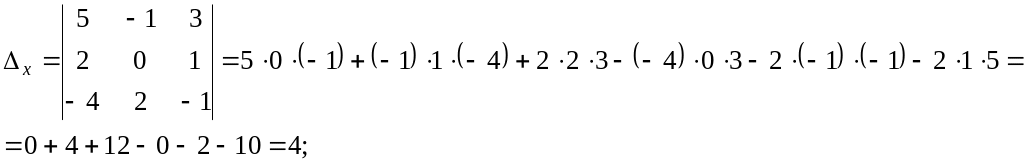
За формулами (7):

Відповідь.

2) Використаємо матричний метод.

Розглянемо матриці: тоді задану систему лінійних рівнянь можна записати за допомогою матричного рівняння розв’язок якого знайдемо із виразу де обернена матриця до матриці

Знайдемо матрицю обернену до матриці , за формулою (8):

тоді матриця невироджена і має обернену

Знайдемо алгебраїчні доповнення визначника

Відповідь.

Формули Крамера та матричний метод можуть застосовуватися тільки для розв’язування систем рівнянь, у яких кількість невідомих дорівнює кількості рівнянь . Крім цього, формули Крамера та матричний метод не дозволяють розв’язувати невизначені системи лінійних рівнянь.