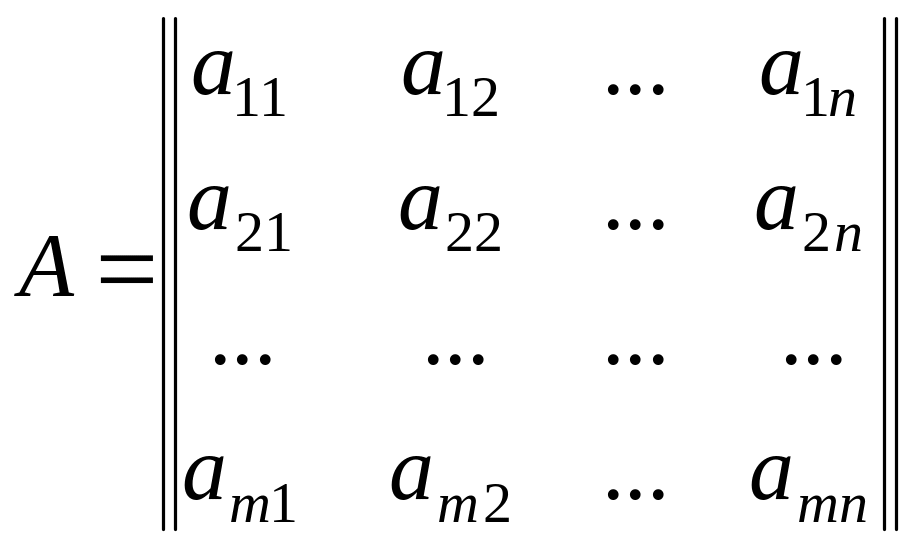ВИЩА МАТЕМАТИКА

Модуль 1. Елементи лінійної та векторної алгебри

Методичні вказівки для самостійної роботи

УКРАЇНА

Національний університет біоресурсів і природокористування України

Ніжинський агротехнічний інститут

Кафедра природничо-фундаментальних дисциплін

ВИЩА МАТЕМАТИКА

Модуль 1. Елементи лінійної та векторної алгебри

Методичні вказівки для самостійної роботи

Укладач: Муквич М.М.

Ніжин –2011

УДК 512 (073)

Рекомендовано до друку Вченою Радою

Ніжинського агротехнічного інституту

Національного університету біоресурсів і природокористування України

Протокол № 5 від 28 грудня 2011 р.

Укладач: М.М. Муквич, кандидат технічних наук.

Рецензенти:

В.М. Лось, к. ф.-м. наук, доцент, завідувач кафедри вищої та прикладної математики Чернігівського державного технологічного університету

Н.В. Майбородіна, к. ф.-м. наук, старший викладач кафедри природничо-фундаментальних дисциплін Ніжинського агротехнічного інституту

ВИЩА МАТЕМАТИКА. Модуль 1. Елементи лінійної та векторної алгебри: Методичні вказівки для самостійної роботи / Укл.: М.М. Муквич. – Ніжин: Видавець ПП Лисенко М.М, 2011.– 40 с.

Наведено короткі теоретичні відомості розділу «Елементи лінійної та векторної алгебри», індивідуальні контрольні завдання та зразки їх розв’язань.

Для самостійної роботи студентів інженерних напрямів підготовки.

© Укл. Муквич М.М., 2011

© ПП Лисенко М.М., 2011

ВСТУП

Методичні засади вивчення математики у загальноосвітній школі та у вищому навчальному закладі мають значні відмінності. При вивченні дисципліни «Вища математика», яка забезпечує основу для подальшої інженерної підготовки, оволодіння основами сучасного математичного апарату неможливе без організованої самостійної роботи студентів. Тому метою даного навчального видання є створення сприятливих умов для самостійного формування у першокурсників навичок до використання математичних методів при розв’язуванні прикладних задач.

У навчальному виданні розглянуто контрольні завдання згідно тем індивідуальних (розрахунково-графічних) завдань, наведених у програмах з навчальної дисципліни «Вища математика», для підготовки фахівців ОКР «бакалавр» напрямів підготовки:

6.100101 «Енергетика та електротехнічні системи в агропромисловому комплексі» у вищих навчальних закладах II – IV рівнів акредитації Міністерства аграрної політики України (автори Ю.Б. Гнучій, Н.Г. Батечко, О.Ю. Дюженкова, Р.Ф. Овчар, О.І. Завгородній. – Київ: Аграрна освіта, 2010);

6.100102 «Процеси, машини та обладнання агропромислового виробництва» у вищих навчальних закладах II – IV рівнів акредитації Міністерства аграрної політики України (автори Ю.Б. Гнучій, Н.Г. Батечко, О.Ю. Дюженкова, Р.Ф. Овчар, О.І. Завгородній, В.І. Кравець. – Київ: Аграрна освіта, 2010).

Для самостійного контролю при засвоєнні навчального матеріалу необхідно використовувати контрольні запитання, які подано в методичних вказівках.

Символ означає виконання прямого і оберненого твердження (скорочений запис необхідної і достатньої умови).

Початок і кінець наведеного розв’язку завдання позначено символами та відповідно.

Модуль 1. Елементи лінійної та векторної алгебри.

§1. Матриці. Дії над матрицями. Визначники та їх властивості.

Короткі теоретичні відомості.

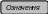Прямокутна таблиця чисел, записаних у вигляді:

або

(1)

і складена з m рядків та n стовпців називається матрицею розміру

Числа називаються елементами матриці.

Короткий запис матриці: або .

Матриця, в якої число рядків дорівнює числу стовпців, називається квадратною. Кількість рядків (або стовпців) квадратної матриці називається її порядком.

Дві матриці називаються рівними, якщо вони однакових розмірів і мають рівні відповідні елементи:

Квадратна матриця називається діагональною, якщо всі її елементи, крім головної діагоналі, дорівнюють 0. Діагональна матриця, у якої всі елементи головної діагоналі дорівнюють 1, називається одиничною і позначається E.

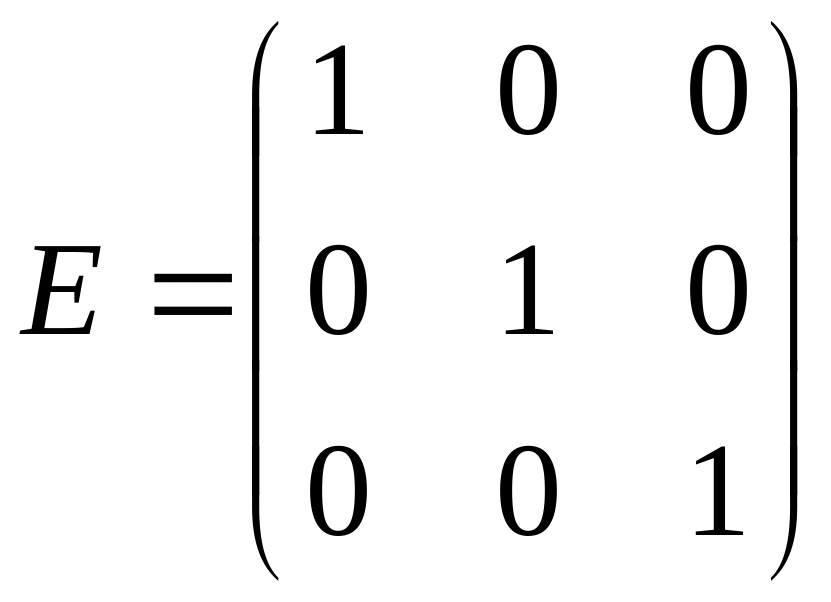– одинична матриця III – го порядку.

Серед дій над матрицями вирізняють додавання, віднімання, множення матриць, множення матриці на число.

Сумою двох матриць називається матриця

Додавати можна матриці тільки однакового розміру.

Добутком матриці на число називається матриця

Різницею двох матриць називається матриця

Віднімати можна матриці тільки однакового розміру.

Дано матриці А= і B= .

Знайти:

Розв’язання.

A+B= ;

;

.

Відповідь.

Множення двох матриць.

Матриця називається узгодженою з матрицею , якщо кількість стовпчиків n матриці дорівнює кількості рядків матриці :

узгоджені матриці.

Перемножити можна тільки узгоджені матриці.

Добутком

називається матриця , у якої елемент дорівнює сумі добутків елементів

го рядка матриці на відповідні елементи го стовпця матриці

(2)

Знайти матрицю якщо

Розв'язання.

Матриці – узгоджені, тому їх можна перемножити. Згідно формули (2):

Відповідь.

§2. Визначники та їх властивості.

Вираз

(3)

називається визначником (детермінантом) II – го порядку.

Вираз

(4)

називається визначником (детермінантом) III – го порядку.

При позначенні елемента визначника: i – номер рядка, j – номер стовпця, на перетині яких стоїть даний елемент визначника.

Елементи утворюють головну діагональ визначника, а елементи – побічну діагональ.

Обчислити визначники:

Будь – якій квадратній матриці можна поставити у відповідність число, яке називається визначником матриці А го порядку і позначається:

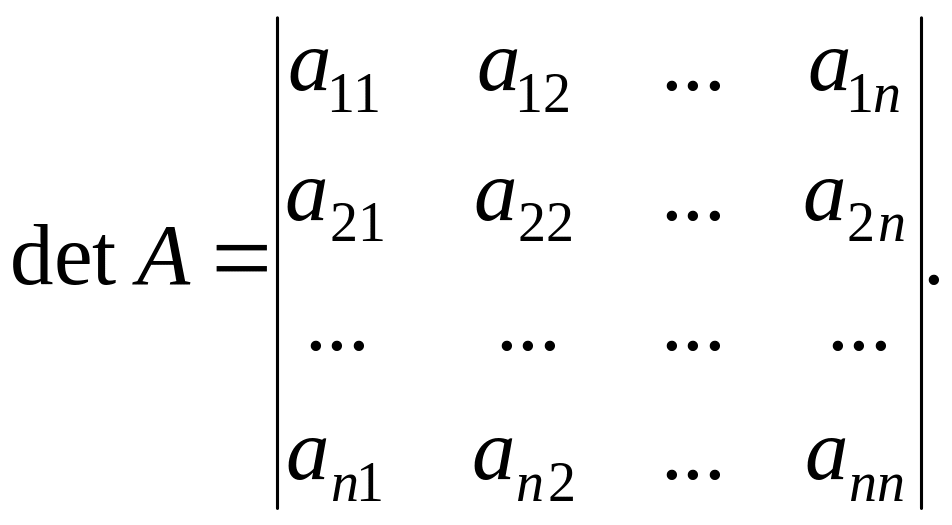
Основні властивості визначників.

1) Визначник дорівнює 0, якщо:

один із його рядків або стовпців складається тільки з нулів

або

визначник має два стовпчики (або рядки), відповідні елементи яких – рівні або пропорційні.

2) Значення визначника не зміниться, якщо його рядки замінити відповідними стовпцями:

3) Спільний множник, який міститься в усіх елементах одного рядка (або стовпця) визначника, можна винести за знак визначника.

4) Якщо переставити місцями два рядки (або стовпці), то визначник поміняє знак.

5) Значення визначника не зміниться, якщо до елементів одного рядка (або стовпця) додати відповідні елементи іншого рядка (або стовпця), помножені на одне й те саме число k .

Наприклад :

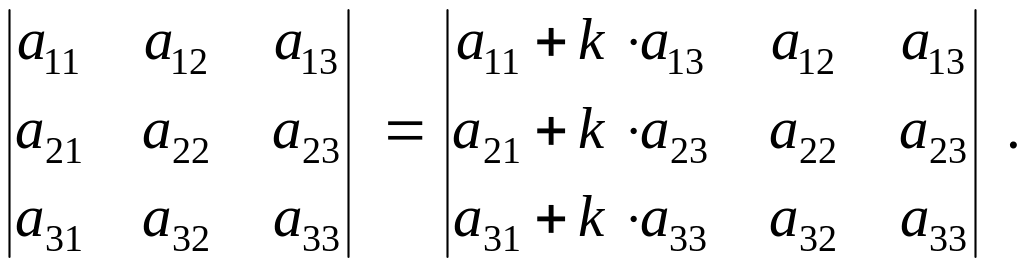
Мінором елемента визначника називається визначник, який утворюється з даного визначника викресленням i –го рядка і j –го стовпця.

Алгебраїчним доповненням елемента називається його мінор, взятий із знаком , тобто

(5)

Для визначника ,

мінор ;

згідно формули (5), алгебраїчне доповнення:

Визначник дорівнює сумі добутків елементів якого – небудь рядка (або стовпця) на їхні алгебраїчні доповнення.

Обчислити визначники:

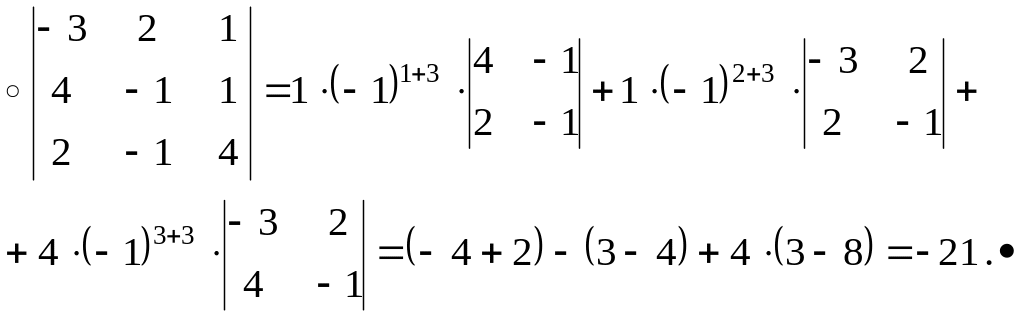
При обчисленні визначника го і вищих порядків необхідно перетворити його, користуючись властивістю (5), до вигляду, коли в якому– небудь рядку (або стовпці) визначника всі елементи, крім одного, будуть дорівнювати 0, і після цього застосувати теорему 1.

Зразок виконання контрольного завдання №1.

Знайти добуток матриць та визначник матриці , якщо

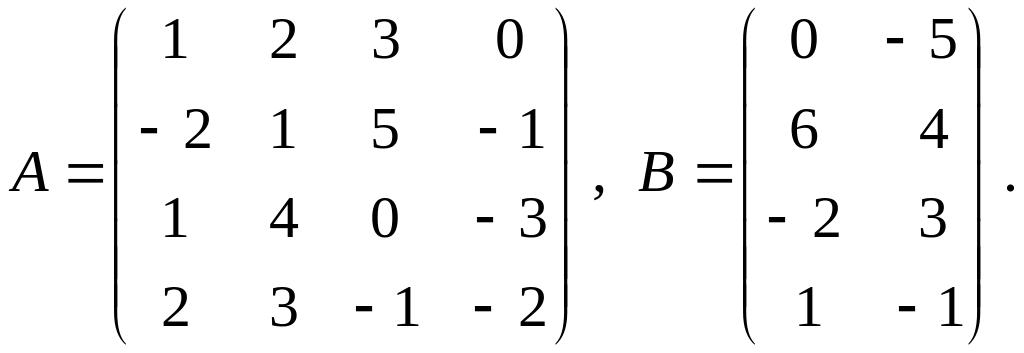
Розв'язання.

Матриці і узгоджені, тому їх можна перемножити.

Виберемо для зручності обчислення одиничний елемент визначника матриці :

Зведемо обчислення визначника матриці го порядку до визначника го порядку, перетворивши його елементи так, щоб усі елементи першого стовпця, крім елемента стали нулями. Для цього всі елементи першого рядка визначника:

помножимо на 2 і додамо до відповідних елементів другого рядка;

помножимо на –1 і додамо до відповідних елементів третього рядка;

помножимо на –2 і додамо до відповідних елементів четвертого рядка.

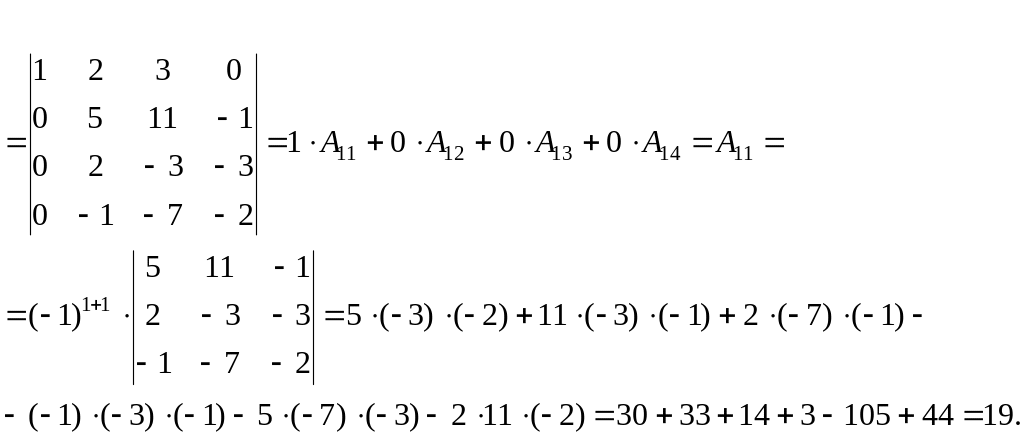
Відповідь.