III. Метод наименьших квадратов

В методе наименьших квадратов параметры уравнения y = f(x, a₁, . . ., a_k) определяются исходя из условия минимума суммы квадратов отклонений по всем точкам между расчетными и экспериментальными значениями:

. (7)

Поскольку критерий R(a₁,. . ., a_k) является функцией неизвестных параметров, его использование позволяет свести систему (7) к нормальному виду, т.е. виду, когда число неизвестных равно числу уравнений.

Условием существования экстремума функции нескольких переменных является равенство нулю частных производных по каждой из переменных. Поэтому для приведения системы (7) к виду, удобному для решения, необходимо найти частные производные функции R по каждой из переменных a₁, . . . , a_k:

. (8)

Так, например, для той же функции y_i^P=ax_i² + bx_i + c, система уравнений (8) будет выглядеть:

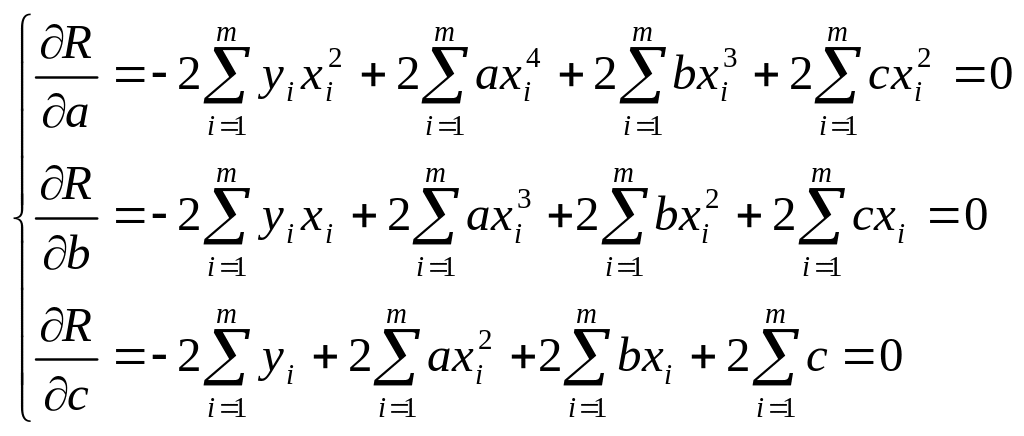(9)

или

. (10)

Коэффициенты зависимости (1) получают в результате решения системы уравнений (10).

Если функциональная зависимость является нелинейной относительно искомых параметров, то нахождение коэффициентов представляет собой определенные трудности. Это объясняется тем, что, во-первых, не всегда имеется возможность аналитического вычисления частных производных (8), во-вторых, полученная система уравнений будет не линейна относительно искомых коэффициентов и ее решение сопряжено с рядом вычислительных трудностей.

Например, y = ax^b - нелинейна относительно а,b однако после логарифмирования уравнения получим

y^/= a^/ + bx^/; где y^/ = ln y; x^/ = ln x; a^/ = ln a

Т.е. получена линейная зависимость у^/ = f(x^/, a^/, b). В этом случае при определении коэффициентов a^/, b можно воспользоваться методами решения системы линейных уравнений.

4. Контрольные вопросы и задания

1. Сформулировать задачу аппроксимации.

2. Объяснить отличие и сходство задач аппроксимации и интерполирования.

3. Привести примеры области применения задач аппроксимации и интерполирования.

4. Сформулировать условие аппроксимации?

5. Привести нелинейную математическую модель к линейному виду.

6. Осуществить аппроксимацию методом выбранных точек.

7. Осуществить аппроксимацию методом средних.

8. Осуществить аппроксимацию методом наименьших квадратов.

6. Требования к отчету

Отчет о работе должен содержать название работы, цель, постановку задачи, исходные данные, математическую формулировку, схему алгоритма, листинг программы, распечатку результатов, анализ полученных результатов.

ПРИЛОЖЕНИЕ 1

Варианты 1.1 – 1.3

Вязкость пластичной жидкости находится по следующей формуле:

,

где - напряжение внутреннего трения при котором пластичная жидкость начинает движение, Н/м²; d – диаметр проходного сечения; - средняя скорость жидкости, м/c; - коэффициент пропорциональности, характеризующий пластичные свойства жидкости.

Определить и , если известно, что d=0.2 м и в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	I	1	2	3	4	5	6	7	8
1.1		0.2	0.25	0.4	0.6	0.7	0.75	0.9	-	Крамера
		992	840	640	460	390	380	350	-
1.2		0.3	0.4	0.7	0.9	1.2	1.4	1.5	1.7	Гаусса
		175	158	140	138	134	130	128	130
1.3		0.25	0.5	0.6	1	1.5	2	2.75	4	Обращения матриц
		7200	3533	2800	1900	1200	900	700	500

Варианты 1.4 – 1.6

Эффективную скорость газа, соответствующую началу подвисания жидкости при прохождении газа через нее можно найти по числу Рейнольдса, определяемого по формуле:

,

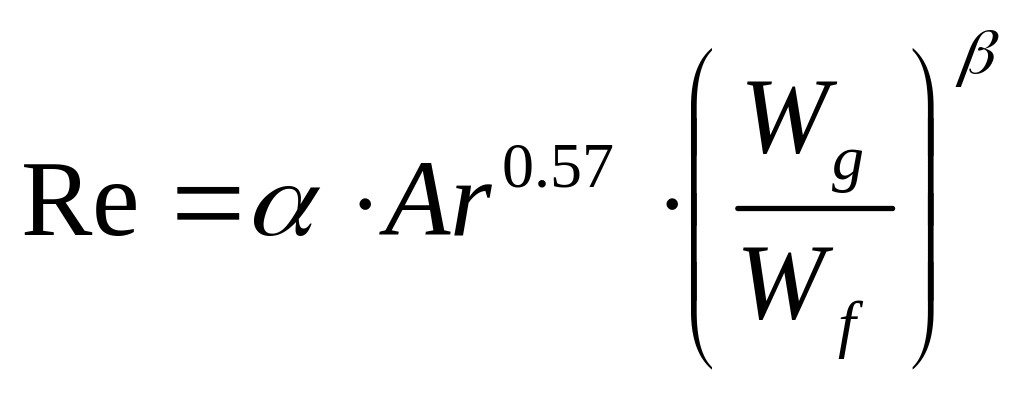где - критерий Архимеда, соответствующему эквивалентному диаметру насадки и плотности газа; и - скорости газа и жидкости, кг/ч; и - константы.

Определить и , если известно, что =12300 кг/ч, =46 и в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	I	1	2	3	4	5	6	7	8
1.4	Wf	5	10	20	25	30	50	60	80	Обращения матриц
	Re	1700	1000	800	700	700	500	460	400
1.5	Wf	2	5	10	30	60	90	100	-	Гаусса
	Re	3500	1900	1000	500	300	200	200	-
1.6	Wf	2	7	15	40	70	80	-	-	Крамера
	Re	9900	1700	50	10	15	10	-	-

Варианты 1.7 – 1.9

Постоянная составляющая помехи в электрической сети описывается следующей математической моделью:

где и - угловые скорости, рад/с; t – время, с; - напряжение, В; , , - константы.

Определить , , , если известно, что =5 рад/с, =10 рад/с и в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	I	1	2	3	4	5	6	7	8
1.7		0.1	0.5	0.6	0.8	1.1	1.4	1.6	1.8	Обращения матриц
	U	25	18	-16	-5	10	22	-2	-20
1.8		0.2	0.3	0.5	0.8	0.9	1	1.2	1.4	Гаусса
	U	50	32	4	27	30	30	43	60
1.9		0.1	0.2	0.4	0.8	0.9	1	1.2	1.5	Крамера
	U	3.2	3.3	2.7	3.1	3.05	2.9	3	3.2

Варианты 1.10 -1.13

Изменение температуры в зависимости о времени в трубчатом реакторе можно описать следующей математической моделью:

,

где t – время, с; Т- температура реакционной массы, К; , , - константы.

Определить , , , если известно, что в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	i	1	2	3	4	5	6	7	8
1.10	t	10	40	50	70	80	90	100	-	Крамера
	T	292	300	302	305	310	315	320
1.11	t	5	10	30	40	60	80	90	100	Обращения матриц
	T	300	301	300.5	300.5	299	295	293	290
1.12	t	1	5	10	15	20	40	80	100	Гаусса
	T	330	335	348	352	360	370	385	390
1.13	t	1	5	10	15	20	40	-	-	Обращения матриц
	T	300	297	297	300	301	305	-	-

Варианты 2.1 -2.3

Константа скорости химической реакции подчиняется закону Аррениуса:

,

где - постоянная скорости химической реакции,; Т - температура реакционной массы, К; E – энергия активации, кДж/моль; R = 8.32 универсальная газовая постоянная, кДж/(Кмоль).

Определить и E, если известно, что в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	i	1	2	3	4	5	6	7	8
2.1	T	277.5	282	285	290	292	295	297.5	-	Обращения матриц
	K	1238	1239	1239.5	1240	1239.8	1240.5	1241	-
2.2	T	267	270	275	280	290	292.5	297	300	Гаусса
	K	960	963	967	967	972	972	975	976
2.3	T	250	255	262	270	277	287	295	-	Крамера
	K	4250	4166	4189	4205	4232	4255	4280	-

Варианты 2.4 -2.9

Зависимость максимальной ньютоновской вязкости полимера в растворе без учета средневязкостного молекулярного веса и коэффициента полидисперсности полимера выглядит следующим образом:

,

где Т- температура реакционной массы, К; R = 8.32 универсальная газовая постоянная, кДж/(Кмоль); - концентрация полимера, безразм.; a1, a2, a3, – константы; А – поправочный коэффициент ед. измерения, Пас.

а) Определить значения констант a1, a2, a3 при Т= 300 К, А = 0.51 Пас, если известны следующие экспериментальные данные

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	I	1	2	3	4	5	6	7	8
2.4		0.05	0.2	0.4	0.6	0.8	0.9	0.95	-	Гаусса
		0.1	0.3	0.6	0.9	1.2	1.5	1.5	-
2.5		0.1	0.2	0.3	0.4	0.7	0.8	0.9	-	Крамера
		2	3.5	5.1	6	8.5	9	9.4	-
2.6		0.05	0.15	0.3	0.4	0.5	0.6	0.7	0.9	Обращения матриц
		4	9	16	18	22	25	27	31

б) Определить значения констант А и a3 при C_p= 0.5, a1=1.9, a2=2.7, если известны следующие экспериментальные данные

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	I	1	2	3	4	5	6	7	8
2.7	Т	260	275	280	285	290	310	320	340	Крамера
		7	5	4	3.5	3	2	1.8	1
2.8	Т	255	270	290	300	320	330	350	-	Обращения матриц
		14	12	9	9	7	7	5	-
2.9	Т	280	285	305	320	330	340	350	-	Гаусса
		17	17	15	14	14	14	13.5	-

Варианты 2.10 – 2.13

Постоянная составляющая помехи в электрической сети описывается следующей математической моделью:

,

где - угловая скорость, рад/с; t – время, с; - напряжение, В; , , - константы.

Определить , , , если известно, что =15 рад/с и в ходе исследования получены следующие экспериментальные данные:

Номер варианта	Экспериментальные данные									Метод решения системы линейных уравнений
	I	1	2	3	4	5	6	7	8
2.10		0.05	0.15	0.2	0.3	0.7	0.8	0.85	0.9	Крамера
	U	12	15	7	-5	0	5	15	25
2.11		0.1	0.15	0.2	0.3	0.4	0.5	0.55	-	Гаусса
	U	12	12	10	5	14	25	27	-
2.12		0.05	0.1	0.25	0.4	0.6	0.65	0.8	-	Крамера
	U	-7	-3	2	10	22	22	32	-
2.13		0	0.2	0.3	0.4	0.5	0.6	0.7	1	Обращения матриц
	U	30	24	24	18	14	12	12	0