Ф едеральное агентство по образованию
В ОРОНЕЖСКАЯ ГОСУДАРСТВЕННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ
К
АФЕДРА
ИНФОРМАЦИОННЫХ И УПРАВЛЯЮЩИХ СИСТЕМ
ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МЕТОДАМИ
АППРОКСИМАЦИИ
Методические указания для выполнения
контрольной работы №1 по дисциплине
“Численные методы”
Для бакалавров, обучающихся по направлениям
220400 ‑ «Управление и информатика в технических системах»
и 220700 – «Автоматизация технологических процессов
и производств»
заочной формы обучения
ВОРОНЕЖ
2006
УДК 519.852.6
Параметрическая идентификация математических моделей методами аппроксимации: Методические указания для выполнения контрольной работы по дисциплине “Численные методы”/ Воронеж. гос. технол. акад.; Сост. С.Г. Тихомиров, И.А. Хаустов, А.А. Хвостов. Воронеж, 2006. 16 с.
Указания разработаны в соответствии с ФГОС ВПО подготовки бакалавров по направлениям 220700 ‑«Автоматизация технологических процессов и производств» и 220400 ‑«Управление и информатика в технических системах». Методические указания посвящены обучению навыкам параметрической идентификации линейных и нелинейных математических моделей с использованием методов аппроксимации: метода выбранных точек, метода средних и метода наименьших квадратов - с разработкой программ в среде СИ++.
Ил. 1. Библиогр.: 4 назв.
Составители доцент С.Г. ТИХОМИРОВ,
ст. преподаватели И.А. ХАУСТОВ, А.А. ХВОСТОВ
Научный редактор профессор, д.т.н. В.Ф. ЛЕБЕДЕВ
Рецензент профессор, д.т.н. Ю.А. ЧЕВЫЧЕЛОВ
Печатается по разрешению
редакционно-издательского совета
Воронежской государственной технологической академии
Тихомиров С.Г.,
Хаустов И.А.,
Хвостов А.А., 2006
Воронежская
государственная
технологическая
академия, 2006
Цель работы:
Освоение методов аппроксимации: метода выбранных точек, метода средних и метода наименьших квадратов (МНК).
Осуществление параметрической идентификации математической модели с использованием указанных методов и оценка точности аппроксимации.
Постановка задачи
1. В соответствии с выбранным вариантом осуществить параметрическую идентификацию математической модели по имеющимся экспериментальным данным (приложение 1) тремя методами аппроксимации: методом выбранных точек, методом средних и методом наименьших квадратов.
Оценить погрешность методов аппроксимации по следующей формуле:
,
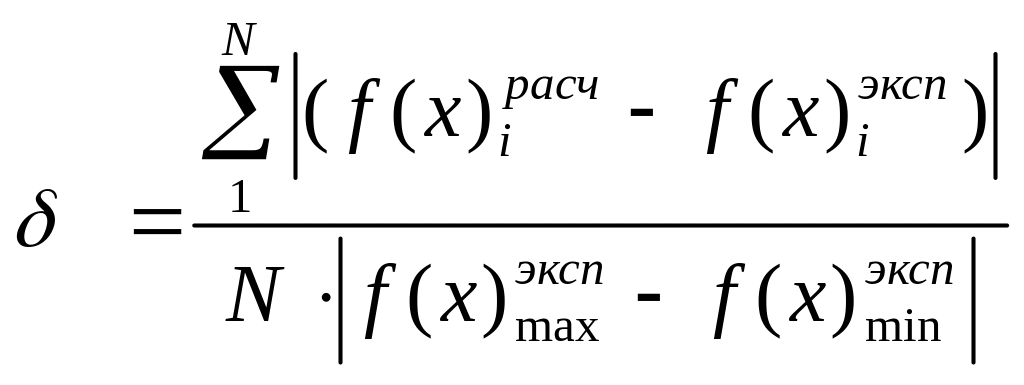где
N-
число экспериментальных точек;
и
- экспериментальные
и рассчитанные по выбранному методу
значения;
и
- максимальные и
минимальные экспериментальные значения.
Составить алгоритм и программу расчета неизвестных параметров математической модели, обеспечив универсальность программы, т.е. предусмотреть аппроксимацию m экспериментальных точек.
Дать сравнительную характеристику используемых методов аппроксимации:
сложность реализации метода (указать преимущества и недостатки).
точность метода.
Результаты получить в табличном виде:
i
Экспериментальные значения
Расчетные значения
x
f(x)
f(x) по методу выбранных точек
f(x) по методу средних
f(x) по методу наименьших квадратов
1
N
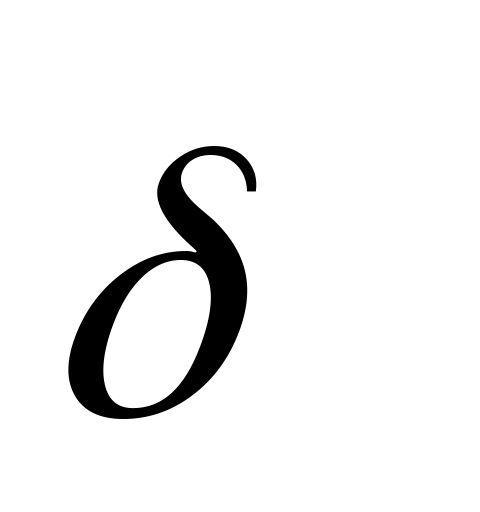
Оформить отчет.