
- •Гармонические колебания
- •[Править]Нелинейный маятник
- •Определения
- •Дифференциальное уравнение движения физического маятника
- •Период колебаний физического маятника
- •Векторная диаграмма и применение её при сложении гармонических колебаний одного направления и одинаковой частоты. Биения.
- •Сложения взаимно перпендикулярных колебаний. Фигуры Лиссажу.
- •Свободные затухающие механические колебания, их дифференциальное уравнение и его решение.
- •Свободные затухающие колебания в электрическом колебательном контуре, их дифференциальное уравнение и его решение.
- •Вынужденные механические колебания, их амплитуда и фаза. Случай резонанса.
- •Вынужденные электромагнитные колебания.
- •Переменный ток в цепях, содержащих резистор, катушку индуктивности и конденсатор. Резистор, конденсатор и катушка индуктивности в цепи переменного тока.
- •Волны в упругой среде. Продольные и поперечные волны. Скорость волны. Длина волны и волновое число. Уравнение бегущей волны.
- •Энергия волны. Поток энергии, его плотность. Вектор Умова. Энергия волны
- •Образование стоячих волн. Уравнение стоячей волны.
- •Звуковые волны и их характеристики. Ультразвук и его применение.
- •Применение ультразвука [править]Диагностическое применение ультразвука в медицине (узи)
- •[Править]Терапевтическое применение ультразвука в медицине
- •[Править]Резка металла с помощью ультразвука
- •[Править]Приготовление смесей с помощью ультразвука
- •[Править]Применение ультразвука в биологии
- •[Править]Применение ультразвука для очистки
- •[Править]Применение ультразвука в гальванотехнике
- •Когерентность и монохроматичность световых волн. Интерференция света. Условия интерференционных максимумов и минимумов.
- •§1 Когерентность и монохроматичность световых волн
- •§2 Интерференция света в тонких плоскопараллельных
- •Условие максимума и минимума интерференции
- •Метод получения когерентных световых волн. Расчет интерференционной картины от двух источников.
- •Интерференция света в тонких пленках.
- •Интерференция света в тонких плёнках
- •Кольцо Ньютона. Применение интерференции света (просветление оптики, интерферометра).
- •Дифракция света. Принцип Гюйгеса-Френеля. Метод зон Френеля.
- •Дифракция Френеля на круглом отверстии и диске. Дифракция Фраунгофера на одной щели.
- •Дифракционная решетка и её применение. Дифракционный спектр. Исследование структуры кристаллов.
- •Применение
- •Дифракция на пространственной решетке. Формула Вульфа-Брэгга. Исследование структуры кристаллов.
- •Дисперсия света. Области нормальной и аномальной дисперсии. Применение дисперсии света. Дисперсионный спектр.
- •Дисперсионный спектр
- •Поглощение света. Закон Бугера. Рассеяние света. Закон Рэлея.
- •Закон Бугера — Ламберта — Бера
- •Закон рэлея и его объяснение
- •Естественный и поляризованный свет. Поляризация света при отражении и преломлении. Закон Брюстера.
- •Поляризация света при отражении и преломлении на границе двух диэлектриков
- •Двойное лучепреломление. Поляризованные призмы и поляроиды. Закон Малюса. Двойное лучепреломление
- •§ 193. Поляризационные призмы и поляроиды
- •Закон Малюса
- •Искусственная оптическая анизотропия. Эффект Керра. Вращение плоскости поляризации. Искусственная оптическая анизотропия
- •§ 196. Вращение плоскости поляризации
- •Тепловое излучение и его характеристики. Абсолютно черное тело. Закон Кирхгофа.
- •Закон Стефана-Больцмана. Закон смещения Вина. Второй закон Вина.
- •Распределение энергии в спектре абсолютно черного тела. Формула Рэлея-Джинса. Ультрафиолетовая катастрофа. Квантовая гипотеза и формула Планка.
- •Внешний фотоэффект и его законы. Фотоны. Уравнение Эйнштейна для внешнего фотоэффекта. Фотоэлементы и их применение.
- •Фотоэлементы промышленного назначения
- •Внешний фотоэффект
- •[Править]Законы внешнего фотоэффекта
- •Давление света. Опыт Лебедева. Волновое и квантовое объяснение давления света. Давление света. Опыты п.Н.Лебедева
- •Эффект Комптона и его элементарная теория.
- •Энергия и импульс фотона. Диалектическое единство корпускулярных и волновых свойств электромагнитного излучения.
- •Фотоны, энергия, масса и импульс фотона
- •Формула де Бройля. Корпускулярно-волновой дуализм свойств вещества и его опытное обоснование. Волны де Бройля
- •Соотношение неопределенностей. Соотношения неопределённостей Uncertainty relations
- •Волновая функция и её статистический смысл.
- •Общее уравнение Шредингера. Уравнение для стационарных состояний. Принцип причинности в квантовой механике.
- •Формулировка [править]Общий случай
- •Частица в одномерной прямоугольной «потенциальной яме». Принцип соответствия Бора. Понятие о туннельном эффекте.
- •Упрощённое объяснение
- •Принцип соответствия в квантовой механике
- •Опыт Резерфорда по рассеянию альфа-частиц веществом. Ядерная модель атома.
- •Опыты по рассеянию альфа-частиц
- •Неустойчивость атома Резерфорда (Ядерная модель атома)
- •Постулаты Бора. Опыт Франка и Герца.
- •Теория атома водорода по Бору. Затруднение теории Бора. Боровская модель атома
- •Достоинства теории Бора
- •[Править]Недостатки теории Бора
- •Атом водорода в квантовой механике. Главное, орбитальное и магнитное квантовые числа.
- •Спин электрона. Магнитное спиновое квантовое число.
- •Принцип Паули. Распределение электронов в атоме по состояниям.
- •Молекулярные спектры. Комбинационное рассеяние света.
- •Поглощение, спонтанное и вынужденное излучение. Оптические квантовые генераторы (лазеры).
- •§7. Лазеры - оптические квантовые генераторы
- •Понятие о зонной теории твердых тел. Собственная и примесная проводимость полупроводников. Фотопроводимость.
- •Люминесценция твердых тел.
- •Размер, состав и заряд атомного ядра. Массовое и зарядовое числа.
- •Ядерные силы, их основные свойства. Модели ядра.
- •Дефект массы и энергия связи атомного ядра.
- •Радиоактивное излучение и его виды. Закон радиоактивного распада. Правила смещения. Активность источника радиоактивного излучений.
- •Метод наблюдения и регистрации радиоактивных излучений и частиц.
- •Ядерные реакции и их основные типы. Реакция деления. Цепная реакция деления тяжелых ядер. Реакция синтеза атомных ядер.
Гармонические колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний.
Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
![]()
или
![]() ,
,
где х —
смещение (отклонение) колеблющейся
точки от положения равновесия в момент
времени t; А —
амплитуда колебаний, это величина,
определяющая максимальное отклонение
колеблющейся точки от положения
равновесия; ω —
циклическая частота, величина, показывающая
число полных колебаний происходящих в
течение 2π секунд ![]() —
полная фаза колебаний,
—
полная фаза колебаний, ![]() —
начальная фаза колебаний.
—
начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
![]()
Колебания называются свободными (или собственными),
если они совершаются за счет первоначально
сообщенной энергии при последующем
отсутствии внешних воздействий на
систему, которая совершает колебания.
Простейшим типом колебаний
являютсягармонические
колебания —
колебания, при которых колеблющаяся
величина изменяется со временем по
закону синуса (косинуса). Исследование
гармонических колебаний важно по двум
причинам: 1) колебания, которые встречаются
в природе и технике, часто имеют близкий
к гармоническому характер ; 2)
различные периодические
процессы (процессы,
которые повторяются через равные
промежутки времени) можно представить
как суперпозицию (наложение) гармонических
колебаний. Гармонические колебания
некоторой величины s описываются
уравнением вида
![]() (1)
где
ω0 — круговая
(циклическая) частота,
А - максимальное значение колеблющейся
величины, называемое амплитудой
колебания,
φ — начальная
фаза колебания в
момент времени t=0, (ω0t+φ)
- фаза
колебания в
момент времени t. Фаза колебания есть
значение колеблющейся величины в данный
момент времени. Так как косинус имеет
значение в пределах от +1 до –1, то s может
принимать значения от +А до –А.
Определенные
состояния системы, которая совершает
гармонические колебания, повторяются
через промежуток времени Т, имеющий
название период
колебания,
за который фаза колебания получает
приращение (изменение) 2π, т.
е.
(1)
где
ω0 — круговая
(циклическая) частота,
А - максимальное значение колеблющейся
величины, называемое амплитудой
колебания,
φ — начальная
фаза колебания в
момент времени t=0, (ω0t+φ)
- фаза
колебания в
момент времени t. Фаза колебания есть
значение колеблющейся величины в данный
момент времени. Так как косинус имеет
значение в пределах от +1 до –1, то s может
принимать значения от +А до –А.
Определенные
состояния системы, которая совершает
гармонические колебания, повторяются
через промежуток времени Т, имеющий
название период
колебания,
за который фаза колебания получает
приращение (изменение) 2π, т.
е.
![]() откуда
откуда
![]() (2)
Величина,
обратная периоду колебаний,
(2)
Величина,
обратная периоду колебаний,
![]() (3)
т.
е. число полных колебаний, которые
совершаются в единицу времени,
называется частотой
колебаний.
Сопоставляя (2) и (3), найдем
(3)
т.
е. число полных колебаний, которые
совершаются в единицу времени,
называется частотой
колебаний.
Сопоставляя (2) и (3), найдем
![]() Единица
частоты — герц (Гц):
1 Гц — частота периодического процесса,
во время которого за 1 с совершается
один цикл процесса.
Найдем
первую и вторую производные по времени
от величины s, совершающей гармонические
колебания:
Единица
частоты — герц (Гц):
1 Гц — частота периодического процесса,
во время которого за 1 с совершается
один цикл процесса.
Найдем
первую и вторую производные по времени
от величины s, совершающей гармонические
колебания:
![]() (4)
(4)
![]() (5)
т.
е. имеем гармонические колебания с той
же циклической частотой. Амплитуды
величин в формулах (4) и (5) соответственно
равны Аω0 и
Аω02 .
Фаза величины в формуле (4) отличается
от фазы величины в формуле (1) на π/2, а
фаза величины в выражении (5) отличается
от фазы величины (1) на π. Значит, в моменты
времени, когда s=0, ds/dt имеет наибольшие
значения; когда же s становится равным
максимальному отрицательному значению,
то d2s/dt2 равен
наибольшему положительному значению
(рис. 1).
(5)
т.
е. имеем гармонические колебания с той
же циклической частотой. Амплитуды
величин в формулах (4) и (5) соответственно
равны Аω0 и
Аω02 .
Фаза величины в формуле (4) отличается
от фазы величины в формуле (1) на π/2, а
фаза величины в выражении (5) отличается
от фазы величины (1) на π. Значит, в моменты
времени, когда s=0, ds/dt имеет наибольшие
значения; когда же s становится равным
максимальному отрицательному значению,
то d2s/dt2 равен
наибольшему положительному значению
(рис. 1).
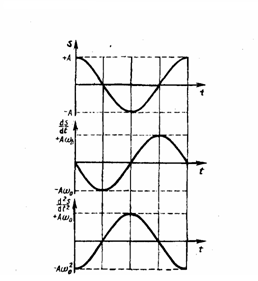
Рис.1
Из
выражения (5) непосредственно
вытекает дифференциальное
уравнение гармонических
колебаний
![]() (6)
(где
s = A cos(ω0t+φ)).
Решением данного дифференциального
уравнения является выражение
(1).
Гармонические
колебания графически изображаются методом
вращающегося вектора амплитуды,
или методом
векторных диаграмм.
Для этого из произвольной точки О,
которая выбрана на оси х, под углом φ,
который равен начальной фазе колебания,
откладывается вектор А, у которого
модуль равен амплитуде А рассматриваемого
колебания (рис. 2). Если данный вектор
привести во вращение с угловой скоростью
ω0,
которая равна циклической частоте
колебаний, то проекция конца вектора
будет перемещаться по оси х и принимать
значения от –А до +А, а колеблющаяся
величина будет изменяться со временем
по закону s = Acos(ω0t+φ).
Значит, гармоническое колебание можно
представить как проекцию на некоторую
выбранную произвольным образом ось
вектора амплитуды А, который отложен
из произвольной точки оси под углом φ
, равным начальной фазе, и вращающегося
с угловой скоростью ω0 вокруг
этой точки.
(6)
(где
s = A cos(ω0t+φ)).
Решением данного дифференциального
уравнения является выражение
(1).
Гармонические
колебания графически изображаются методом
вращающегося вектора амплитуды,
или методом
векторных диаграмм.
Для этого из произвольной точки О,
которая выбрана на оси х, под углом φ,
который равен начальной фазе колебания,
откладывается вектор А, у которого
модуль равен амплитуде А рассматриваемого
колебания (рис. 2). Если данный вектор
привести во вращение с угловой скоростью
ω0,
которая равна циклической частоте
колебаний, то проекция конца вектора
будет перемещаться по оси х и принимать
значения от –А до +А, а колеблющаяся
величина будет изменяться со временем
по закону s = Acos(ω0t+φ).
Значит, гармоническое колебание можно
представить как проекцию на некоторую
выбранную произвольным образом ось
вектора амплитуды А, который отложен
из произвольной точки оси под углом φ
, равным начальной фазе, и вращающегося
с угловой скоростью ω0 вокруг
этой точки.
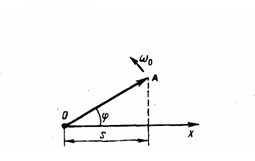
Рис.2
В
физике часто используется другой метод,
отличающийся от метода вращающегося
вектора амплитуды лишь по форме. В данном
методе колеблющуюся величину
представляют комплексным
числом.
Используя формулу Эйлера, для комплексных
чисел
![]() (7)
где
(7)
где ![]() -
мнимая единица. Значит уравнение
гармонического колебания (1) можно
представить в комплексной
форме:
-
мнимая единица. Значит уравнение
гармонического колебания (1) можно
представить в комплексной
форме:
![]() (8)
Вещественная
часть формулы (8)
(8)
Вещественная
часть формулы (8)
![]() есть
гармоническое колебание. Обозначение
Re вещественной части условимся опускать
и (8) записывать в форме
есть
гармоническое колебание. Обозначение
Re вещественной части условимся опускать
и (8) записывать в форме
![]() В
теории колебаний уславливаются, что
колеблющаяся величина s равна вещественной
части комплексного выражения, стоящего
в этом равенстве справа.
В
теории колебаний уславливаются, что
колеблющаяся величина s равна вещественной
части комплексного выражения, стоящего
в этом равенстве справа.
Свободные механические гармонические колебания. Координата, скорость и ускорение колеблющейся материальной точки.
Механические колебания – это повторяющееся движение, при котором тело
многократно проходит одно и то же положение в пространстве. Различают
периодические и непериодические колебания. Периодическими называют
колебания, при которых координата и другие характеристики тела описываются
периодическими функциями времени.
Примерами механических колебаний могут служить движение шара на пружине,
на нити, движение ножек звучащего камертона или молекул воздуха вблизи
него (рис. 1). В физике рассматривают и другие колебания – процессы, обладающие
той или иной степенью повторяемости во времени (например, электромагнитные
колебания.)
Колебания можно классифицировать по условиям возникновения (свободные,
вынужденные, автоколебания) и по характеру изменения во времени кинематических
характеристик (пилообразные, гармонические, затухающие).
Классификация колебаний :
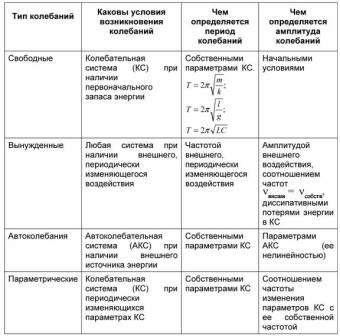
Для описания кинематических характеристик используют аналитическую
зависимость характеристики, например координаты или скорости от
времени u и графическое представление этой функции (рис. 2, а сложной формы,
б прямоугольные, в пилообразные, г гармонические, д затухающие, е нарастающие). – – – – – –(t),
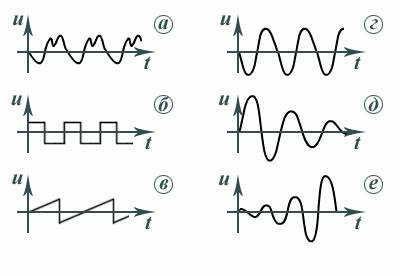
Рис. 2
Наиболее общими характеристиками колебаний являются следующие физические
величины: амплитуда колебаний А наибольшее отклонение колеблющегося
тела от положения равновесия (отклонение величины от ее среднего значения);
период колебаний Т время, через которое движение тела полностью
повторяется (повторяются все кинематические характеристики колебаний),
т.е. совершается одно полное колебание; частота колебаний v – величина,
показывающая число колебаний, совершаемых за 1 с. Вместо частоты v чаще
пользуются понятием циклической частоты w. Циклическая частота w – это
число колебаний, совершаемых за 2p секунд. Частота обратно пропорциональна
периоду: – –
![]() и
и ![]()
В СИ период Т выражается в секундах (c), частота v в герцах (Гц), циклическая
частота w – в обратных секундах (с–1). –
Единица амплитуды колебаний зависит от того, какая колеблющаяся физическая
величина рассматривается.
Для сравнения колебаний, происходящих с одной частотой, но различающихся по
тому, какую стадию полного колебания проходит тело, вводят понятие фазы
колебаний. Если два шарика на нитях одинаковой длины отвести от положения
равновесия вправо и отпустить, то они будут колебаться в фазе (синфазно,
синхронно), если их развести в разные стороны, то колебания будут происходить
в противофазе.
При описании колебаний с помощью функции изменения кинематической величины
во времени фазой j называют аргумент функции, описывающей колебательный
процесс.
Координата, скорость и ускорение колеблющейся материальной точки. Ответ ищи в 1-м вопросе
Кинетическая, потенциальная и полная энергия колеблющейся материальной точки.
При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:
![]()
(Скорость тела v = ds/dt)
Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:
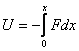
где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.
Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:
![]()
![]()
![]()
![]()
|
для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы: |
1.
Полная механическая энергия тела не
изменяется при колебаниях: ![]() 2.
Частота колебаний кинетической и
потенциальной энергии в 2 раза больше
частоты колебаний маятника.
3.
Колебания кинетической и потенциальной
энергии сдвинуты друг относительно
друга по фазе на (на
полпериода). Когда кинетическая энергия
достигает максимума, потенциальная -
минимума (нуля) и наоборот. Энергия при
колебаниях постоянно перекачивается
из потенциальной в кинетическую и
обратно.
2.
Частота колебаний кинетической и
потенциальной энергии в 2 раза больше
частоты колебаний маятника.
3.
Колебания кинетической и потенциальной
энергии сдвинуты друг относительно
друга по фазе на (на
полпериода). Когда кинетическая энергия
достигает максимума, потенциальная -
минимума (нуля) и наоборот. Энергия при
колебаниях постоянно перекачивается
из потенциальной в кинетическую и
обратно.
Пружинный маятник, дифференциальное уравнение его движения и период колебаний
Пружинный маятник – это тело массой m, подвешенное на абсолютно упругой пружине и совершающее гармонические колебания под действием упругой силы. Собственная частота колебаний такого маятника может быть найдена как wo = (k/m)1/2, где k – жесткость пружины.
Свободные
затухающие колебания пружинного
маятника.
Для пружинного маятника массой m, который
совершает малые колебания под действием
упругой силы F= -kx, сила трения прямо
пропорциональна скорости, т. е.
![]() где
r — коэффициент
сопротивления;
знак минус говорит о том, что сила трения
и скорость противоположно направлены.
При
этих условиях закон движения
маятника
где
r — коэффициент
сопротивления;
знак минус говорит о том, что сила трения
и скорость противоположно направлены.
При
этих условиях закон движения
маятника
![]() (9)
Используя
формулу
(9)
Используя
формулу ![]() и
считая, что коэффициент затухания
равен
и
считая, что коэффициент затухания
равен
![]() (10)
получим
полностью идентичное уравнению (1)
дифференциальное уравнение затухающих
колебаний маятника:
(10)
получим
полностью идентичное уравнению (1)
дифференциальное уравнение затухающих
колебаний маятника:
![]() Из
выражений (1) и (5) следует, что колебания
маятника удовлетворяют уравнению
Из
выражений (1) и (5) следует, что колебания
маятника удовлетворяют уравнению
![]() где
частота
где
частота ![]() (см.
(4)).
Добротность
пружинного маятника, используя (8) и
(10),
(см.
(4)).
Добротность
пружинного маятника, используя (8) и
(10), ![]() .
.
.
Математический маятник, дифференциальное уравнение его движения и период колебаний.
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения[1]. Период малых собственных колебанийматематического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
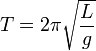
и не зависит[2] от амплитуды колебаний и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
![]()
где ![]() — амплитуда колебаний
маятника,
— амплитуда колебаний
маятника, ![]() —
начальная фаза колебаний,
—
начальная фаза колебаний, ![]() — циклическая
частота,
которая определяется из уравнения
движения. Движение, совершаемое маятником,
называется гармоническими
колебаниями
— циклическая
частота,
которая определяется из уравнения
движения. Движение, совершаемое маятником,
называется гармоническими
колебаниями
[Править]Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
![]()
где ![]() —
это синус
Якоби.
Для
—
это синус
Якоби.
Для ![]() он
является периодической функцией, при
малых
он
является периодической функцией, при
малых ![]() совпадает
с обычным тригонометрическим синусом.
совпадает
с обычным тригонометрическим синусом.
Параметр определяется выражением
![]()
где ![]() —
энергия маятника в единицах t−2.
—
энергия маятника в единицах t−2.
Период колебаний нелинейного маятника
![]()
где K — эллиптический интеграл первого рода.
Для вычислений практически удобно разлагать эллиптический интеграл в ряд:
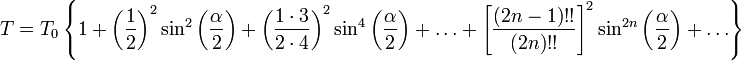 ,
где
,
где 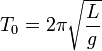 — период
малых колебаний,
— период
малых колебаний, ![]() — максимальный
угол отклонения маятника от вертикали.
— максимальный
угол отклонения маятника от вертикали.
При углах до 1 радиана (≈60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:
![]() .
.
Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах 1096-1097 Сентябрьского выпуска заметок американского математического общества 2012 г.[3]:
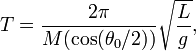
где ![]() -- арифметико-геометрическое
среднее числел
1 и
-- арифметико-геометрическое
среднее числел
1 и ![]() .
.
Физический маятник, дифференциальное уравнение его движения и период колебаний.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
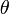 —
угол
отклонения маятника от равновесия;
—
угол
отклонения маятника от равновесия;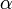 —
начальный
угол отклонения маятника;
—
начальный
угол отклонения маятника;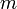 —
масса
маятника;
—
масса
маятника;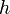 —
расстояние
от точки подвеса до центра тяжести
маятника;
—
расстояние
от точки подвеса до центра тяжести
маятника; —
радиус
инерции относительно оси, проходящей
через центр тяжести.
—
радиус
инерции относительно оси, проходящей
через центр тяжести.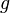 —
ускорение
свободного падения.
—
ускорение
свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:
![]() .
.
Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
![]() .
.
Полагая ![]() ,
предыдущее уравнение можно переписать
в виде:
,
предыдущее уравнение можно переписать
в виде:
![]() .
.
Последнее
уравнение аналогично уравнению
колебаний математического
маятника длиной ![]() .
Величина
называется приведённой
длиной физического
маятника.
.
Величина
называется приведённой
длиной физического
маятника.
Период колебаний физического маятника
Для
того, чтобы найти период колебаний
физического маятника, необходимо решить
уравнение качания.
Для этого умножим
левую 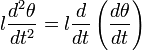 и
правую часть этого уравнения на
и
правую часть этого уравнения на ![]() .
Тогда:
.
Тогда:
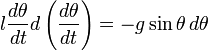 .
.
Интегрируя это уравнение, получаем.
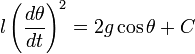 ,
,
где ![]() произвольная
постоянная. Её можно найти из граничного
условия, что в моменты
произвольная
постоянная. Её можно найти из граничного
условия, что в моменты ![]() .
Получаем:
.
Получаем: ![]() .
Подставляем и преобразовываем получившееся
уравнение:
.
Подставляем и преобразовываем получившееся
уравнение:
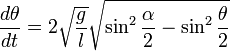 .
.
Отделяем переменные и интегрируем это уравнение:
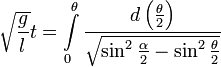 .
.
Удобно
сделать замену переменной, полагая ![]() .
Тогда искомое уравнение принимает вид:
.
Тогда искомое уравнение принимает вид:
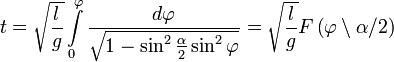 .
.
Здесь ![]() — нормальный
эллиптический интеграл Лежандра 1-го
рода.
Для периода колебаний получаем формулу:
— нормальный
эллиптический интеграл Лежандра 1-го
рода.
Для периода колебаний получаем формулу:
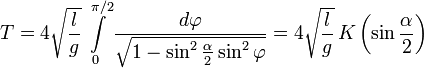 .
.
Здесь ![]() — полный
нормальный эллиптический интеграл
Лежандра 1-го рода.
Раскладывая его в ряд, можно получить
удобную для практических вычислений
формулу:
— полный
нормальный эллиптический интеграл
Лежандра 1-го рода.
Раскладывая его в ряд, можно получить
удобную для практических вычислений
формулу:
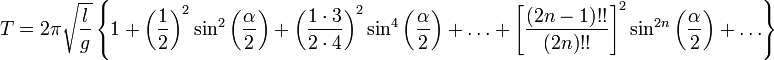
Свободные гармонические колебания в электрическом колебательном контуре. Формула Томсона.
Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L,конденсатора емкостью С и резистора сопротивлением R.
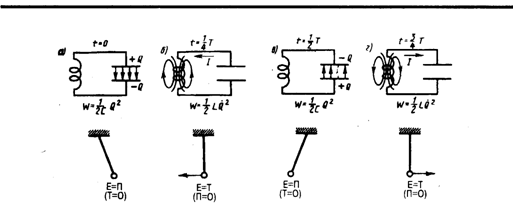
Рассмотрим
последовательные стадии колебательного
процесса в идеализированном контуре,
сопротивление которого пренебрежимо
мало (R0).
Для возбуждения в контуре колебаний
конденсатор предварительно заряжают,
сообщая его обкладкам заряды ±Q.
Тогда в начальный момент времени t=0
(рис. 202,а) между
обкладками конденсатора возникнет
электрическое поле, энергия которого ![]() Q2 (см.
(95.4)). Если замкнуть конденсатор на
катушку индуктивности, он начнет
разряжаться, и в контуре потечет
возрастающий со временем ток I.
В результате энергия электрического
поля будет уменьшаться, а энергия
магнитного поля катушки (она
равна
Q2 (см.
(95.4)). Если замкнуть конденсатор на
катушку индуктивности, он начнет
разряжаться, и в контуре потечет
возрастающий со временем ток I.
В результате энергия электрического
поля будет уменьшаться, а энергия
магнитного поля катушки (она
равна ![]() — возрастать.
— возрастать.
Так как R0, то, согласно закону сохранения энергии, полная энергия
![]()
так как она на нагревание не расходуется. Поэтому в момент t=¼T, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения (рис. 202, б). Начиная с этого момента ток в контуре будет убывать; следовательно, начнет ослабевать магнитное поле катушки, и в ней индуцируется ток, который течет (согласно правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который в конце концов обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 202, в). Далее те же процессы начнут протекать в обратном направлении (рис. 202, г) и система к моменту времени t=Т придет в первоначальное состояние (рис. 202, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. Если бы потерь энергии не было, то в контуре совершались бы периодические незатухающие колебания, т.е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей.
Электрические колебания в колебательном контуре можно сопоставить с механическими колебаниями маятника (рис. 202 внизу), сопровождающимися взаимными превращениями потенциальной и кинетической энергий маятника. В данном случае энергия электрического поля конденсатора (Q2/(2C)) аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ2/2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L играет роль массы т, а сопротивление контура — роль силы трения, действующей на маятник.
Согласно закону Ома, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор сопротивлением R,
![]()
где IR — напряжение
на резисторе, Uc=Q/C — напряжение
на конденсаторе, ![]() –
э.д.с. самоиндукции, возникающая в катушке
при протекании в ней переменного тока
(
–
э.д.с. самоиндукции, возникающая в катушке
при протекании в ней переменного тока
(![]() –
единственная э.д.с. в контуре). Следовательно,
–
единственная э.д.с. в контуре). Следовательно,
![]() (143.1)
(143.1)
Разделив
(143.1) на L и
подставив ![]() получим
дифференциальное уравнение колебаний
заряда Q в
контуре:
получим
дифференциальное уравнение колебаний
заряда Q в
контуре:
![]() (143.2)
(143.2)
В данном колебательном контуре внешние э.д.с. отсутствуют, поэтому рассматриваемые колебания представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда из (143.2) получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре.
![]()
Из выражений (142.1) и (140.1) вытекает, что заряд Q совершает гармонические колебания по закону
![]() (143.3)
(143.3)
где Qm — амплитуда колебаний заряда конденсатора с циклической частотой 0, называемой собственной частотой контура, т. е.
![]() (143.4)
(143.4)
и периодом
![]() (143.5)
(143.5)
Формула (143.5) впервые была получена У. Томсоном и называется формулой Томсона. Сила тока в колебательном контуре (см. (140.4))
![]() (143.6)
(143.6)
где Im=0Qm — амплитуда силы тока. Напряжение на конденсаторе
![]() (143.7)
(143.7)
где Um=Qm/C — амплитуда напряжения.
Из выражений (143.3) и (143.6) вытекает, что колебания тока I опережают по фазе колебания заряда Q на /2, т.е., когда ток достигает максимального значения, заряд (а также и напряжение (см. (143.7)) обращается в нуль, и наоборот.
Энергия свободных гармонических колебаний (механических и электромагнитных)
МЕХАНИЧЕСКИХ
Вычислим энергию тела массой m, совершающего гармонические колебания с амплитудой А и круговой частотой ω (рис. 1.1).
Потенциальная энергия U тела, смещенного на расстояние х от положения равновесия, измеряется той работой, которую произведет возвращающая сила , перемещая тело в положение равновесия.
, отсюда , или
|
, |
(1.5.1) |
|
|
|
(1.5.2) |
|
Например, баллистический маятник приходит в движение при попадании в него пули.
Кинетическая энергия
|
. |
(1.5.3) |
|
Заменив в (1.5.2) и сложив почленно уравнения (1.5.2) и (1.5.3), получим выражение для полной энергии:
, или
|
. |
(1.5.4) |
|
Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания.
В случае свободных незатухающих колебаний полная энергия не зависит от времени, поэтому и амплитуда А не зависит от времени.
Из (1.5.2) и (1.5.3) видно, что и потенциальная U, и кинетическая K энергия пропорциональны квадрату амплитуды А2.
Рассмотрим колебания груза под действием сил тяжести (рис. 1.4).
Рис. 1.4
Из рис. 1.4 и из формул (1.5.2) и (1.5.3) видно, что U и K изменяются периодически (при свободных незатухающих колебаниях). Однако период изменения энергии в два раза меньше, чем период изменения смещения скорости и ускорения. Это значит, что и кинетическая, и потенциальная энергия изменяются с частотой, которая в два раза превышает частоту смещения гармонического колебания. За время одного полного колебания U и K дважды достигают своих максимальных значений и дважды обращаются в нуль. Связано это с тем, что и U, и K пропорциональны квадрату косинуса и синуса фазы колебаний.
Максимум потенциальной энергии (1.5.2) .
Максимум кинетической энергии , но когда и наоборот. На рис. 1.5 представлены графики зависимости х, U и K от времени t.
Рис. 1.5 Рис. 1.6
При колебаниях, совершающихся под действием потенциальных (консервативных) сил, происходит переход кинетической энергии в потенциальную и наоборот, но их сумма в любой момент времени постоянна.
На рис. 1.6 приведена кривая потенциальной энергии.
Горизонтальная линия соответствует определенному значению полной энергии: Расстояние от этой линии до кривой равно кинетической энергии, а движение ограничено значениями х, заключенными в пределах от + А до – А. Эти результаты полностью согласуются с полным решением уравнения движения.
ЭЛЕКТРАМАГНИТНЫХ
Среди исследований различных электрических явлений особое место занимают исследования электромагнитных колебаний. При колебательном процессе электрические физические величины (заряды, токи) периодически изменяются и процесс сопровождается взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний применяется колебательный контур — цепь, которая состоит из последовательно включенных резистора сопротивлением R, катушки индуктивностью L, и конденсатора емкостью С. Исследуем последовательные стадии колебательного процесса в идеализированном контуре, у которого сопротивление пренебрежимо мало (R≈0). Для возбуждения колебаний в контуре конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Следовательно, в начальный момент времени t=0 (рис. 1а) между обкладками конденсатора появится электрическое поле, энергия которого равна Q2/(2C) . Если конденсатор замкнуть на катушку индуктивности, то он начнет разряжаться, и в контуре начнет течь возрастающий со временем ток I. В результате энергия электрического поля будет падать, а энергия магнитного поля катушки (она равна (1/2)LI2 ) - увеличиваться.
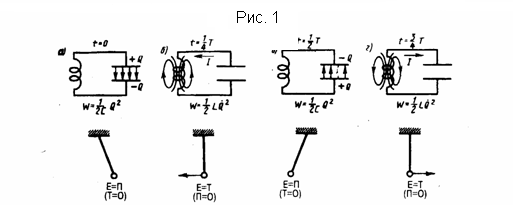
Так
как R≈0, то, используя закон сохранения
энергии, полная энергия
![]() поскольку
полная энергия на нагревание не тратится.
Поэтому в момент t=(1/4)T, когда конденсатор
полностью разрядится, энергия
электрического поля станет равной нулю,
а энергия магнитного поля (а следовательно,
и ток) достигает максимального значения
(рис. 1б). Далее, начиная с этого момента
ток в контуре будет уменьшаться; значит,
начнет уменьшаться магнитное поле
катушки, и в ней индуцируется ток, который
течет (по правилу Ленца) в том же
направлении, что и ток разрядки
конденсатора. Далее, начнет перезаряжаться
конденсатор, появится электрическое
поле, которое будет стремиться ослабить
ток, который в конце концов станет равным
нулю, а заряд на обкладках конденсатора
станет максимальным (рис. 1в). Далее те
же процессы будут протекать в обратном
направлении (рис. 1г) и к моменту времени
t=Т система придет в первоначальное
состояние (рис. 1а). После этого рассмотренный
цикл разрядки и зарядки конденсатора
будет повторяться. Если бы в контуре
потерь энергии не было, то совершались
бы периодические незатухающие колебания,
т.е. периодически изменялись (колебались)
бы заряд Q на обкладках конденсатора,
сила тока I, текущего через катушку
индуктивности и напряжение U на
конденсаторе . Значит, в контуре появляются
электрические колебания, причем колебания
сопровождаются превращениями энергий
электрического и магнитного полей.
С
электрическими колебаниями в колебательном
контуре можно провести аналогию с
механическими колебаниями маятника
(рис. 1 внизу), которые сопровождаются
взаимными превращениями кинетической
и потенциальной энергий маятника (на
рисунке Е - кинетическая энергия, П -
потенцияльная). В данном случае энергия
электрического поля конденсатора
Q2/(2C)
аналогична потенциальной энергии
маятника, энергия магнитного поля
катушки (LQ2/2)
— кинетической энергии, сила тока в
контуре — скорости движения маятника.
Индуктивность L аналогична массе m, а
сопротивление контура — силе трения,
которая действуюет на маятник.
По
закону Ома, для контура, который содержит
резистор сопротивлением R, катушку
индуктивностью L, и конденсатор емкостью
С
поскольку
полная энергия на нагревание не тратится.
Поэтому в момент t=(1/4)T, когда конденсатор
полностью разрядится, энергия
электрического поля станет равной нулю,
а энергия магнитного поля (а следовательно,
и ток) достигает максимального значения
(рис. 1б). Далее, начиная с этого момента
ток в контуре будет уменьшаться; значит,
начнет уменьшаться магнитное поле
катушки, и в ней индуцируется ток, который
течет (по правилу Ленца) в том же
направлении, что и ток разрядки
конденсатора. Далее, начнет перезаряжаться
конденсатор, появится электрическое
поле, которое будет стремиться ослабить
ток, который в конце концов станет равным
нулю, а заряд на обкладках конденсатора
станет максимальным (рис. 1в). Далее те
же процессы будут протекать в обратном
направлении (рис. 1г) и к моменту времени
t=Т система придет в первоначальное
состояние (рис. 1а). После этого рассмотренный
цикл разрядки и зарядки конденсатора
будет повторяться. Если бы в контуре
потерь энергии не было, то совершались
бы периодические незатухающие колебания,
т.е. периодически изменялись (колебались)
бы заряд Q на обкладках конденсатора,
сила тока I, текущего через катушку
индуктивности и напряжение U на
конденсаторе . Значит, в контуре появляются
электрические колебания, причем колебания
сопровождаются превращениями энергий
электрического и магнитного полей.
С
электрическими колебаниями в колебательном
контуре можно провести аналогию с
механическими колебаниями маятника
(рис. 1 внизу), которые сопровождаются
взаимными превращениями кинетической
и потенциальной энергий маятника (на
рисунке Е - кинетическая энергия, П -
потенцияльная). В данном случае энергия
электрического поля конденсатора
Q2/(2C)
аналогична потенциальной энергии
маятника, энергия магнитного поля
катушки (LQ2/2)
— кинетической энергии, сила тока в
контуре — скорости движения маятника.
Индуктивность L аналогична массе m, а
сопротивление контура — силе трения,
которая действуюет на маятник.
По
закону Ома, для контура, который содержит
резистор сопротивлением R, катушку
индуктивностью L, и конденсатор емкостью
С
![]() где
IR—напряжение на резисторе, UC =
Q/C - напряжение на конденсаторе, ξs =
-L(dI/dt) – э.д.с. самоиндукции, которая
возникает в катушке при протекании в
ней переменного тока (ξs –
единственная э.д.с. в контуре).
Значит,
где
IR—напряжение на резисторе, UC =
Q/C - напряжение на конденсаторе, ξs =
-L(dI/dt) – э.д.с. самоиндукции, которая
возникает в катушке при протекании в
ней переменного тока (ξs –
единственная э.д.с. в контуре).
Значит,
![]() (1)
Разделив
формулу (1) на L и подставив
(1)
Разделив
формулу (1) на L и подставив ![]() и
и ![]() получим
дифференциальное уравнение колебаний
заряда Q в контуре:
получим
дифференциальное уравнение колебаний
заряда Q в контуре:
![]() (2)
В
рассматриваемом колебательном контуре
внешние э.д.с. отсутствуют, значит
колебания в контуре представляют
собой свободныеколебания.
Если сопротивление R=0, то свободные
электромагнитные колебания в контуре
будут гармоническими.
Тогда из (2) найдем дифференциальное
уравнение свободных гармонических
колебаний заряда в контуре:
(2)
В
рассматриваемом колебательном контуре
внешние э.д.с. отсутствуют, значит
колебания в контуре представляют
собой свободныеколебания.
Если сопротивление R=0, то свободные
электромагнитные колебания в контуре
будут гармоническими.
Тогда из (2) найдем дифференциальное
уравнение свободных гармонических
колебаний заряда в контуре:
![]() Из
формулы (1) следует, что заряд Q гармонически
колеблеься по закону
Из
формулы (1) следует, что заряд Q гармонически
колеблеься по закону
![]() (3)
где
Qm —
амплитуда колебаний заряда конденсатора
с циклической частотой ω0,
которая называется собственной
частотой контура,
т. е.
(3)
где
Qm —
амплитуда колебаний заряда конденсатора
с циклической частотой ω0,
которая называется собственной
частотой контура,
т. е.
![]() (4)
и
периодом
(4)
и
периодом
![]() (5)
Выражение
(5) впервые было получено У. Томсоном и
называется формулой
Томсона.
Сила тока в колебательном контуре
(5)
Выражение
(5) впервые было получено У. Томсоном и
называется формулой
Томсона.
Сила тока в колебательном контуре
![]() (6)
где
Im =
ω0Qm —
амплитуда силы тока. Напряжение на
конденсаторе равно
(7)
где
Um=Qm/C
- амплитуда напряжения.
Из
формул (3) и (6) вытекает, что колебания
тока I опережают по фазе колебания заряда
Q на π/2, т.е., когда ток равен максимальному
значению, заряд (а также и напряжение
(7)) обращается в нуль, и наоборот.
(6)
где
Im =
ω0Qm —
амплитуда силы тока. Напряжение на
конденсаторе равно
(7)
где
Um=Qm/C
- амплитуда напряжения.
Из
формул (3) и (6) вытекает, что колебания
тока I опережают по фазе колебания заряда
Q на π/2, т.е., когда ток равен максимальному
значению, заряд (а также и напряжение
(7)) обращается в нуль, и наоборот.
