Лекция № 2. Системы счисления
Разные народы в разные времена использовали разные системы счисления. Следы древних систем счета встречаются и сегодня в культуре многих народов. К древнему Вавилону восходит деление часа на 60 минут и угла на 360 градусов. К Древнему Риму - традиция записывать в римской записи числа I, II, III и т. д. К англосаксам - счет дюжинами: в году 12 месяцев, в футе 12 дюймов, сутки делятся на 2 периода по 12 часов.
По современным данным, развитые системы нумерации впервые появились в древнем Египте. Для записи чисел египтяне применяли иероглифы один, десять, сто, тысяча и т.д. Все остальные числа записывались с помощью этих иероглифов и операции сложения.
В конце концов, самой популярной системой счисления оказалась десятичная система. Десятичная система счисления пришла из Индии, где она появилась не позднее VI в. н. э. В ней всего 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 но информацию несет не только цифра, но также и место позиция, на которой она стоит. В числе 444 три одинаковых цифры обозначают количество и единиц, и десятков, и сотен. А вот в числе 400 первая цифра обозначает число сотен, два 0 сами по себе вклад в число не дают, а нужны лишь для указания позиции цифры 4.
Основные понятия систем счисления
Системой счисления называется совокупность приемов обозначения чисел - язык, алфавитом которого являются символы (цифры), а синтаксисом - правило, позволяющее сформулировать запись чисел однозначно. Запись числа в некоторой системе счисления называется кодом числа. Общий вид числа:
A = anan-1...a2a1a0
Отдельную позицию в изображении числа принято называть разрядом, а номер позиции - номером разряда. Число разрядов в записи числа называется разрядностью и совпадает с его длиной.
-
1
0
0
1
0
1
1
0
0 1 2 3 4 5 6 7 8
В техническом аспекте длина числа интерпретируется как длина разрядной сетки.
Диапазон представления D чисел в данной системе счисления - это интервал числовой оси, заключенной между минимальным и максимальным числами, представленными заданными разрядами.
Любая система счисления, предназначенная для практического использования, должна обеспечивать:
возможность представления числа в заданном диапазоне чисел;
однозначность представления;
краткость и простота записи чисел;
легкость овладения системой, а также простота и удобство оперирования ею.
Таким
образом, система счисления - это
совокупность правил и приемов записи
чисел с помощью набора цифровых знаков.
Количество цифр, необходимых для записи
числа в системе, называют основанием
системы счисления. Основание системы
записывается в справа числа в нижнем
индексе:
и т. д.
Различают два типа систем счисления:
позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена:
где
S - основание системы счисления;
-
цифры числа, записанного в данной системе
счисления;
n - количество разрядов числа.
Пример. Число
запишется
в форме многочлена следующим образом:
Виды систем счисления
Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква - V пять, X - десять, L - пятьдесят, C - сто, D - пятьсот, M - тысячу и т.д. Например, число 264 записывается в виде CCLXIV. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 3.1. Запись чисел в римской системе счисления
1 |
2 |
3 |
4 |
5 |
I |
II |
III |
IV |
V |
6 |
7 |
8 |
9 |
10 |
VI |
VII |
VIII |
IX |
X |
11 |
13 |
18 |
19 |
22 |
XI |
XIII |
XVIII |
XIX |
XXII |
34 |
39 |
40 |
60 |
99 |
XXXIV |
XXXIX |
XL |
LX |
XCIX |
200 |
438 |
649 |
999 |
1207 |
CC |
CDXXXVIII |
DCXLIX |
CMXCIX |
MCCVII |
2045 |
3555 |
3678 |
3900 |
3999 |
MMXLV |
MMMDLV |
MMMDCLXXVIII |
MMMCM |
MMMCMXCIX |
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Десятичная система счисления – в настоящее время наиболее известная и используемая. Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника. Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Люди привыкли считать в десятичной системе счисления, потому что у них по 10 пальцев на руках.
Древнее изображение десятичных цифр (рис.3.1) не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 - углов нет, 1 - один угол, 2 - два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.
Рис.3.1. Древнее изображение десятичных чисел
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции. В ранних индийских рукописях, дошедших до нас, числа записывались в обратном порядке - наиболее значимая цифра ставилась справа. Но вскоре стало правилом располагать такую цифру с левой стороны. Особое значение придавалось нулевому символу, который вводился для позиционной системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе индусские приёмы десятичной арифметики получили распространение в начале ХIII в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне.
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система счисления, её основание - число 2. Для записи чисел в этой системе используют только две цифры - 0 и 1. Вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, еще в ХVII - ХIХ веках. Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.
Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы - триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.
С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки - точки и тире, может передать практически любой текст.
Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной - восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.
Таблица 3.2. Соответствие чисел, записанных в различных системах счисления
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
1 |
001 |
1 |
1 |
2 |
010 |
2 |
2 |
3 |
011 |
3 |
3 |
4 |
100 |
4 |
4 |
5 |
101 |
5 |
5 |
6 |
110 |
6 |
6 |
7 |
111 |
7 |
7 |
8 |
1000 |
10 |
8 |
9 |
1001 |
11 |
9 |
10 |
1010 |
12 |
A |
11 |
1011 |
13 |
B |
12 |
1100 |
14 |
C |
13 |
1101 |
15 |
D |
14 |
1110 |
16 |
E |
15 |
1111 |
17 |
F |
16 |
10000 |
20 |
10 |
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 3.3. Степени числа 2
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
Пример.
Число
перевести
в десятичную систему счисления.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 3.4. Степени числа 8
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
Пример. Число
перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 3.5. Степени числа 16
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
16 |
256 |
4096 |
65536 |
1048576 |
16777216 |
Пример. Число
перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число
перевести
в двоичную систему счисления.
-
22
2
22
11
2
0
10
5
2
1
4
2
2
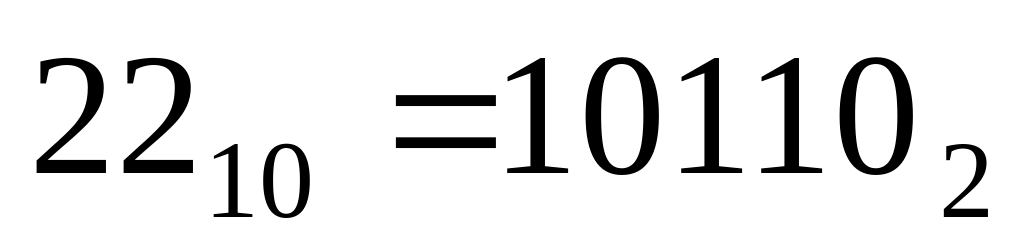
1
2
1
0
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример.
Число
перевести в восьмеричную систему
счисления.
-
571
8
56
71
8
11
8
64
7
8
8
8
1
3
0
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число
перевести в шестнадцатеричную систему
счисления.
-
7467
16
7456
466
16
11
464
29
16
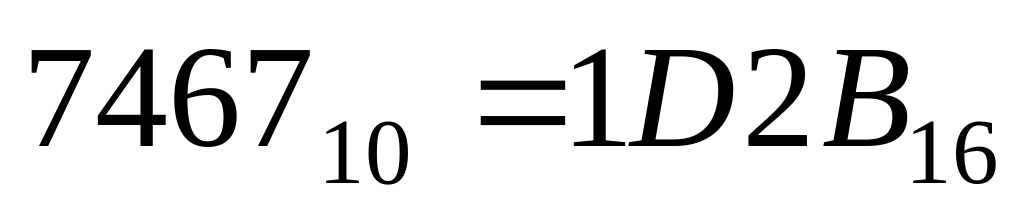
2
16
1
13
7. Для перехода от двоичной к восьмеричной системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду заменяют соответствующей восьмеричной цифрой (табл.3.2).
Пример.
Перевести 1101111001.11012
"8"
с.с.
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей шестнадцатеричной цифрой (табл. 3.2.).
Пример. Перевести 11111111011.1001112 "16" с.с.
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример. Перевести 305.48 "2" с.с.
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Перевести 7B2.E16 "2" с.с.
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример. Перевести 175.248 "16" с.с.
Результат: 175.248 = 7D.516.
Правила перевода дробных чисел из одной системы счисления в другую
Правило 1. Перевод правильной дроби:
Перевод правильной дроби, представленной в с/с с основанием R, в с/с с основанием Q заключается в последовательном умножении этой дроби на основание Q по правилам системы счисления с основанием R, причем перемножают только дробные части. Дробь N в с/с с основанием Q представляется в виде упорядоченной последовательности целых частей произведений в порядке их получения. (Иными словами, старший разряд является первой цифрой произведения). Количество последовательных произведений определяет количество цифр в полученном числе.
Для многих чисел указанный процесс умножения потенциально никогда не кончается. Поэтому он продолжается до тех пор, пока не будет получено необходимое число цифр дробной части. При переводе числа с целью представления ее в “машинной” форме можно точно указать требуемое количество цифр.
Переведём в двоичную систему счисления десятичную дробь 0,7243. Основание исходной системы счисления R=10. Основание новой системы счисления Q=2. Согласно приведенного правила исходное число 0,7243 надо умножать на основание новой системы (на 2) по правилам десятичной системы счисления (исходная с/с). Выполним серию умножений до получения, например, шести цифр в двоичном числе:
Искомые цифры дроби:
0,7243 * 2 = 1,4486 1 - Старшая цифра.
0,4486 * 2 = 0,8972 0
0,8942 * 2 = 1,7944 1
0,7944 * 2 = 1,5888 1
0,5888 * 2 = 1,1776 1
0,1776 * 2 = 0,3552 0
0,3552 * 2 = 0,7104 0
Искомое представление число 0,7243 в двоичной системе счисления = 0,101110.
Для получения шести цифр дроби выполнено семь умножений. Это связано с необходимостью выполнить округление, чтобы представить дробь заданной длины более точно.
Из последнего примера, конечная дробь в одной системе счисления может стать бесконечной в другой. Это утверждение справедливо для всех случаев, когда одна система счисления не может быть получена возведением в целую степень основания другой.
Примеры.
1. Десятичная дробь 0,2 представляется бесконечной дробью 0,33333... в шестнадцатеричной системе счисления (основания с/с 10 и 16).
2. Шестнадцатеричная дробь 0,131 представляется конечной дробью 0,10110001 в двоичной системе счисления (основания с/с 16 и 2).
Правило 2. Перевод неправильной дроби:
Перевод неправильной дроби из одной системы счисления в другую осуществляется отдельно для целой и дробной части по правилам, изложенным выше.
Примеры: Перевод из одной системы в другую.
-
173
8
11
2
5
21
8
1
5
2
5
2
1
2
2
0
1
Перевод дробных чисел из одной системы в другую.
-
0
65625
* 8
0
65625
* 16
0
5625
* 2
5
25000
* 8
10
(А)
50000
* 16
1
1250
* 2
2
00000
8
00000
0
2500
* 2
0
5000
* 2
1
0000
Арифметические операции в позиционной системе счисления.
Сложение чисел в двоичной системе счисления.
Арифметические операции во все позиционных системах счисления выполняются по одним и тем же правилам. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел.
+ |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
10 |
Рассмотрим арифметические действия в двоичной системе счисления. Сначала отметим, что 12+12=102. Почему? Во-первых, вспомним, как в привычной десятичной системе счисления появилась запись 10. К количеству, обозначенному старшей цифрой десятичного алфавита 9, прибавляем 1. Получается количество, для обозначения которого одной цифрой в алфавите цифр уже не осталось. Приходится для полученного количества использовать комбинацию двух цифр алфавита, то есть представлять данное количество наименьшим из двухразрядных чисел: 910+110=1010. Аналогичная ситуация складывается в случае двоичной системы счисления. Здесь количество, обозначенное старшей цифрой 12 двоичного алфавита, увеличивается на единицу. Чтобы полученное количество представить в двоичной системе счисления, также приходится использовать два разряда. Для наименьшего из двухразрядных чисел здесь тот же единственный вариант: 102. Во-вторых, важно понять, что 102 1010. Строго говоря, в двоичной системе счисления это и читать надо не “десять”, а “один ноль”. Верным является соотношение 102 = 210. Здесь слева и справа от знака равенства написаны разные обозначения одного и того же количества. Это количество просто записано с использованием алфавитов разных систем счисления – двоичной и десятичной. Вроде, как мы на русском языке скажем “яблоко”, а на английском про тот же предмет – “apple”, и будем правы в обоих случаях.
Пример:
2 10 0000000000000010 +3 +11 + 0000000000000011 5 101 0000000000000101
При сложении чисел надо обязательно проговаривать алгоритм сложения. Следует учитывать, что сложение, как обычно, нужно начинать с младшего разряда. Если сумма единиц разряда окажется равной или большей основания системы счисления, то возникает перенос единицы в старший разряд. После сложения cледует обязательно сделать обратный перевод и убедиться, что число 101 — действительно число 5 в десятичной системе счисления.
Вычитание двоичных чисел.
- |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Исходя из того, что вычитание есть действие, обратное сложению, запишем правило арифметического вычитания одноразрядных чисел в двоичной системе счисления:
0 – 0=0; 1 – 0=1; 1 – 1=0; 10 – 1=1.
Используя это правило, можно проверить правильность произведенного выше сложения вычитанием из полученной суммы одного из слагаемых. При этом, чтобы вычесть в каком-либо разряде единицу из нуля, необходимо “занимать” недостающее количество в соседних старших разрядах (так же, как в десятичной системе счисления поступают при вычитании большего числа из меньшего).
Вычитание. При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и ставится соответствующий знак. В таблице вычитания 1 с чертой означает заем в старшем разряде.
Пример. Рассмотрим несколько примеров вычитания двоичных чисел:
10111001,1-10001101,1=101100,0
101011111-110101101= -1001110
В компьютере вычитание заменяется сложением с отрицательным числом, представленным в дополнительном коде. Запись на доске:
14 1110 0000000000001110 -9 +1001 +1111111111110111 5 101 10000000000000101
Так как под целое число отводится 16 разрядов, то старшая единица теряется. Ответ получается 101.
Умножение чисел в двоичной системе счисления.
* |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
Правила умножения одноразрядных двоичных чисел наиболее очевидны:
0 0=0; 1 0=0; 0 1=0; 1 1=1.
Умножение. Операция умножения выполняется с использованием таблицы умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя.
Пример. Рассмотрим несколько примеров умножения двоичных чисел:
11001*1101=101000101
11001,01*11,01=1010010,0001
110 *101 110 + 000 110 11110
Подчеркиваем, что при умножении 1•1 = 1 и 1•0 = 0. Анализируя примеры умножения в двоичной системе счисления, необходимо обратить внимание учащихся на важную особенность выполнения этой операции в данной системе счисления. Так как очередная цифра множителя может быть только 1 или 0, то промежуточное произведение равно либо множимому, либо 0. Таким образом, операция умножения в двоичной системе фактически не производится: в качестве промежуточного произведения записывается либо множимое, либо 0, а затем промежуточные произведения суммируются. Иначе говоря, операция умножения заменяется последовательным сложением.
Контрольные вопросы
Что называется системой счисления?
На какие два типа можно разделить все системы счисления?
Какие системы счисления называются позиционными?
Что такое двоичная система счисления?
По каким правилам выполняется сложение двух положительных чисел?
Переведите в двоичную систему счисления десятичные числа: 231, 564, 1023.