5 .9.2. Эллипс
Определение 5.4
Геометрическое
место точек, для каждой из которых
__________________ до двух данных точек
и
,
называемых его _____________, есть величина
____________________, называется __________________.
О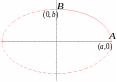
тметим
на оси
две точки:
,
т.е.
(___________ __________________). Пусть
- произвольная точка эллипса.
________________________
(
)
точки
эллипса называются ____________________
____________________________________________
_______________________
(5.14) |
|
– ______________________________________
Отрезок
называется ____________________,
отрезок
называется ____________________.
Замечание 6. Уравнение (5.14) можно рассматривать и в случае ________, тогда - _______________ и фокусы эллипса ___________________
Замечание 7. В случае, когда ___________, уравнение (5.14) вырождается в ________________с центром в ______________________________________
Если центр эллипса
перенести в точку
,
то уравнение эллипса примет вид:
Замечание 8. Уравнение __________ определяет ____________ эллипс.
Уравнение ____________ определяет ______________.
Алгебраическое уравнение (5.12) определяет эллипс, если
____________. (**)
Пример 5.4. Уравнение
эллипса
привести
к каноническому виду.
Решение.
5 .9.3. Гипербола
Определение 5.5
Геометрическое место точек, абсолютная величина __________ каждой из которых до двух данных точек и , называемых его фокусами, есть величина _______________, и называется ____________________, т.е.
(5.15)
– _______________________________
– _________________________________
П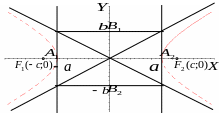
ри
построении гиперболы необходимо
построить прямоугольник со сторонами
__ и __ и провести диагонали, которые и
являются __________ (см. рис.).
,
– _______________,
– ____________________,
– _________________,
– ________________________.
Если _____, то гипербола называется ___________________, ее уравнение имеет вид:
Замечание 8. Уравнение
(5.16)
определяет гиперболу ______________________________
Гиперболы, определяемые уравнениями (5.15) и (5.16), называются __________________________
Если центр гипербол
перенести в точку
,
то уравнение примет вид:
Замечание 9. Уравнение ___________ определяет ___________________
Можно выяснить при каких коэффициентах уравнение (5.12) будет определять гиперболу или семейство прямых. По аналогии с эллипсом в уравнении (5.12)
__________________ (***)
5.9.4. Парабола
Определение 5.6
______________ называется геометрическое место точек, равноудаленных ___________, называемой _____________ и точки, называемой _________
Пусть дано: ______________________________________
(5.17)
– _________________________________________
Здесь ____________________________________________________________ _____________________________________________________________
Если фокус параболы расположен ____________, то уравнение будет иметь вид: ____________.
– _____________________________________________
Замечание 10. Частные случаи: а) _________________________________
б) ______________________________________________
в) ______________________________________________
Уравнение (5.12) определяет параболу, если ____________. (****)