Лекция 5

Раздел III. Аналитическая геометрия

§1. Аналитическая геометрия на плоскости

5.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

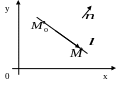П усть , .

Найти: уравнение прямой , проходящей через точку перпендикулярно вектору (см. рис.)

Назовем _____________________________.

Выберем на произвольную точку .

Найдем координаты . Т.к. , то ___________

(5.1)

– уравнение прямой , ___________________________________________

__________________________________________________________

5.2. Общее уравнение прямой

Из уравнения 5.1 с помощью элементарных преобразований получим:

_________________________________________________________________

(5.2)

– ____________________________________.

Частные случаи уравнения (5.2)

1) _____________, 2) ______________, 3) ______________, 4) ____________,

5) __________________.

5 .3. Уравнение прямой с угловым коэффициентом

Пусть . Разрешим общее уравнение прямой (5.2) относительно : ___________ . Пусть ____________, тогда

_________________________________________ (5.3)

где ___ – угловой коэффициент прямой, _____ – отрезок, который отсекает данная прямая на оси .

Замечание 1. Если _____, то _____ – прямая проходит ______________ _________________; если _____, то ______ – семейство прямых, ___________________________________________

5.4. Параметрические и канонические уравнения прямой

Определение 5.1

Всякий ___________вектор ________________ прямой называется ______________________________ этой прямой.

П усть точка , тогда произвольная точка лишь при условии, когда вектор ____________ . Это означает, что ________________

Если обозначить радиус-вектора точек , через __ и __, соответственно, то , тогда:

____________

Если ______________________________, то в координатах запишется:

(5.4)

– ______________________ прямой на плоскости, проходящей через точку _________ в направлении _______________.

Исключая из уравнений (5.4) параметр __, получаем:

(5.5)

– ______________________________ прямой.

Замечание 2. Уравнение (5.5) необходимо воспринимать как ________________: если ____, то это прямая, ______________________, проходящая через точку ______.

Замечание 3.

Приведем уравнение (5.5) к общему знаменателю:

________________________________________

– общее уравнение прямой.

1. В задачах ______ часто обозначают __________.

2. __________________________________________________________ ______________

Вместе с каноническим уравнением (5.5) используется уравнение прямой, _______________________________: если , , то

.

Можно в качестве _________________ вектора принять __________, тогда:

(5.6)

– уравнение прямой, ______________________________________________.