Примерные вопросы для подготовки к зачету
1.Определение математики. Первичные понятия математики.
2.Пространственные формы. Примеры.
3.Количественные отношения. Примеры.
4.Множества (конечные, бесконечные, пустые). Примеры.
5.Способы задания множеств. Примеры.
6.Отношения между множествами. Примеры.
7.Операции над множествами. Примеры.
10.Позиционные и непозиционные системы счисления. Примеры. Отличие.
11.Определение записи натурального числа x в десятичной системе счисления.
12.Л.Ф.Магницкий и его роль в развитии математики в России.
13.Правила округления чисел. Погрешность приближения Абсолютная и относительная погрешности приближения.
14.Наглядное представление результатов исследования.
15.Структура текстовой задачи. Основные методы решения задачи. Этапы решения задачи.
16.Задачи на части и их решение.
17.Величина и ее измерение. Что значит – измерить величину? A=x∙E, A – величина, x - ? E - ?
18.Геометрические фигуры на плоскости, их основные свойства (треугольники, параллельные прямые, параллелограммы, трапеции, квадрат, окружность, ромб).
19.Многогранники (призма, пирамида, параллелепипед, прямоугольный параллелепипед, куб).
20.Тела вращения (цилиндр, конус, сфера, шар).
Образцы тестирования по основным темам программы ен.01 математика Тест №1. Множества и операции над ними
Приведите примеры множеств, составленных из:
названий цветов;
геометрических фигур.
Даны множества:
N – множество всех натуральных чисел;
М – множество натуральных чисел, оканчивающихся цифрой 5;
P – множество четных натуральных чисел.
Укажите,
каким множествам принадлежат числа
18, 225, 317, -130, 18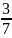
, -16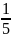
. Запишите это при помощи символа є.
Перечислите и запишите элементы следующих множеств:
М – множество нечетных однозначных чисел;
К – множество натуральных чисел, меньших 5;
S – множество трехзначных чисел, кратных 111;
R – множество целых чисел, больших -3, но меньших 3,7.
Укажите, каким характеристическим свойством обладают элементы каждого из следующих множеств:
А= { а, е ,и, о, у, э, ю, я, ы };
В= {11,22,33,44,55,66,77,88,99}.
Для каждого из слов «сосна», «осколок», «насос», «колос» составьте множество его букв. Имеются ли среди этих множеств равные?
Изобразите отношения между множествами с помощью кругов Эйлера-Венна:
а) А-множество студентов педколледжа, В-множество студентов группы 20у;
б) А-множество студентов педколледжа, С-множество студентов горного колледжа.
Найдите пересечение указанных множеств:
а) Х={a,b,c,d,e} и Y={m,k,d,c,x};
б) Х- множество треугольников, У- множество равнобедренных треугольников.
Найдите объединение множеств:
а) А={х |хєR и 1<х<4} и В={x|xєR и 4≤х≤5};
б) А- множество четырехугольников и В- множество трапеций.
Как можно назвать множество целых корней уравнения: (3х-1)∙(2х-3)=0?
Найдите пересечение множеств:
А- множество делителей числа 12 и
В - множество всех натуральных чисел n, для которых справедливо неравенство n≤7.
Перечислите множество натуральных корней уравнения х2 – 25=0.