
- •Матрицы.
- •Определитель матрицы.
- •Обратная матрица.
- •Системы линейных алгебраических уравнений.
- •Методы решения систем линейных алгебраических уравнений.
- •2. Метод Крамера используется только для решения квадратных систем линейных алгебраических уравнений, которые имеют невырожденную основную матрицу.
- •Матричный метод решения систем линейных алгебраических уравнений.
П90 С.В. Паршина. Конспект лекций по математике: Элементы линейной алгебры / Факультет психологии ЮУрГУ , 2014.
План:
Матрицы. Виды матриц. Линейные операции с матрицами. Транспонирование и умножение матриц. Свойства операций с матрицами.
Определитель матрицы. Свойства определителей. Вычисление определителей.
Обратная матрица. Понятие алгебраического дополнения. Нахождение обратной матрицы. Решение матричных уравнений.
Системы линейных алгебраических уравнений. Основная и расширенная матрицы. Решения системы линейных алгебраических уравнений. Элементарные преобразования систем. Преобразование систем к трапециевидной форме. Исследование систем на совместность.
Методы решения систем линейных алгебраических уравнений. Матричный метод решений систем. Метод Крамера. Метод Гаусса.
Конспект лекций по математике: Элементы линейной алгебры
Матрицы.
Прямоугольная
таблица чисел вида
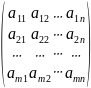 ,
состоящая из
,
состоящая из
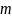 строк
и
строк
и
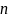 столбцов, называется числовой матрицей
порядка
столбцов, называется числовой матрицей
порядка
 .
Для обозначения матриц обычно используют
большие буквы латинского алфавита
.
Для обозначения матриц обычно используют
большие буквы латинского алфавита
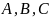 и
т. д.
и
т. д.
Числа
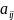 ,
составляющие матрицу, называют ее
элементами, где
,
составляющие матрицу, называют ее
элементами, где
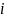 -
это
номер строки,
-
это
номер строки,
 - номер столбца, на пересечении которых
расположен данный элемент.
- номер столбца, на пересечении которых
расположен данный элемент.
Различают
несколько видов матриц. Так, матрица
вида
 ,
порядка
,
порядка
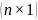 называется
матрицей-столбцом. Соответственно, если
матрица имеет вид
называется
матрицей-столбцом. Соответственно, если
матрица имеет вид
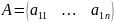 и
порядок
и
порядок
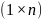 ,
то ее называют матрицей- строкой.
,
то ее называют матрицей- строкой.
Матрица, содержащая одинаковое количество строк и столбцов, называется квадратной матрицей. Порядок квадратной матрицы определяют одним числом по количеству ее строк (столбцов). Например, квадратной матрицей третьего порядка, является матрица
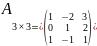 .
.
Совокупность
элементов
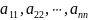 квадратной матрицы, имеющие одинаковый
номер строки и столбца, называют главной
диагональю матрицы.
квадратной матрицы, имеющие одинаковый
номер строки и столбца, называют главной
диагональю матрицы.
Матрица, состоящая из нулей, называется нулевой. Если квадратная матрица состоит из одних нулей, за исключением элементов главной диагонали , она называется диагональной. Например, диагональной матрицей третьего порядка, является матрица
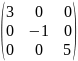 .
.
Диагональная
матрица, у которой главная диагональ
заполнена единицами, называется единичной
и обозначается буквой
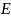 .
Например, единичная матрица второго
порядка имеет вид
.
Например, единичная матрица второго
порядка имеет вид
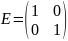 .
.
Кроме перечисленных видов матриц выделяют также матрицы:
1)
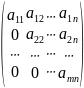 и 2)
и 2)
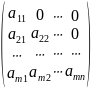 .
.
Первая из них называется верхней треугольной матрицей, а вторая - нижней треугольной. У этих квадратных матриц ниже (выше) главной диагонали все элементы нулевые. Матрицу произвольных размеров вида:

называют трапециевидной.
С матрицами можно проводить различные операции. Выделяют линейные и нелинейные операции. К линейным операциям относятся операция сложения двух матриц и операция умножения матрицы на число.
Так,
суммой двух матриц
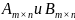 одинакового порядка, называется матрица
одинакового порядка, называется матрица
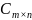 того
же порядка, каждый элемент которой
того
же порядка, каждый элемент которой
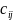 равен
сумме соответствующих элементов
равен
сумме соответствующих элементов
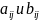 исходных матриц:
исходных матриц:
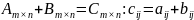 .
.
Произведением
матрицы
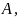 произвольного
порядка, на число α называется матрица
произвольного
порядка, на число α называется матрица
 ,
каждый элемент которой
является
произведением соответствующего элемента
исходной матрицы на это число:
,
каждый элемент которой
является
произведением соответствующего элемента
исходной матрицы на это число:
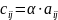 .
.
Например,
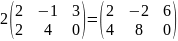 .
.
Матрицу
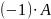 называют противоположной для матрицы
называют противоположной для матрицы
 и обозначают
и обозначают
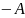 .
.
Операции сложения и умножения матриц на число обладают свойствами, которые мы примем без доказательства:
1.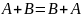
2.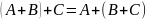
3.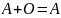
4.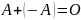
5.
6.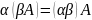
7.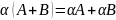
8.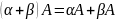 .
.
К нелинейным операциям с матрицами относятся операции умножения двух матриц и транспонирование матриц.
Произведением
матрицы
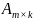 на матрицу
на матрицу
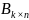 называется матрица
,
каждый элемент которой
называется матрица
,
каждый элемент которой
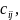 равен сумме произведений элементов
–
ой строки матрицы
на соответствующие элементы
–
ого столбца матрицы
равен сумме произведений элементов
–
ой строки матрицы
на соответствующие элементы
–
ого столбца матрицы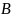 .
.
Например,
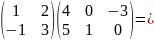
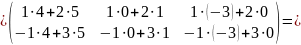

Операция
умножения двух матриц не обладает
законом коммутативности. В общем случае
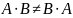 .
Однако, если перемножаются две квадратные
матрицы, одна из которых является
единичной, то в силу определения операции
умножения
.
Однако, если перемножаются две квадратные
матрицы, одна из которых является
единичной, то в силу определения операции
умножения
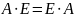 .
.
Произведение матриц, если оно существует, обладает следующими свойствами:
1.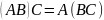
2.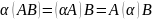
3.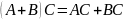
4.
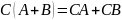 .
.
Транспонированием
матрицы
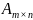 называется операция замены строк матрицы
столбцами с теми же номерами. В результате
получается новая матрица
называется операция замены строк матрицы
столбцами с теми же номерами. В результате
получается новая матрица
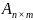 порядка
порядка
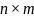 с
теми же элементами, что и матрица
.
Операцию транспонирования матрицы
обозначают
с
теми же элементами, что и матрица
.
Операцию транспонирования матрицы
обозначают
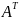 .
Например, если
.
Например, если
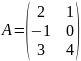 ,
то
,
то
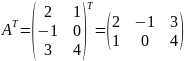 .
.
Относительно операции транспонирования имеют место следующие свойства:
1.
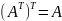
2.
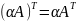
3.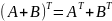
4.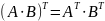 .
.
Кроме указанных операций с матрицами можно указать еще одну операцию, которую называют обращением матрицы или нахождение матрицы, обратной данной. Для того чтобы ввести эту операцию, необходимо рассмотреть понятие определителя матрицы.
