5. Порівняння інтеграла Лебега з інтегралом Рімана.

Теорема:Якщо існує інтеграл Рімана , то функція інтегрована на по Лебегу і .

Твердження. Обмежена на множині Е функція інтегрована на Е.

1. Легко навести приклади обмежених функцій на деякому відрізку, інтегрованих по Лебегу, але не інтегрованих по Ріману. Наприклад, функція Діріхлє на відрізку , що дорівнює 1 для раціональних і 0 для ірраціональних;

2) Необмежені функції взагалі не можуть бути інтегрованими по Ріману (не враховуючи невласні інтеграли, але багато з них є інтегрованими по Лебегу). Конкретно, будь-яка функція , для якої інтеграл Рімана існує при кожному та має кінцеву границю. І при , інтегруєма по Лебегу на , при чому .

3) Невласний інтеграл: 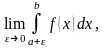у випадку ,коли 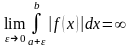, не існує в значенні Лебега, оскільки згідно властивості 5 і повинні бути сумованими одночасно. Наприклад , існує як (умовно збіжний) невласний інтеграл Рімана, але не існує як інтеграл Лебега.

4) Якщо розглядається функція f(x) на всій прямій, то інтеграл Рімана існує для f(x) у невласному значенні. Якщо такий інтеграл збігається абсолютно, то власний інтеграл Лебега існує і має те ж саме значення. Якщо ж інтеграл збігається лише умовно, то в лебеговому значенні функція не інтегрована. Наприклад функція не інтегрована по Лебегу на всій прямій, так як 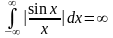. Однак невласний інтеграл .

6. Міра і інтеграл Лебега в .

Як і в одномірному випадку, в визначаються внутрішня та зовнішня міри обмеженої множини, вимерність і міра множини, вимірюємі функції і ми приходимо до кратного інтеграла Лебега.

Контрольні питання і завдання.

1. Яка множина зветься компактною?

2. Чому компактна множина замкнена? Доведіть.

3. Яка числова функція називається мірою?

4. Якими властивостями володіє абстрактна міра?

5. Яка дійсна функція називається вимірною?

6. Яка послідовність функцій , визначених на деякій множині 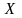із заданою на ній мірою, називається збіжною майже скрізь(всюди) до функції ?

7. Яка послідовність вимірних на функцій називається збіжною за мірою до вимірної функції f(x)?

8. Який зв’язок існує між збіжністю майже всюди і збіжністю за мірою?

9. Сформулюйте теорему Риса про зв’язок між збіжністю за мірою і збіжністю майже всюди.

10. Дайте означення інтеграла Лебега.

11. Наведіть властивості інтеграла Лебега.

12. Як визначається інтеграл Лебега на числовій прямій.

13. Яка функція називається функцією із сумованим раціональним степенем p, де p 1?

14. . Як визначається простір функцій, що інтегруються з показником степеня p, де p 1?