МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

Лекція 16

Тема: " Міра, інтеграл Лебега та його властивості. Порівняння інтегралів Рімана та Лебега".

Дисципліна : "Функціональний аналіз"

Викладач Гусарова І. Г.

Харків,2013

Тема: Міра, інтеграл Лебега та його властивості. Порівняння інтегралів Рімана та Лебега

1. Абстрактна міра та інтеграл.

Нехай Х – множина елементів деякої природи. Сукупність підмножин множини Х називається 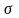- алгеброю, якщо виконуються наступні умови:

1. X

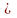
2. із 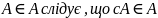(cA доповнення: X\A);

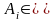
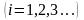3. якщо , то .

Із умов 1) – 3) відразу випливає, що 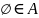і перетин кінцевого або зліченого числа множин, які лежать в - алгебрі, теж лежать в - алгебрі (якщо 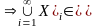, тобто , тобто .

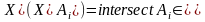Приклади:

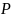
1. Сукупність (або - булеан) усіх підмножин множини Х є прикладом - алгебри.

2. Борелівські множини на фіксованому відрізку числової прямої є -алгеброю. Дійсно, сукупність множин, яка може бути отримана із відкритих і замкнених множин методом операції об’єднання та перетину, повторюваних у будь-якому порядку скінчене або злічене число разів утворює борелівську систему В множин на відрізку .

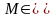
Якщо 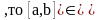B, , якщо 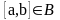, так як булеан є -алгеброю.

Означення: Множину, яка належить - алгебрі , будемо називати -вимірною (або просто вимірною)

Означення: Числова функція 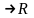називається мірою, якщо

1)

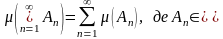
2) при

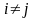
Теорема1: Міра є монотонною функцією, тобто:

1. ;

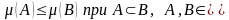2. ( ) ;

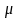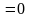3. ;

4. якщо .

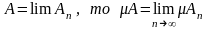Означення: Нагадаємо, що послідовність множин називається збіжною до множини А, якщо

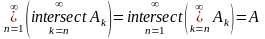
Означення: Дійсна функція 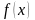, визначена на 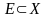називається вимірною, якщо можна виміряти множину Е і прибудь-якому дійсному с, можна виміряти множину .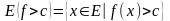

Теорема 2: Для вимірності А на вимірній множині Е необхідно і достатньо вимірності при кожному одної з трьох множин: .

Означення: Послідовність функцій 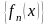, визначених на деякій множині Х із заданою на ній мірою, називається збіжною майже скрізь(всюди) до функції , якщо

(1)

майже для всіх х є Х (тобто множина всіх точок х, в яких (1) не виконується, має міру нуль).

Приклад:

Послідовність функцій , визначених на відрізку , при 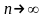збігається до функції майже скрізь(а саме окрім точки х=1).

Твердження: Клас вимірних функцій замкнений відносно алгебраїчних операцій 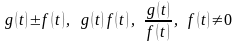- вимірні, якщо 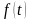, вимірні і відносно граничного переходу, навіть якщо збіжність розуміється як збіжність майже скрізь, тобто з точністю до множини з мірою, яка дорівнює нуль.

Теорема 3 (Д.П.Єгорова):Якщо 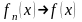майже скрізь на Е, то для будь-якого 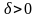можна знайти вимірну підмножину 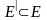таку, що 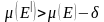і на 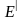послідовність збігається до f(x) рівномірно.

Означення: Послідовність вимірних на Е збігаються за мірою до вимірної функції f(x), якщо для будь-якого ,

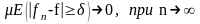
Твердження: Якщо послідовність збігається до f(x) майже всюди, то вона збігається до f(x) і за мірою.

Обернене твердження не вірне, але вірна наступна теорема.

Теорема4 ( Ріса ):Нехай послідовність вимірних функцій збігається за мірою до f(x). Тоді із цієї послідовності можемо обрати підпослідовність , яка збігається до f(x) майже скрізь.

Нехай Е – вимірна множина та f(x) - невід’ємна вимірна на Е функція .

Розіб’ємо Е на скінчене число вимірних частин 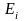, які не перетинаються:

(2)

і нехай складемо

(3)

Означення: Скінчена, або нескінчена верхня межа таких сум (3) по різним розбиттям вказаного виду(2) називається інтегралом Лебега від f(x) на множині Е і позначаються .

Означення: Якщо 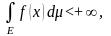то невід’ємна функція f(x) називається інтегрованої( сумованою ) на множині Е.

Для функції f(x), яка приймає на множині Е значення різних знаків , вважаємо (за визначенням): , де 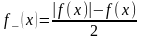, , 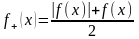якщо хоч один з інтегралів справа є скінченним.

Означення. Якщо , то функція f(x) називається інтегрованої (сумованою) на множині Е.