
- •Лекція 1 Вступ до кінематики
- •Способи завдання руху точки
- •Швидкість точки
- •Завдання для самостійної роботи студентів
- •Лекція 2 Прискорення точки
- •Осі натурального тригранника
- •Формули рівномірного і рівнозмінного руху точки
- •Завдання до самостійної роботи студентів
- •Лекція 3 Поступальний рух твердого тіла
- •Обертальний рух твердого тіла навколо нерухомої осі
- •Часткові випадки
- •Швидкості і прискорення точок обертального тіла в скалярному вигляді
- •Швидкості та прискорення точок обертального тіла у векторному вигляді
- •Завдання до самостійної роботи студентів
- •Рух твердого тіла навколо нерухомої точки
- •Швидкості та прискорення точок тіла
- •Способи визначення кутової швидкості і кутового прискорення твердого тіла з одною нерухомою точкою
- •Завдання до самостійної роботи студентів
- •Складний рух точки
- •Теорема про складання швидкостей
- •Теорема Коріоліса
- •Наслідки теореми Коріоліса
- •Правило м.Є. Жуковського
- •Завдання до самостійної роботи студентів
- •Лекція 6 Плоскопаралельний рух твердого тіла
- •Визначення швидкостей точок тіла
- •Теорема про проекції швидкостей двох точок
- •Миттєвий центр швидкостей
- •Визначення прискорень точок тіла
- •Завдання до самостійної роботи студентів
- •Література
Визначення швидкостей точок тіла
На основі
рівнянь (6.1) можна, користуючись формулами
(1.9), (1.10), (3.4), (3.6), обчислити для будь-якої
миті руху величину і напрям швидкості
![]() полюсу А
та кутової швидкості .
полюсу А
та кутової швидкості .
Т оді,
розглядаючи рух деякої точки В
як складний і враховуючи (5.3), маємо:
оді,
розглядаючи рух деякої точки В
як складний і враховуючи (5.3), маємо:
![]() ,
(6.2)
,
(6.2)
де
![]() - переносна швидкість поступального
руху разом з т. А;
- переносна швидкість поступального
руху разом з т. А;
![]() - швидкість
відносного руху при обертанні точки В
навколо полюса А,
причому
- швидкість
відносного руху при обертанні точки В
навколо полюса А,
причому
![]() .
.
Рівняння (6.2) відображає наступну теорему: швидкість будь-якої точки плоскої фігури уявляє собою векторну суму швидкості поступального руху разом з полюсом А і швидкості обертального руху даної точки навколо цього полюса.
Теорема про проекції швидкостей двох точок
Проекції швидкостей двох будь-яких точок плоскої фігури на пряму, що з’єднує ці точки, дорівнюють одна одній.
Доведення цієї теореми очевидне, якщо спроектувати векторне рівняння (6.2) на пряму АВ:
![]() ,
,
де
![]() ,
оскільки
,
оскільки
![]() ,
і, таким чином, маємо:
,
і, таким чином, маємо:
![]() . (6.3)
. (6.3)
Миттєвий центр швидкостей

При плоскопаралельному русі завжди існує така точка плоскої фігури, швидкість якої у дану мить дорівнює нулеві. Ця точка називається миттєвим центром швидкостей.
Проведемо через т. А перпендикуляр до і оберемо т. Р на відстані
![]() .
.
Доведемо,
що
![]() .
.
Згідно з (6.2)
![]() ,
,
де
![]() ,
причому
,
причому
![]() ,
тобто
,
тобто
![]() ,
і
.
,
і
.
Якщо при визначенні швидкості будь-якої точки обирати за полюс т. Р, то згідно (6.2) будемо мати
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,
або,
враховуючи
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,
причому
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Звідси виникає важливе для вирішення практичних задач співвідношення:
![]() . (6.4)
. (6.4)
Відстань будь-якої точки до миттєвого центра швидкостей називають миттєвим радіусом. Тому, враховуючи (6.4), нескінченно мале переміщення плоскої фігури можна уявити як миттєве обертання навколо миттєвого центра швидкостей, а через те швидкість точок плоскої фігури перпендикулярна до їх миттєвих радіусів.
Далі наведемо такі способи визначення положення миттєвого центра швидкостей.
М
 иттєвий
центр швидкостей уявляє собою точку
перетину перпендикулярів до векторів
швидкостей усіх точок плоскої фігури,
проведених через дані точки.
иттєвий
центр швидкостей уявляє собою точку
перетину перпендикулярів до векторів
швидкостей усіх точок плоскої фігури,
проведених через дані точки.
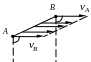
Я
 кщо
вектори швидкостей
і
кщо
вектори швидкостей
і
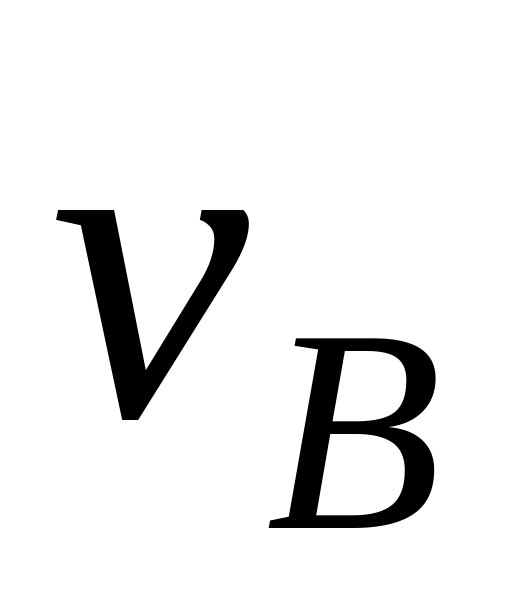 точок А
і В
паралельні, а
точок А
і В
паралельні, а
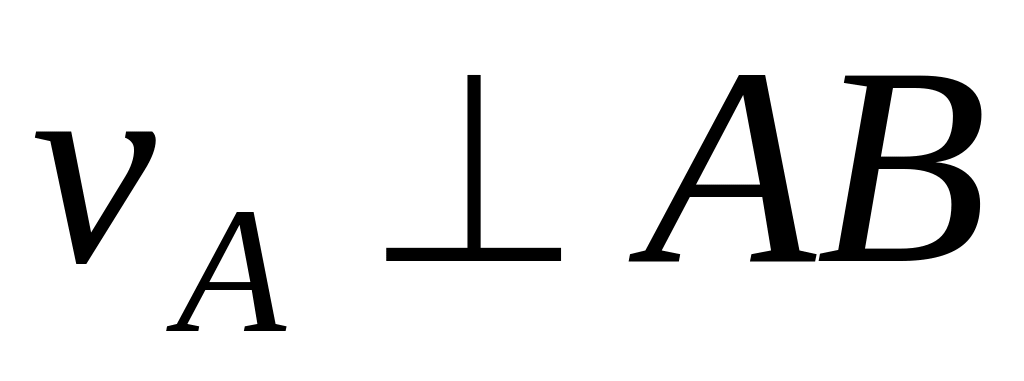 ,
то для визначення миттєвого центра
швидкостей треба врахувати пропорційність
величин швидкостей точок їх миттєвим
радіусам.
,
то для визначення миттєвого центра
швидкостей треба врахувати пропорційність
величин швидкостей точок їх миттєвим
радіусам.Я
 кщо
вектори швидкостей
і
паралельні, але не перпендикулярні АВ,
то миттєвий центр швидкостей знаходиться
в нескінченності, тобто тіло бере участь
у миттєво поступальному русі, при якому
швидкості всіх точок в дану мить рівні
між собою, а
кщо
вектори швидкостей
і
паралельні, але не перпендикулярні АВ,
то миттєвий центр швидкостей знаходиться
в нескінченності, тобто тіло бере участь
у миттєво поступальному русі, при якому
швидкості всіх точок в дану мить рівні
між собою, а
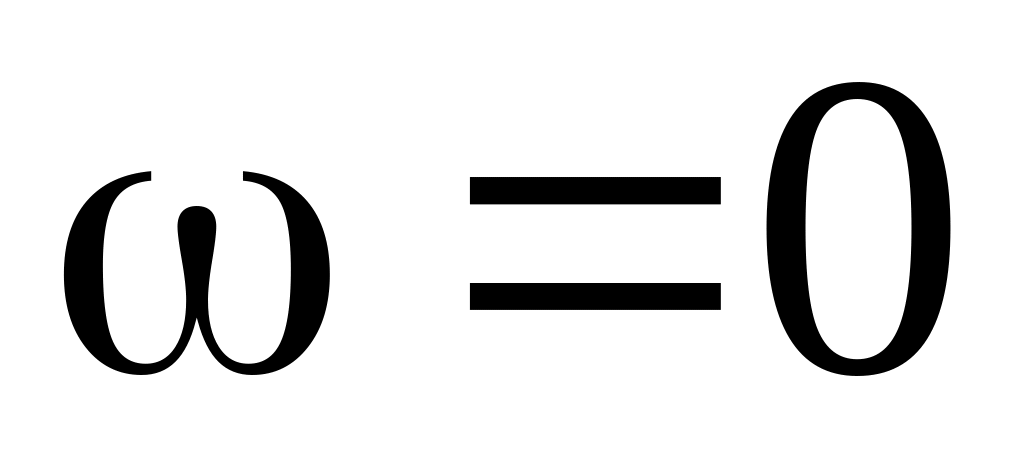 .
.
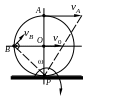
При плоскопаралельному русі тіла, що здійснюється його коченням по нерухомій поверхні без ковзання миттєвим центром швидкостей буде в кожну мить точка дотику.
Визначення прискорень точок тіла
Застосовуючи послідовність міркувань аналогічну використаній в теоремі про складання швидкостей (6.2), можна на основі теореми Коріоліса про складання прискорень точки при поступальному переносному русі записати:
![]() , (6.5)
, (6.5)
д е
прискорення т. А
є для т. В
переносним, а прискорення
е
прискорення т. А
є для т. В
переносним, а прискорення
![]() - відносним, тобто тим прискоренням, що
буде мати т. В
при обертанні навколо т. А
- відносним, тобто тим прискоренням, що
буде мати т. В
при обертанні навколо т. А
![]() ,
(6.6)
,
(6.6)
причому
![]() ,
,
![]() . (6.7)
. (6.7)
Якщо
прийняти до уваги, що в загальному
випадку
![]() ,
то, враховуючи (6.6), рівняння (6.5) має такий
остаточний вигляд:
,
то, враховуючи (6.6), рівняння (6.5) має такий
остаточний вигляд:
![]() . (6.8)
. (6.8)
При
розв’язанні практичних задач будувати
вектор
![]() згідно (6.8) нерідко є недоречним. Зручніше
обчислити модуль і напрям вектора
,
спроектувавши векторне рівняння (6.8) на
обрані осі координат аналогічно (2.3),
(2.4).
згідно (6.8) нерідко є недоречним. Зручніше
обчислити модуль і напрям вектора
,
спроектувавши векторне рівняння (6.8) на
обрані осі координат аналогічно (2.3),
(2.4).
