Завдання до самостійної роботи студентів

Проробити параграфи рекомендованої літератури:

[1] Розділ ІІ, введення, глава 1 §§ 2, 4, 5

[2] Розділ ІІ, глава ІХ §§ 39, 40-44

[3] Розділ ІІ, глава ІХ §§ 70-76

Відповісти на питання:

1. Чому дорівнює вектор прискорення точки?

2. Як визначається величина і напрям прискорення точки при координатному способі завдання руху?

3. Які осі називають осями натурального тригранника?

4. Що характеризують дотичне і нормальне прискорення та як визначають їх величину і напрям?

Вирішити задачі:

[4] №№ 12.7, 12.18, 12.22

Лекція 3 Поступальний рух твердого тіла

Поступальним називається такий рух твердого тіла, при якому пряма, проведена через будь які дві точки тіла, залишається паралельною початковому положенню.

В ластивості поступального руху визначаються наступною теоремою: при поступальному русі усі точки тіла описують однакові (при накладанні співпадаючі) траєкторії та мають в кожну мить однакові по модулю і за напрямом швидкості та прискорення.

Для будь-яких точок А і В маємо

, де .

Тоді

,

або

. (3.1)

Після диференціювання (3.1) отримаємо

,

або

. (3.2)

Через довільність вибору точок А і В можна стверджувати, що рівності (3.1) і (3.2) справедливі для всіх точок тіла. Тому для цього випадку доречними є поняття швидкості тіла та прискорення тіла.

Обертальний рух твердого тіла навколо нерухомої осі

О бертальним називають такий рух твердого тіла, при якому всі точки, котрі належать деякій прямій, що незмінно пов’язана з тілом, залишаються нерухомими в даній системі відліку. Ця пряма називається віссю обертання.

Переміщання обертального тіла з одного положення в інше називається поворотом.

Кут  між проведеними через вісь обертання півплощинами (нерухома І і рухома разом з тілом ІІ) називають кутом повороту тіла.

Таким чином, закон обертального руху твердого тіла навколо нерухомої осі Аz має вигляд

. (3.3)

Основними кінематичними характеристиками обертального руху тіла є кутова швидкість  і кутове прискорення .

За проміжок часу кут повороту зміниться на . Тоді середня кутова швидкість

,

а миттєва кутова швидкість

. (3.4)

Розмірність .

Мірою зміни кутової швидкості є кутове прискорення. Міркуючи аналогічно попередньому, середня величина кутового прискорення

,

а миттєве кутове прискорення

.

Розмірність . Із врахуванням (3.4) остаточно можна записати

. (3.5)

Вектори кутової швидкості і кутового прискорення спрямовують вздовж нерухомої осі Аz (точка прикладання не має значення). При цьому вектор кутової швидкості спрямовують в напрямку, з якого обертання тіла спостерігається проти ходу стрілки годинника, тобто

(3.6)

і, якщо , то , а, якщо , то .

Аналогічно

(3.7)

і, якщо , то , а, якщо , то .

Часткові випадки

1. Рівномірне обертання тіла

, ,

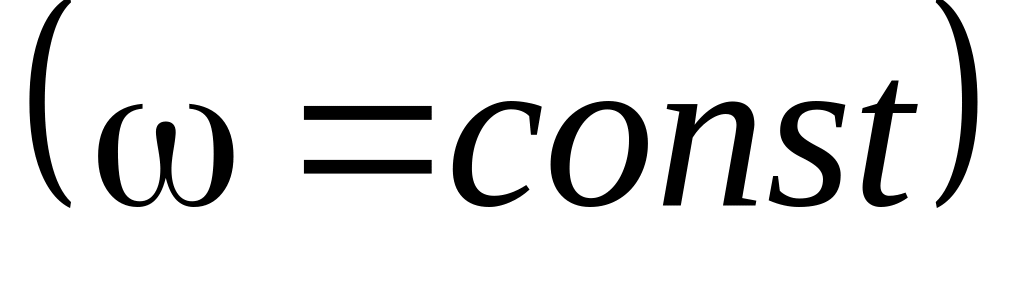
тобто

. (3.8)

2. Рівнозмінне обертання тіла

, ,

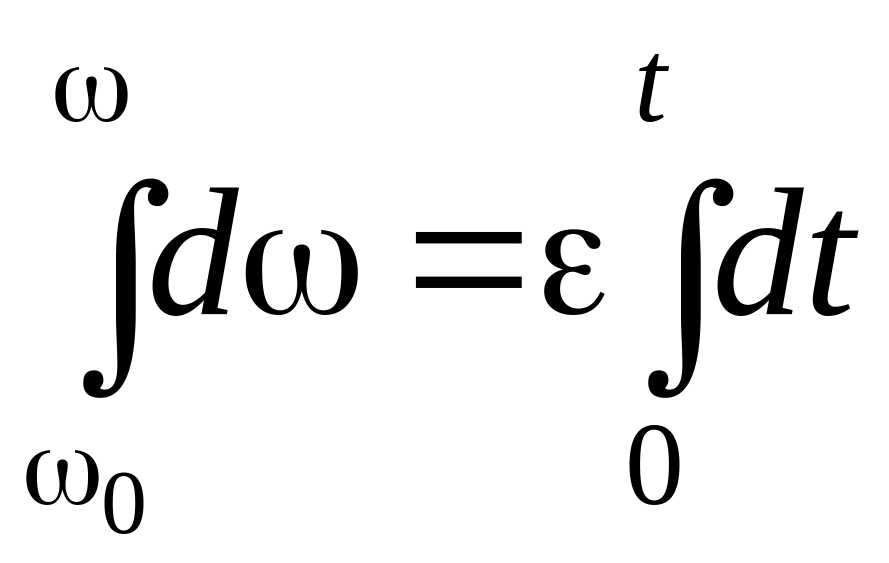тобто

. (3.9)

Якщо врахувати (3.4) в (3.9), то маємо

,

і остаточно

. (3.10)