2

М ІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

КОНСПЕКТ ЛЕКЦІЙ

з теоретичної механіки

Частина ІІ. КІНЕМАТИКА

Під загальною редакцією проф. В.Б. Малєєва

Розглянуто на засіданні

кафедри теоретичної механіки

протокол №2 від 01.10.2008 р.

Затверджено на засіданні

навчально-методичної ради

ДонНТУ протокол №6

від 15.12.2008 р.

Донецьк - 2008

УДК 531

Лекції з теоретичної механіки (частина ІІ. Кінематика): навчальний посібник для студентів всіх спеціальностей і форм навчання технічних вузів / Л.О. Степанова, А.П. Стегнієнко. – Донецьк: ДонНТУ, 2008. – 30 с., іл.

Лекції містять в лаконічній і доступній формі зміст другої частини курсу теоретичної механіки (кінематика).

Призначається як навчальний посібник для студентів всіх спеціальностей технічних вузів денної і заочної форм навчання, а також для організації самостійної роботи студентів.

Укладачі: доц. Степанова Л.О.

доц. Стегнієнко А.П.

Рецензент: проф. Скоринін М.Й.

Лекція 1 Вступ до кінематики

Кінематикою називається розділ механіки, в якому вивчається рух матеріальних об’єктів без врахування їх інертності та діючих на них сил.

Рух матеріальних тіл у просторі здійснюється за спливанням часу. Простір розглядається як тривиміровий простір, час як універсальний, тобто спливаючий однаково у всіх системах відліку. У всіх задачах кінематики час (t) уявляє незалежну змінну, всі інші змінні є функції часу.

Оскільки під рухом тіла розуміють зміну із спливанням часу його положення відносно інших тіл, то з тілом, відносно якого вивчається рух, пов’язують яку-небудь систему координат, що утворює з цим тілом систему відліку.

При розгляданні руху точок або тіл одночасно до декількох систем відліку основною системою вважається та із цих систем, відносно якої визначається рух усіх інших.

Щоб досліджувати рух точки або тіла, його треба задати (математично описати).

Задати рух точки або тіла – це означає вказати спосіб, за допомогою якого можна визначити положення точки або тіла відносно вибраної системи відліку у любий момент часу.

Спосіб завдання руху називають законом (рівнянням) руху.

Основна задача кінематики точки і твердого тіла полягає в тому, щоб знаючи закон руху точки (тіла) встановити методи визначення усіх кінематичних величин (траєкторії, швидкості, прискорення та ін.), що характеризують цей рух.

Неперервна лінія, котру описує рухома точка відносно даної системи відліку називається траєкторією точки. По виду цієї лінії розрізняють прямолінійний або криволінійний рух точки.

Способи завдання руху точки

1. Векторний спосіб

П ри цьому способі треба знати радіус-вектор рухомої точки М, що проводиться до неї з будь-якого заданого або вибраного полюсу О. Звідси закон руху

(1.1)

Г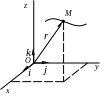 еометричне місце кінців вектора , тобто годограф цього вектора, визначає траєкторію рухомої точки.

2. Координатний спосіб.

Положення рухомої точки М визначають декартовими координатами. Тому закон руху має вигляд:

. (1.2)

Якщо прийняти до уваги орти декартової системи відліку, то неважко переконатись у зв’язку цього способа з векторним:

. (1.3)

При координатному способі можна отримати рівняння траєкторії руху точки, виключаючи із закону руху параметр t.

П риклад: .

Звідси траєкторією точки буде еліпс, рівняння якого має вигляд

.

3. Натуральний спосіб

Щ об задати рух точки натуральним способом, треба:

а) задати траєкторію точки;

б) вибрати початок відліку на траєкторії (т. О) із зазначенням додатного та від’ємного напряму відліку дугової (криволінійної) координати S;

в) задати закон руху точки вздовж траєкторії у вигляді:

. (1.4)

Примітка: не плутати величину координати S з пройденим точкою шляхом.

Швидкість точки

Ш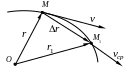 видкістю точки називається кінематична міра руху точки, яка дорівнює похідній за часом від радіуса-вектора цієї точки у даній системі відліку.

,

,

,

.

Таким чином,

. (1.5)

Розмірність швидкості

[v] = м/с.

Швидкість точки при координатному способі завдання руху, враховуючи (1.3) у (1.5), визначається формулами:

, (1.6)

оскільки .

З іншого боку

. (1.7)

Порівнюючи (1.6) і (1.7) , робимо висновок, що проекції вектора швидкості на декартові осі координат визначаються таким чином:

; ; . (1.8)

Тоді

; (1.9)

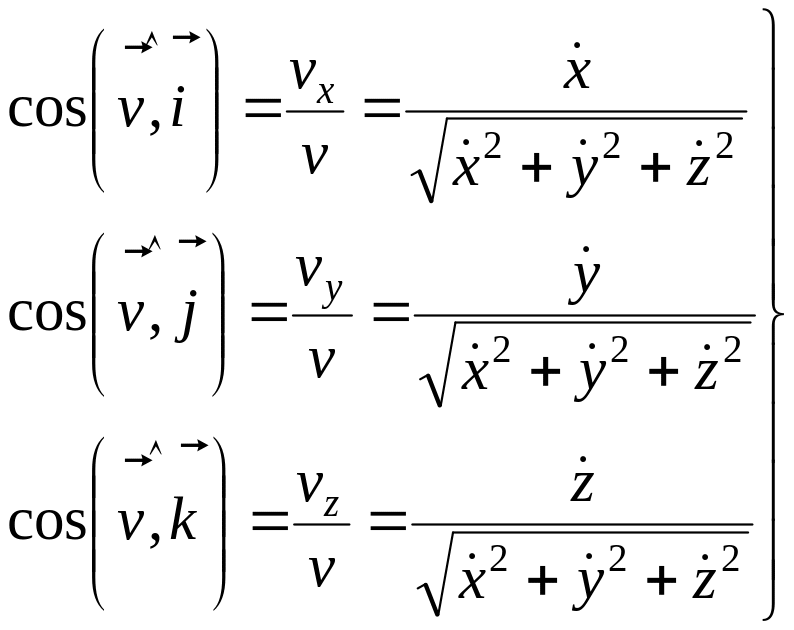. (1.10)

Швидкість точки при натуральному способі завдання руху:

,

,

,

.

Таким чином,

. (1.11)