§2. Некоторые сведения о комплексных числах и многочленах

2.1. Поле комплексных чисел. Алгебраическая форма записи комплексного числа.

Рассмотрим множество , элементами которого являются пары , где . Введём в этом множестве арифметические действия.

Действие сложение между элементами и

о пределяется следующим образом: и обладает свойствами:

1. ассоциативность ;

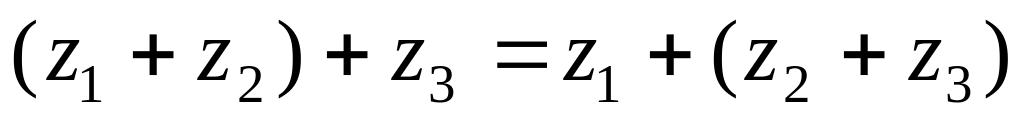2. существование нулевого элемента ;

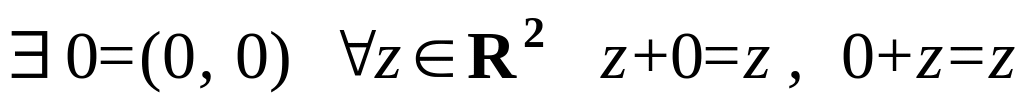3. существование противоположного элемента ;

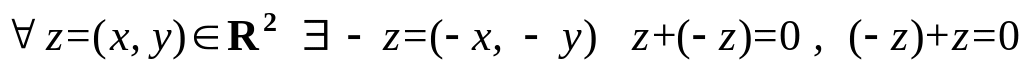4. коммутативность .

Действие умножение между элементами и

определяется следующим образом и обладает свойствами:

1. ассоциативность ;

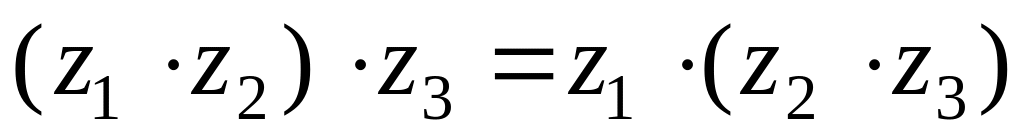2) существование единичного элемента

;

3) существование обратного элемента ;

4. коммутативность .

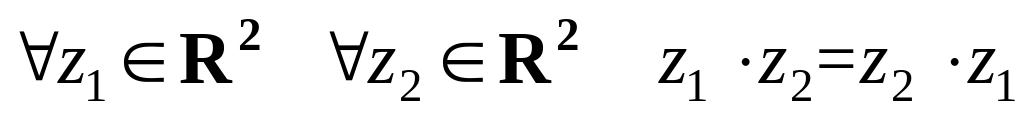Имеет место также свойство дистрибутивности

.

Комплексное число можно изображать либо точкой на плоскости, либо вектором. Если ввести для единичных векторов обозначения и , а также если учесть, что , то любое комплексное число можно записать в виде:

- алгебраическая форма записи комплексного числа.

При этом действительное число x называется действительной частью комплексного числа z и обозначается x = Re z, а действительное число y называется мнимой частью комплексного числа z и обозначается y = Im z .

Заметим, что . Тогда умножение комплексных чисел в алгебраической форме можно производить, просто раскрывая скобки:

Комплексное число называется

сопряженным числом к числу .

Действие деление между элементами

и определяется следующим образом:

Свойства сопряжённых чисел

1) ;

2) ;

3) .

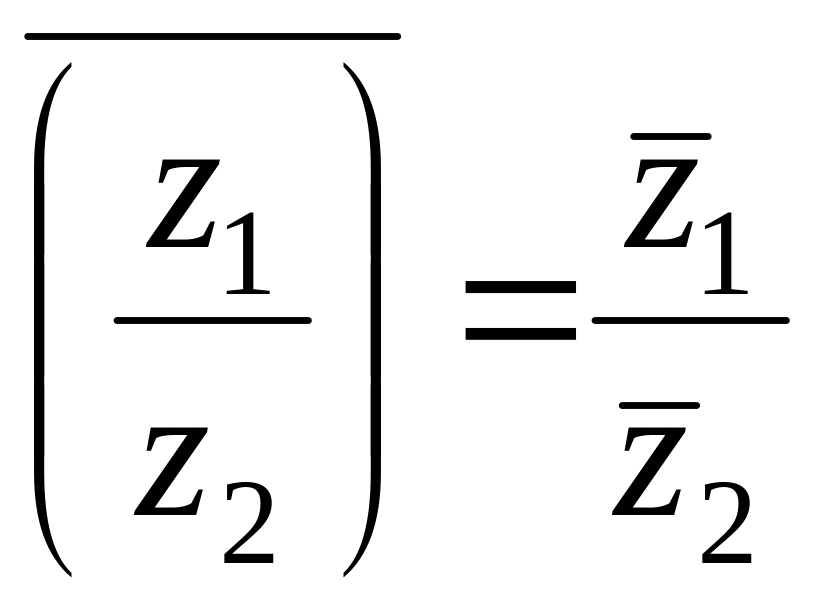
2.2. Модуль и аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.

Для любого комплексного числа можно определить его модуль по формуле: .

Г еометрический смысл модуля: модуль – это расстояние между началом координат и точкой , соответствующей числу .

Свойства модуля:

1) ;

2) ;

3) – неравенство треугольника;

4) – обратное неравенство треугольника.

Определение. Аргументом комплексного числа называется угол, между положительным направлением оси OX и радиус-вектором числа z.

– главное значение аргумента, этот угол изменяется в промежутке . Он вычисляется по формуле

Произвольный угол, соответствующий данному комплексному числу, принадлежит множеству .

Заметив, что и , и подставив эти выражения

в алгебраическую форму записи комплексного числа, получим тригонометрическую форму записи комплексного числа

Пример1. Записать комплексное число в тригонометрической форме .

Действительная и мнимая части этого числа равны соответственно

, . Найдем модуль .

Так как мнимая часть отрицательна, то аргумент находится по формуле

Получаем тригонометрическую форму записи:

.

В тригонометрической форме записи удобно выполнять действия : умножение, деление, возведение в степень и извлечение корня.

Чтобы умножить два комплексных числа и

в тригонометрической форме записи, нужно их модули перемножить, а аргументы сложить: .

Доказательство.

Чтобы поделить два комплексных числа и в тригонометрической форме записи, нужно их модули поделить, а аргументы вычесть.

.

.