Контрольная работа по дисциплине «Макроэкономическое планирование и прогнозирование» состоит из:
Теоретического вопроса
Задачи на тему «Расчет ИРЧП»
Задачи на тему «Прогнозирование макроэкономических показателей».
1. Варианты задач и перечень теоретических вопросов
№ вар. |
Ф.И.О. |
группа |
Теоретический вопрос |
1 |
Белый Р.Н. |
ИВЭ21 |
Методы изучения национальной экономики |
Аюбов Т.Н. |
ИВЭ22 |
||
2 |
Вострикова Е.С. |
ИВЭ21 |
Структура модели национальной экономики, основные ее составляющие |
Верховский С.В. |
ИВЭ22 |
||
3 |
Губа Т.С. |
ИВЭ21 |
Моделирование равновесного состояния рыночного хозяйства |
Другалева Н.Г. |
ИВЭ22 |
||
4 |
Комар Д.А. |
ИВЭ21 |
Прогнозирование трудовых ресурсов и их использования
|
Карасаев М.А. |
ИВЭ22 |
||
5 |
Луговкина Е.А. |
ИВЭ21 |
Индикативное макроэкономическое планирование |
Костин Н.Ю. |
ИВЭ22 |
||
6 |
Немчин Г.А. |
ИВЭ21 |
Кривая А. Филипса и ее использование в стабилизации экономики |
Кущев А.С. |
ИВЭ22 |
||
7 |
Паламарь Д.С. |
ИВЭ21 |
Модели неравномерности в распределении доходов. Кривая М. Лоренца |
Назарова А.А. |
ИВЭ22 |
||
8 |
Полуэктов П.А. |
ИВЭ21 |
Модели денежного обращения |
Рыжкова А.А. |
ИВЭ22 |
||
9 |
Расцветаев А.Л. |
ИВЭ21 |
Модели сбережений и доходов населения |
Слащева Е.А. |
ИВЭ22 |
||
10 |
Свиакаури А.Х. |
ИВЭ21 |
Концепции долгосрочного социального экономического развития России. Стратегические и тактические приоритеты |
Сова М.А. |
ИВЭ22 |
||
11 |
Свиридова М.В. |
ИВЭ21 |
Система национальных счетов (СНС) и методы расчета ВНП |
Хаибашева Е.В. |
ИВЭ22 |
||
12 |
Силич А.А. |
ИВЭ21 |
Прогнозирование и планирование потребительского рынка |
|
ИВЭ22 |
||
13 |
Хохлов Н.А. |
ИВЭ21 |
Прогнозирование и регулирование оплаты труда. Баланс денежных доходов и расходов населения |
|
ИВЭ22 |
||
14 |
Хохлова Н.Е. |
ИВЭ21 |
Планирование занятости. Сводный баланс трудовых ресурсов |
|
ИВЭ22 |
Задача на тему «Расчет ирчп»
Определить ИРЧП (по данным 20** года). При выполнении задания расчет привести полностью.
(пример расчета приведен в лекциях)
№ вар. |
Город, регион, область |
ВВП на душу населения, долл.США |
Индекс дохода |
Средняя ожидаемая продолжительность жизни |
Грамотность, % |
Доля учащихся, % |
1 |
Тюменская область |
49969 |
1,000 |
68,57 |
99,2 |
71,7 |
2 |
Санкт-Петербург |
16817 |
0,855 |
69,86 |
99,8 |
98,8 |
3 |
Сахалинская область |
26657 |
0,932 |
64,48 |
99,4 |
66,9 |
4 |
Челябинская область |
13664 |
0,821 |
67,14 |
99,1 |
75,2 |
5 |
Свердловская область |
14190 |
0,827 |
67,5 |
99,2 |
72 |
6 |
Ростовская обл. |
8288 |
0.737 |
68.38 |
99,1 |
72,7 |
7 |
Волгоградская обл. |
10178 |
0.772 |
68.84 |
98,9 |
70,1 |
8 |
Липецкая обл. |
15373 |
0.840 |
67.31 |
98,4 |
68,3 |
9 |
Краснодарский край |
10003 |
0.769 |
69.25 |
99,0 |
67,6 |
10 |
Респ. Татарстан |
18080 |
0.867 |
69.44 |
99,0 |
75,6 |
11 |
Белгородская обл. |
13738 |
0.822 |
70.33 |
98,6 |
73,4 |
12 |
Респ. Саха (Якутия) |
13629 |
0.820 |
66.17 |
99,0 |
75,4 |
13 |
Мурманская обл. |
13032 |
0.813 |
66.72 |
99,6 |
65,1 |
14 |
Ярославская обл. |
11745 |
0.795 |
67 |
99,2 |
73,5 |
3. Тема «Прогнозирование макроэкономических показателей».
Экономическое прогнозирование. Прогнозирование развития с помощью моделей кривых роста. Анализ тренда
Для экономического прогнозирования с помощью одномерных временных рядов удобно использовать кривые роста, которые позволяют получить выравненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой.
При экономическом прогнозировании с использованием кривых роста необходимо:
1) выбрать одну или несколько кривых, форма которых соответствует характеру изменения временного ряда;
2) оценить параметры выбранных кривых;
3) проверить адекватность выбранных кривых прогнозируемому процессу и окончательно выбрать кривую роста;
4) сделать точечный и интервальный прогноз.
Для выравнивания экономических временных рядов могут быть применены следующие типы кривых роста:
I тип. Функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста. Эти условия справедливы для многих экономических показателей (рис.1а, 1б).
II тип. Кривые, описывающие процесс, имеющий предел роста в исследуемом периоде. (среднедушевое потребление продуктов питания, расход удобрений на единицу площади и т.д.). Такие функции называются кривыми насыщения, а если они имеют точку перегиба – то они относятся к S-образным кривым (рис.1в).
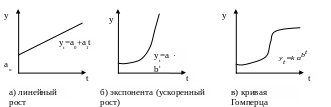
Рис.1
Среди кривых I типа следует выделить класс полиномов:
,
где ai (i=0, 1, …, p) – параметры многочлена;
t – независимая переменная (время).
Полином первой степени yt=a0+a1t на графике изображается прямой и используется для описания процессов, развивающихся во времени равномерно (рис.1а). Оценка параметров a0 и a1 в данной модели производится методом наименьших квадратов, что позволяет получить следующие выражения:
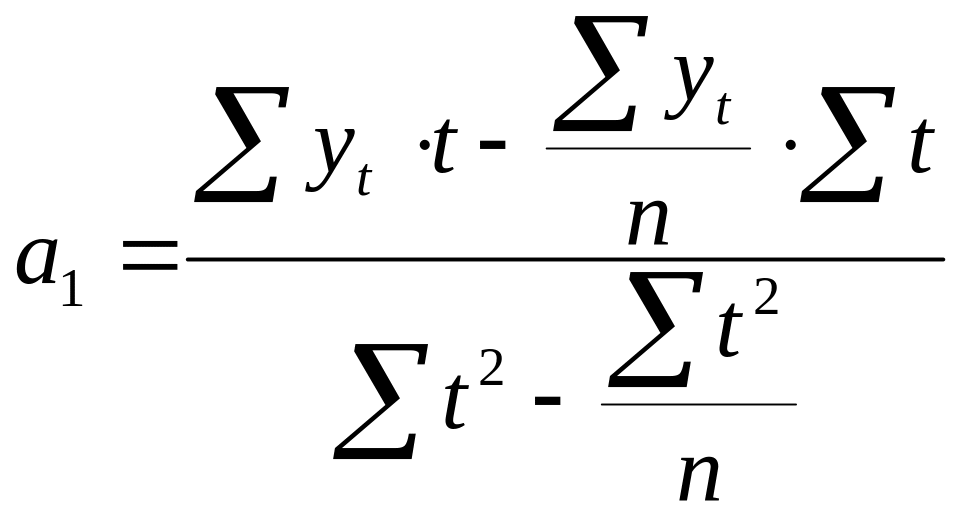
Для упрощения расчетов перенесем начало координат в середину ряда динамики. Если до переноса координат t было равно 1, 2, 3, …, то после переноса:
- для четного числа членов ряда t = …, -5; -3; -1; 1; 3; 5; …;
- для нечетного числа членов ряда t = …, -3; -2; -1; 0; 1; 2; ; … .
Такой подход упрощает процесс нахождения параметров. Оценки параметров имеют вид:
