Данный курс представляет собой учебно-методический комплекс, рассчитанный на студентов 1-ого курса магистратуры по специальности «Инженерно-физические технологии в наноиндустрии», направление подготовки: 222900 «Нанотехнологии и микросистемная техника» и адаптирован для инженерных специальностей. Наряду со ставшими классическими и хорошо освещенными в литературе и других курсах темами [1. Гуртов В. А., Осауленко Р. Н.:Физика твердого тела для инженеров: учебное пособие. 2-е изд., исправ. и доп. Гриф УМО вузов России. 2012. Издательство: Техносфера. С 520, ISBN: 9785948363271; 2. Б.Е. Винтайкин Физика твердого тела. МГТУ им. Н.Э. Баумана. Физика в техническом университете 6 том под ред. Л.К. Мартинсона, Н.А. Морозова, 2001-2002 http://fn.bmstu.ru/data-physics/library/physbook/tom6/front.html; 3. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. В 10-ти т. Т. IX. Теория конденсированного состояния: Учеб. пособие. — 4-е изд., испр. и доп. — М.; Наука. Гл. ред. физ.-мат. лит., 1987. — 448 с. Добавить ] добавлено краткое рассмотрение некоторых аспектов взаимодействия твердого тела с плазмой, пучками ионов или лазерным излучением. Поскольку в соответствии с распоряжением № только 20% приходится на лекции, то некоторые методически важные темы представлены в виде задач для решения на семинарах. Кроме того, некоторые интересные с точки зрения составителя вопросы вынесены на самостоятельное изучение студентам с отчетом в виде презентации и выступления на семинаре. Таким образом, курс состоит из следующих частей:

1. Лекции

2. Тестовые задания

3. Семинары – решения задач

4. Семинары – выступления студентов с рефератами

5. Контрольные (2 в середине и в конце)

Лекция 1. Типы конденсированных сред. Наиболее энергетически выгодное состояние макроскопической системы взаимодействующих частиц.

Аннотация.

В данном разделе приведена классификация конденсированных сред, условно поделенных на 5 типов с отдельным выделением стёкол и жидких кристаллов, т.е.: жидкости, стёкла, аморфные тела, жидкие кристаллы и кристаллы. Основное различие между аморфными телами и кристаллами, заключается в отсутствии дальнего порядка в аморфных телах и наличие его в кристаллах. Введены понятия текучести, предела текучести, упругой и пластической деформации твердого тела, ближнего и дальнего порядка. С помощью теоретических выкладок доказывается, что конденсированная фаза является наиболее энергетически выгодным состоянием системы взаимодействующих частиц. Конденсированная фаза с упорядоченным расположением частиц в основном состоянии, (т.е. при температуре Т=0) чаще всего представляет собой кристаллическую фазу. Поскольку, связи атомов на внешней границе кристалла не заняты («оборваны»), следовательно, поверхностная энергия кристалла весьма существенна, поэтому энергетически более выгодно существование поликристаллов (агрегатов, состоящие из большого числа маленьких кристаллических зерен, ориентированных друг относительно друга хаотически), т.к. при этом “торчащие” энергии монокристаллов компенсируются. Большинство твердых технических материалов являются поликристаллическими.

Тест

Вопрос 1. Являются ли жидкости структурно упорядоченными системами.

Варианты ответов: да, нет

Вопрос 2: Какой порядок присутствует в аморфных телах:

Варианты ответов: Дальний, ближний, частично тот и другой

Вопрос 3: Какой порядок соблюдается в кристаллитах

Варианты ответов: дальний, ближний, оба

Вопрос 4: Образуется ли кристалл, если на графике зависимости энергии от межчастичного расстояния r нет минимума в области отрицательных энергий.

Варианты ответов: нет, да

Вопрос 5: является ли конденсированная фаза наиболее энергетически выгодным состоянием системы взаимодействующих частиц

Варианты ответов: да, нет

Лекция 2

Понятие решетки Бравэ. Основные типы кристаллических решеток.

Понятие элементарной ячейки является одним из основных понятий, связанных с кристаллами. Обобщенно элементарную ячейку можно описать, как минимальный объём кристалла, многократные трансляции (параллельные переносы) которого в трёх измерениях позволяют построить всю кристаллическую решётку идеального кристалла. Такая формулировка соответствует сформулированным Бравэ 3 правилам выбора элементарных ячеек, выполняемые в следующей последовательности.

1.      Симметрия элементарной ячейки должна соответствовать симметрии кристалла.

2.      Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.

3.      При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.

Базис элементарной ячейки – это совокупность координат всех узлов, которые принадлежат элементарной ячейке.

Введено понятие обратной решетки - удобной абстракции, позволяющей математически наиболее просто описать условия протекания того или иного процесса в твердом кристаллическом теле. Между векторами элементарных трансляций   и параметрами обратной решетки существует  однозначная связь. Модули векторов  называются периодами элементарной ячейки, а углы между векторами элементарных трансляций , ,    углами элементарной ячейки. Если в кристаллической решетке все углы прямые, то вектора элементарных трансляций обратной решетки параллельны векторам прямой решетки и обратны им по величине. Все металлы представляют собой кристаллические тела, для которых характерен тот или иной тип кристаллической решетки, состоящей из малоподвижных положительно заряженных ионов, между которыми движутся свободные электроны (электронный газ). Тип решетки определяется формой элементарной ячейки (элементарного геометрического тела), многократное повторение (трансляции) которой по трем пространственным осям образует решетку данного кристаллического тела. Различают несколько типов кристаллических решеток: кубическая (приходится 1 атом на ячейку), объемно-центрированная кубическая (ОЦК, 2 атома на ячейку), гранецентрированная кубическая (ГЦК, 4 атома на ячейку), гексагональная плотноупакованная (ГП, 6 атомов на ячейку). Введены понятия компактность кристаллической решетки или степень заполненности ее объема атомами, параметр ячейки, координационное число.

Тест

Вопрос 1. Может ли примитивная ячейка иметь дополнительные узлы внутри себя или на поверхности

Варианты ответов: да, нет

Вопрос 2. Может ли элементарная ячейка иметь дополнительные узлы внутри себя или на поверхности

Варианты ответов: да, нет

Вопрос 3: Может ли элементарная ячейка содержать боле 1 атома

Варианты ответов: да, нет

Вопрос: Является ли решетка, обратная обратной решетке, исходной (прямой) решеткой.

Варианты ответов: да, нет

Вопрос: Сколько атомов на ячейку приходится в ГЦК решетке

Варианты ответов: 1, 2, 3, 4, 8

Вопрос: чему равно координационное число ОЦК решетки

Варианты ответов: 4, 8, 12

Лекция 3

Свойства колебаний решетки на примере моноатомного линейного кристалла

Аннотация.

Атомы в твердом теле при любой температуре непрерывно совершают колебания около среднего положения равновесия- узлов кристаллической решетки. Для того чтобы понять свойства колебаний решетки вначале полезно изучить несколько простых случаев, одним из которых является одноатомный линейный кристалл. На этом простом примере введены понятия зоны Бриллюэна, фазовой и групповой скоростей. С помощью рассмотрения колебания одномерной моноатомной цепочки определено, что зависимость частоты  колебаний от волнового числа k для дискретной цепочки атомов является нелинейной и периодической, показано существование разрешенных частот, а следовательно, существование разрешенных энергий (поскольку частоты и энергии волн пропорциональны). Границе зоны Бриллюэна соответствуют предельные значения частоты. Значения длин волн, распространяющихся вдоль одномерной цепочки одинаковых атомов, лежат в пределах от удвоенного периода цепочки до длины цепочки.

Тест

Вопрос 1. Частота колебаний в одномерной моноатомной цепочке равна

Варианты ответов: , ,

Вопрос 2: Чему равна минимальная длина волны, распространяющейся вдоль одномерной цепочки одинаковых атомов

Варианты ответов: a, 2a, 4a

Вопрос 3: чему равна максимальная длина волны, распространяющаяся в одномерной моноатомной цепочке из N атомов длиной L

Варианты ответов: L/4, L/2, L, 2L

Вопрос 4

Фазовая скорость для колебаний, распространяющаяся в одномерной моноатомной цепочке равна

Варианты ответов , ,

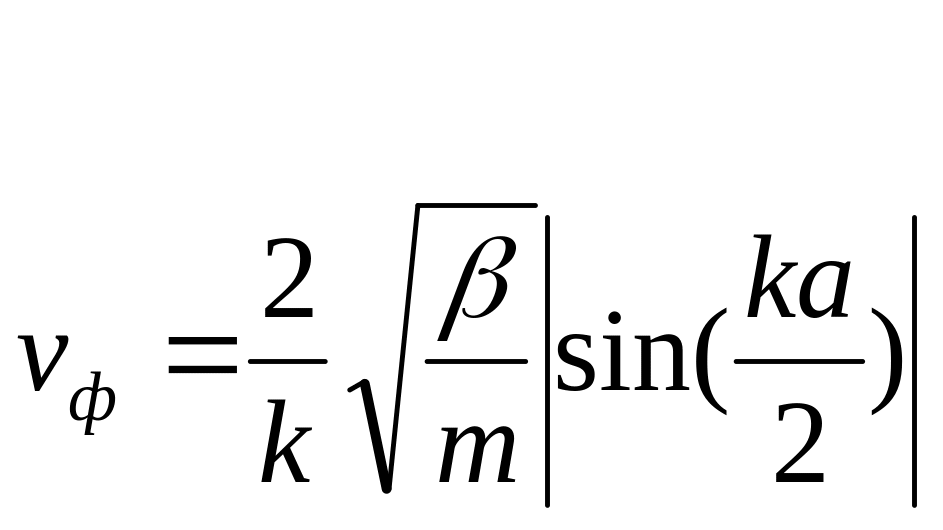Вопрос 5 групповая скорость распространения волны в одномерной моноатомной цепочке равна

Варианты ответов: , ,

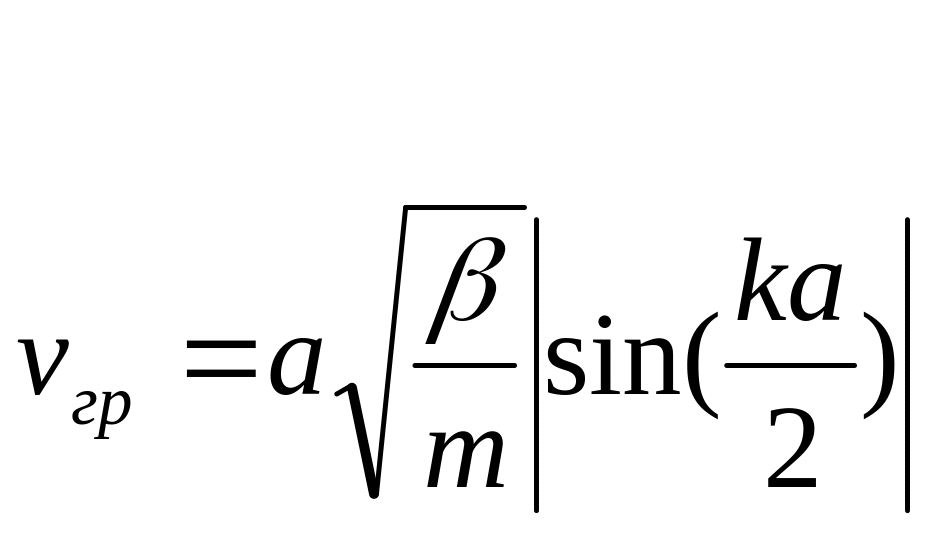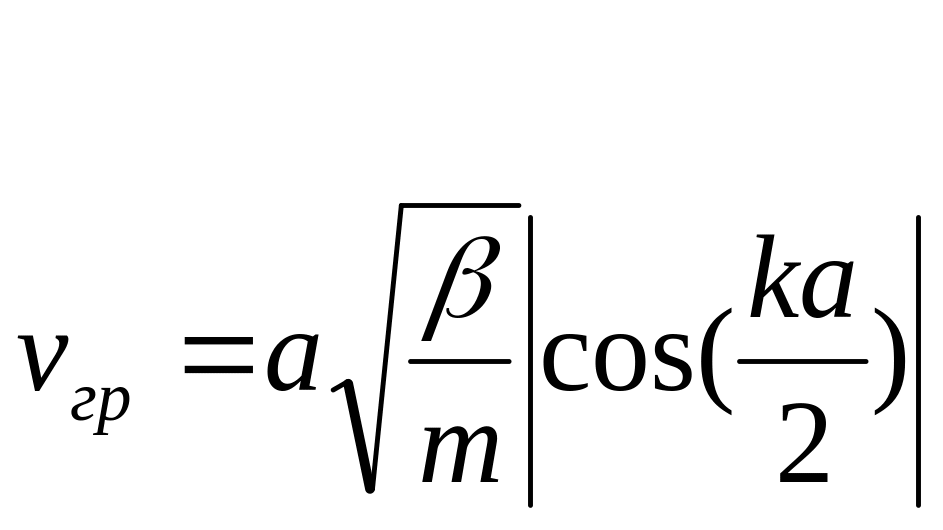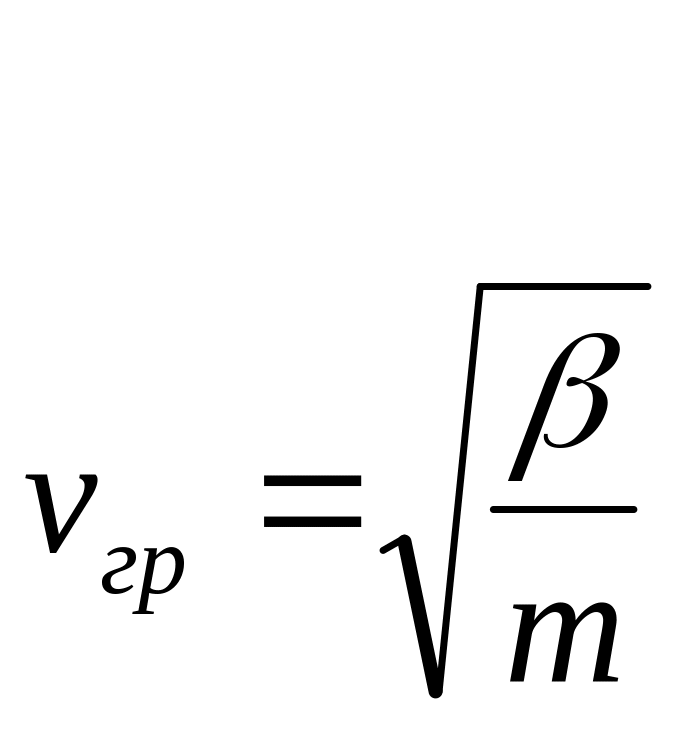
Задание на семинар

Определение фазовой и групповой скоростей в предельных случаях малых значений волнового числа (k 0) и на границе зоны Бриллюэна при значении волнового числа , а также при k=/(4a), а –период цепочки.

Лекция 4

Свойство колебаний решетки на примере двухатомного линейного кристалла, колебательный спектр, акустическая и оптическая ветви колебаний

Рассматривается линейная двухатомная цепочка (которая моделирует двухатомный кристалл), состоящая из двух типов частиц с различными массами. В приближении взаимодействия с ближайшими соседями, малости смещения атомов из их положения равновесия и квазиупругости сил взаимодействия получаем значения частот распространяющихся волн:

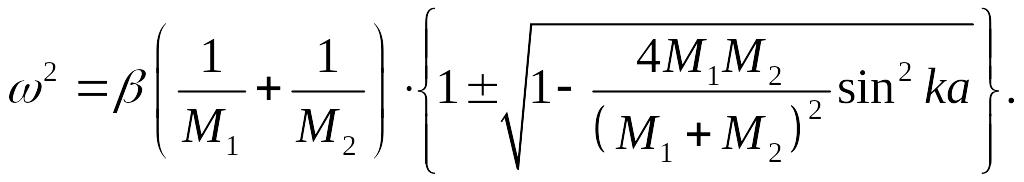
Для того, чтобы пояснить название ветвей и , рассматривается предельный случай малости волнового числа k0 и рассчитываются отношения амплитуд смещений атомов разного сорта для ветвей и . При этом выяснено, что в случае колебания с колебания соседних атомов происходят в фазе и имеют приблизительно одинаковые амплитуды. Это характерно для акустической волны, что и было причиной названия ветви колебаний акустической ветвью. В то время как при колебаниях с соседние атомы (атомы разного сорта) колеблются в противофазе и центр масс системы из 2-х атомов разных сортов остается неподвижным. Такие колебания характерны при возбуждении в ионных кристаллах электрическим полем световой волны. Поэтому ветвь колебаний получила название оптической. Определен набор длин волн, которые могут распространяться в цепочке из атомов двух сортов и показано, что минимальная длина волны, распространяющейся в такой цепочке вдвое больше, чем в моноатомной цепочке. Рассмотрены групповая и фазовая скорости распространения колебаний в линейной двухатомной цепочке и построены дисперсионные кривые (k) для двухатомной одномерной цепочки

Тест

Вопрос 1. Формула для зависимости значения частот распространяющихся волн в линейной двухатомной цепочке, состоящей из двух типов частиц с различными массами M₁< M₂, от значения волнового вектора

Варианты ответов:

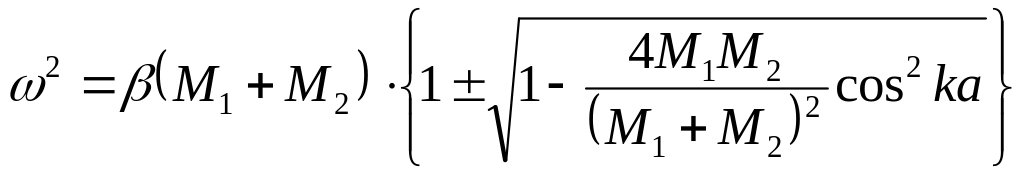
_{Вопрос 2. Какая из ветвей колебаний называется оптической}

Варианты ответов ,

Вопрос 3. полоса запрещенных частот распространяющихся волн в линейной двухатомной цепочке, состоящей из двух типов частиц с различными массами M₁< M₂ лежит в пределах

Варианты ответов

от до

от до

от 0 до

Вопрос 4. Чему равна минимальная длина волны, распространяющейся вдоль двухатомной цепочке, состоящей из двух типов частиц с различными массами

Варианты ответов: a, 2a, 4a

Вопрос 5: чему равна максимальная длина волны, распространяющаяся в двухатомной цепочке длиной L

Варианты ответов: L/4, L/2, L, 2L

Вопрос 6. групповая скорость распространения оптической волны в двухатомной цепочке, состоящей из двух типов частиц с различными массами в центре (при ) и у границ ( ) зоны Бриллюэна равна

Варианты ответов: +скорость звука, 0, - скорость звука

Вопрос 7. Чему равна фазовая скорость оптической ветки колебаний в двухатомной цепочке, состоящей из двух типов частиц с различными массами в центре (при ) зоны Бриллюэна

Варианты ответов: 0, , скорость звука

Лекция 5 Колебания системы дискретных частиц. Приближение Борна — Оппенгеймера (вариация адиабатического приближения) и гармоническое приближение.

Любое твердое тело можно представить как систему колеблющихся дискретных частиц, поскольку неподвижность атомов, составляющих твердое тело противоречит основным постулатам квантовой теории. Поэтому полезно иметь представление о некоторых часто применяемых приближениях. В данной лекции рассмотрены адиабатическое и гармоническое приближения. Обычно в физике суть адиабатического приближения заключается в постоянстве какой-либо величины. В физике конденсированного состояния адиабатическое приближение представляет собой приближение Борна — Оппенгеймера ( вариация адиабатического приближения уравнения Шрёдингера в квантовой механике), который заключается в выделении и отдельном описании ядер атомов и электронов, поскольку для них характерные времена изменения состояния сильно различаются. Вследствие того, что масса ядра существенно превышает массу электрона, электроны движутся гораздо быстрее и успевают почти мгновенно подстроиться под любое изменение координат ядер. Поэтому в данном приближении медленно колеблющиеся (и вращающиеся) ядра образуют электростатическое поле в котором движутся электроны. С точки зрения квантовой механики адиабатическое приближение означает, что полная волновая функция молекулы может быть выражена в виде произведения электронной и ядерной функций. По-иному говоря, вклад электронов в перенос массы пренебрежимо мал, однако, перенос заряда обусловлен чисто электронным вкладом. Исходя из вероятности «размытости» фермиевской ступеньки (на графике «число частиц – энергия») оценено количество электронов в металле, которые не отслеживают движение ионов в узлах кристаллической решетки и получено значение 0.1% общего количества электронов. Таким образом, доказывается, что адиабатическое приближение (приближение Борна — Оппенгеймера) в металлах применимо. С помощью рассмотрения силы, действующей на ион в узле кристаллической решетки (или атом в положении равновесия) и записи разложения потенциальной энергии вблизи точки равновесия r=r₀ для малых отклонений от точки равновесия вводится понятие гармонического приближения.

,  , 

Тогда сила, действующая на атом при его колебании вблизи положения равновесия запишется в виде:

В данном случае рассмотрения колебаний атомов вблизи их положений равновесия гармоническое приближение заключается в учете только линейного члена, т.е. , при этом силу F называют квазиупругой.

Итак, суммируя вышесказанное:

гармоническими колебаниями называются колебания под действием возвращающей силы, пропорциональной смещению.

основные положения гармонического приближения колебаний атомов заключаются в следующем:

средние равновесные расстояния между соседними атомами отвечают минимуму кривой потенциальной энергии U(r) и соответствуют статистической модели кристалла;

атомы колеблются относительно положений своих центров тяжести (усредненные значения для каждого атома), при малости амплитуды колебаний можно ограничиться учетом только квадратичного члена в разложении потенциальной энергии U(r) по степеням отклонений атома от положения равновесия , при этом в силе учитывается только линейный член и сила называется квазиупругой.

Гармоническое приближение дает хорошие результаты при сравнении с экспериментальными данными во многих случаях. Однако тепловое расширение кристаллов требует учета кубического слагаемого в выражении для потенциальной энергии U(r) - такое приближение называют ангармоническим.

Тест