2.6. Интегрирование иррациональных выражений

Основным методом интегрирования иррациональных выражений является сведение их к интегралу от функции, не содержащей иррациональностей, путем введения некоторой замены.

Рассмотрим следующие способы интегрирования иррациональных выражений.

Подынтегральная функция содержит . В этом случае замена позволит избавиться от корня.

Пример.

Вычислить интеграл .

Решение.

Введем замену: тогда

После замены переменной получаем интеграл:

.

Пример.

Вычислить интеграл .

Решение.

Здесь замена позволит избавиться от корней:

.

Разделив в столбик числитель на знаменатель, получим

Интегралы, содержащие квадратный трехчлен, вычисляются выделением полного квадрата в подкоренном выражении.

Пример.

Вычислить интеграл .

Решение.

Интегралы, содержащие вычисляются путем замены или Интегралы, содержащие вычисляются путем замены

Пример.

Вычислить интеграл .

Решение.

Выделяя полный квадрат в подкоренном выражении, получим

.

Далее сделаем замену , тогда

Задачи.

Применяя различные подстановки, вычислить следующие интегралы:

8.127. ; 8.128. ;

8.129. ; 8.130. ;

8.131. ; 8.132. ;

8.133. ; 8.134. ;

8.135. ; 8.136. ;

8.137. ; 8.138. ;

8.139. ; 8.140. ;

8.141. ; 8.142. ;

8.143. ; 8.144. .

2.7. Интегрирование тригонометрических выражений

Интегралы вида где хотя бы одно из чисел m или n – нечетно, вычисляются так: отделяя от нечетной степени один сомножитель заносим его под знак дифференциала, и, выражая с помощью формулы оставшуюся четную степень, приходим к табличному интегралу.

Например,

.

Пример.

Вычислить интеграл .

Решение.

Замена приводит интеграл к виду:

Интегралы вида где m и n – четные числа, вычисляются с помощью формул понижения степени:

Пример.

Вычислить интеграл .

Решение.

Интегралы вида

вычисляются путем преобразования произведения тригонометрических функций в сумму:

.

.

.

Пример.

Вычислить интеграл .

Решение.

.

Универсальная тригонометрическая подстановка.

Подстановка позволяет свести интегралы от тригонометрических выражений к интегралам от функции, не содержащей тригонометрических выражений. При этом используются формулы:

; .

Замечание: если интеграл содержит тригонометрические функции только в четных степенях, то удобнее использовать подстановку . В этом случае

; ; .

Пример.

Вычислить интеграл .

Решение.

Используя универсальную подстановку, получим:

.

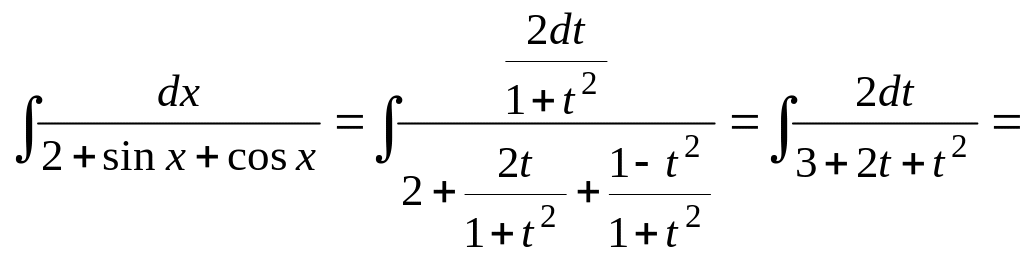
Задачи.

Вычислить интегралы от тригонометрических выражений:

8.145. ; 8.146. ;

8.147. ; 8.148. ;

8.149. ; 8.150. ;

8.151. ; 8.152. ;

8.153. ; 8.154. ;

8.155. ; 8.156. ;

8.157. ; 8.158. ;

8.159. ; 8.160. .

Вычислить следующие интегралы, применяя различные методы:

8.161. ; 8.162. ;

8.163. ; 8.164. ;

8.165. ; 8.166. ;

8.167. ; 8.168. ;

8.169. ; 8.170. ;

8.171. ; 8.172. ;

8.173. ; 8.174. ;

8.175. ; 8.176. ;

8.177. ; 8.178. ;

8.179. ; 8.180. ;

8.181. ; 8.182. ;

8.183. ; 8.184. ;

8.185. ; 8.186. ;

8.187. ; 8.188. ;

8.189. ; 8.190. ;

8.191. ; 8.192. .

121