
- •Глава VIII Неопределенный интеграл
- •1. Первообразная. Неопределенный интеграл и его свойства
- •2. Методы вычисления неопределенных интегралов
- •2.1. Непосредственное интегрирование
- •2.2. Метод подведения под знак дифференциала
- •2.3. Метод замены переменной
- •2.4. Метод интегрирования по частям
- •2.5. Интегрирование рациональных дробей. Метод неопределенных коэффициентов
- •2.6. Интегрирование иррациональных выражений
- •2.7. Интегрирование тригонометрических выражений
Глава VIII Неопределенный интеграл
1. Первообразная. Неопределенный интеграл и его свойства
Функция
![]() называется первообразной функции
называется первообразной функции
![]() на интервале
на интервале
![]() если
дифференцируема на
если
дифференцируема на
![]() и справедливо равенство
и справедливо равенство
![]() .
.
Если
– какая–либо первообразная для
,
то любая другая первообразная для
имеет вид
![]() где
где
![]()
Произвольная первообразная для
на
![]() называется неопределенным интегралом
от функции
и обозначается символом
называется неопределенным интегралом
от функции
и обозначается символом
![]()
Здесь знак
![]() знак интеграла,
знак интеграла,
![]() – подынтегральное выражение;
– подынтегральная функция.
– подынтегральное выражение;
– подынтегральная функция.
Если – одна из первообразных для , то
![]()
где
![]() – произвольная константа.
– произвольная константа.
Операцию нахождения неопределенного интеграла от данной функции называют интегрированием этой функции. Интегрирование – операция, обратная операции дифференцирования. У всякой непрерывной на данном интервале функции существует неопределенный интеграл.
Свойства неопределенного интеграла
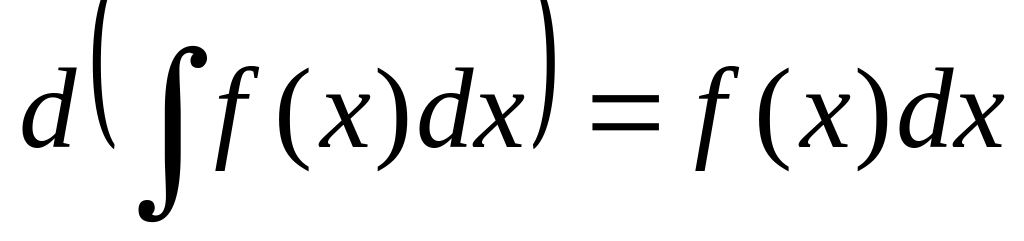 ;
;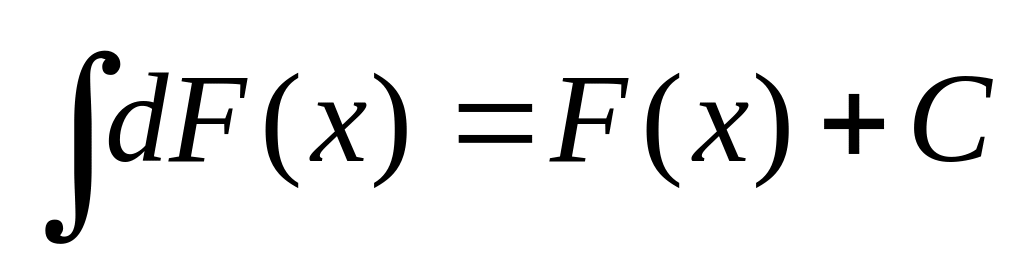 ;
;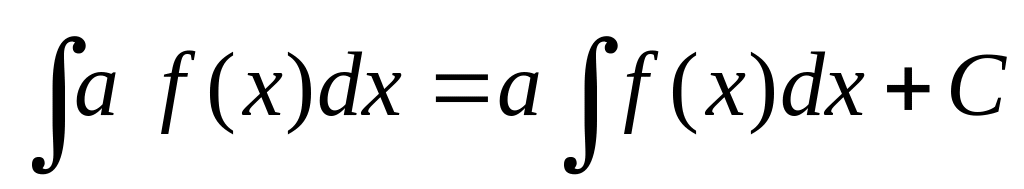 ;
;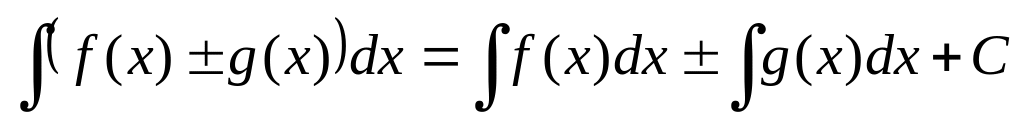 .
.
Свойства 3) и 4) называют свойствами линейности неопределенного интеграла.
Таблица основных неопределенных интегралов
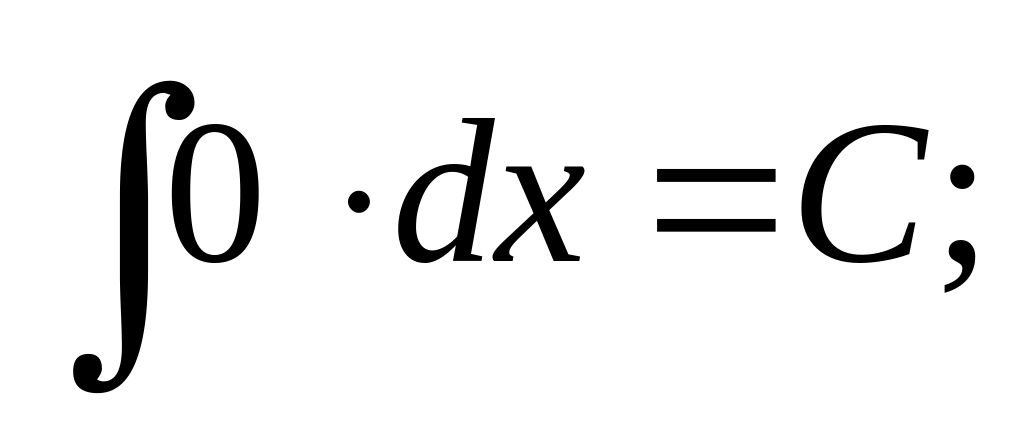
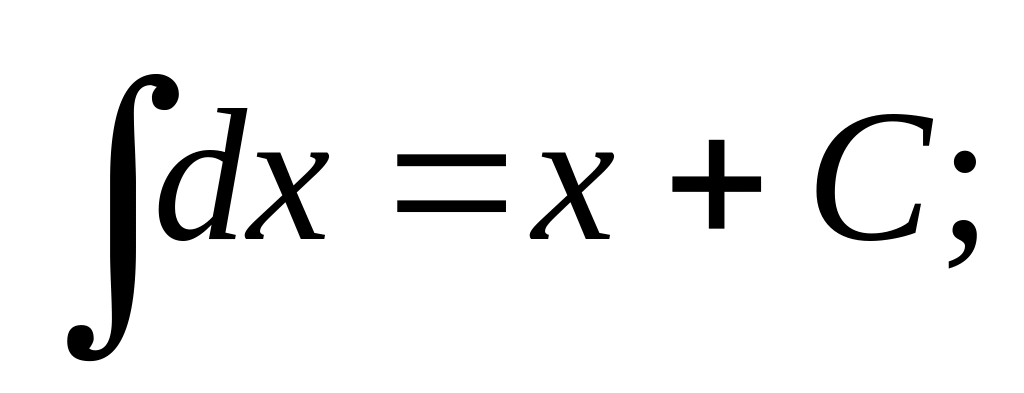
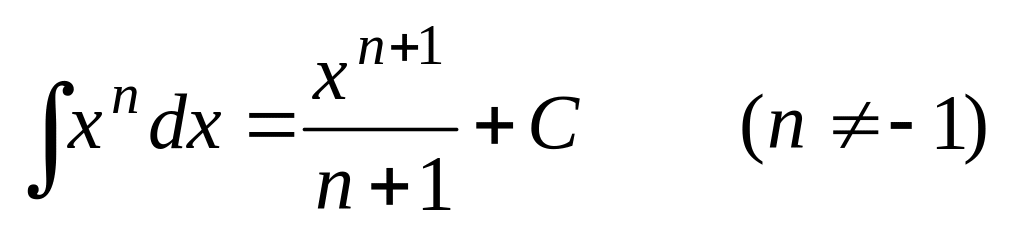 ,
,
в частности, ![]()
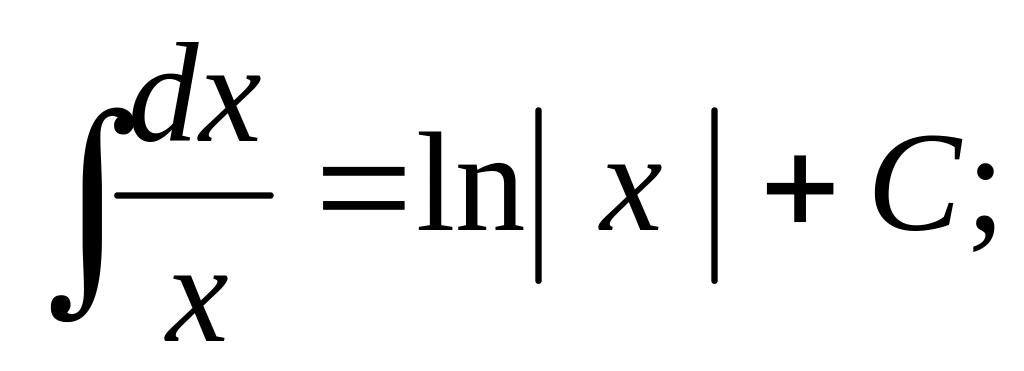
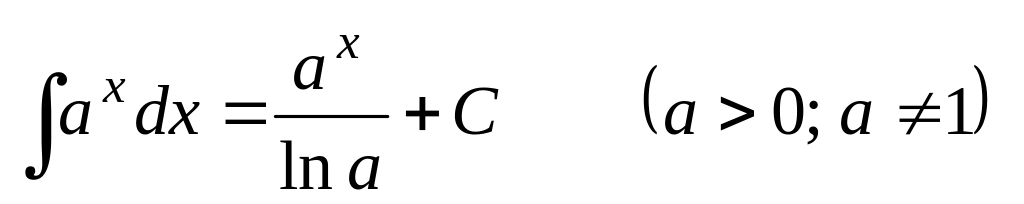 ,
,
в частности, ![]()
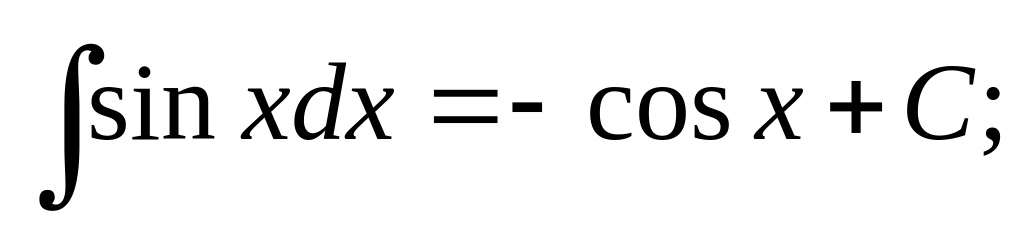
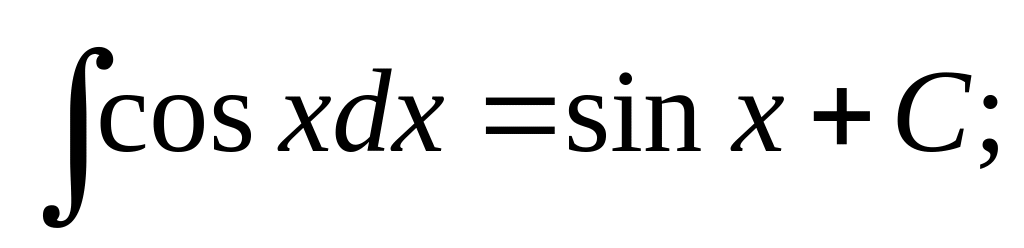
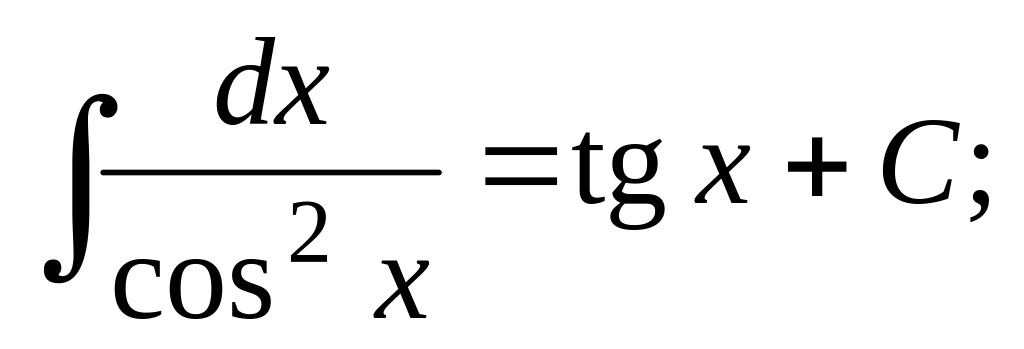
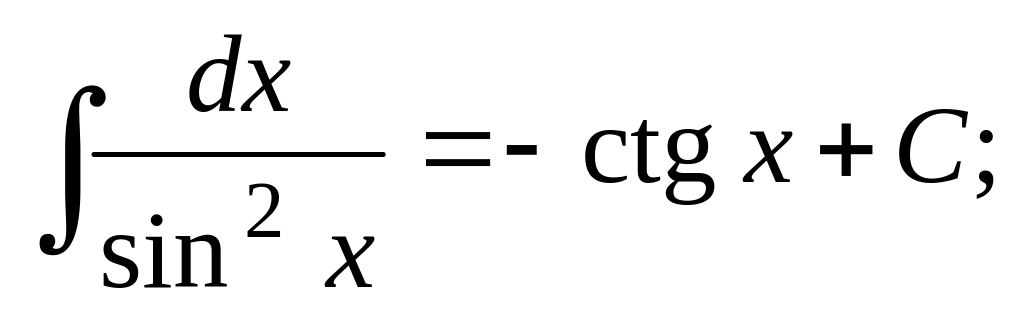
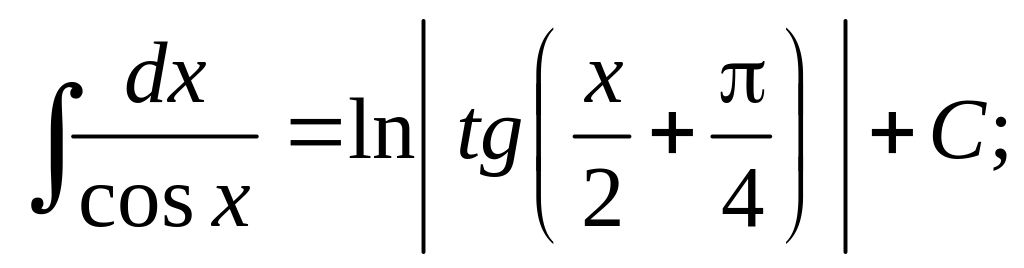
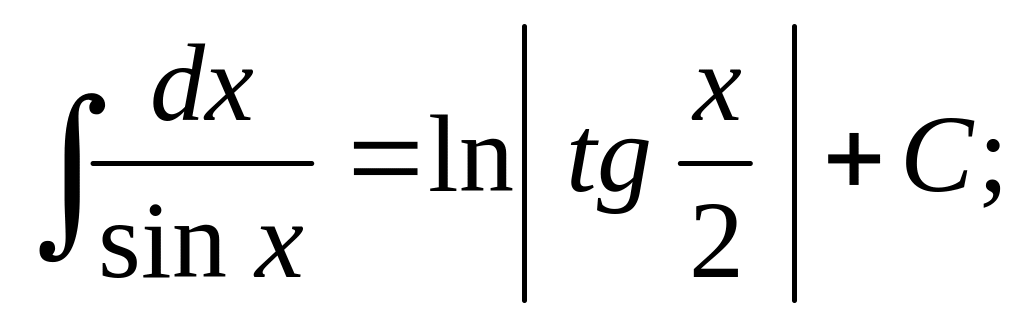
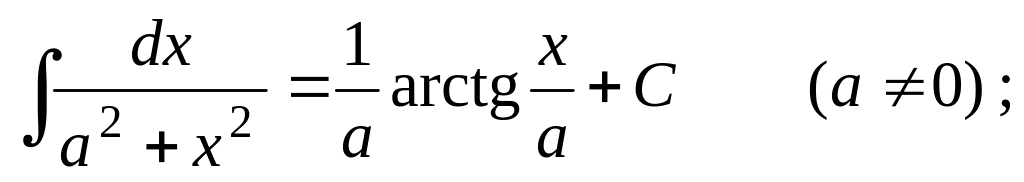
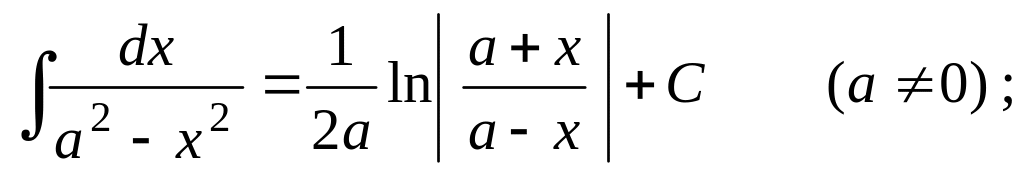
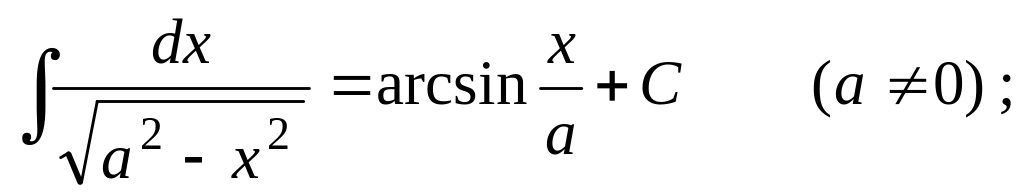
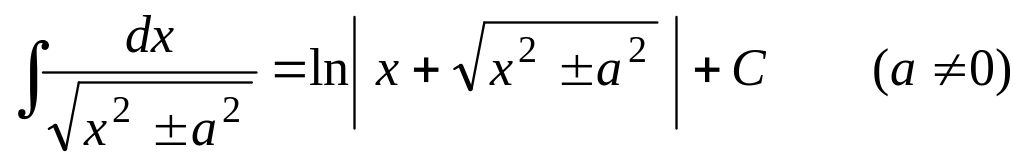 ;
;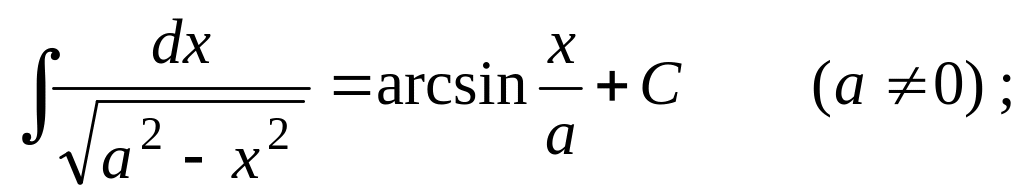
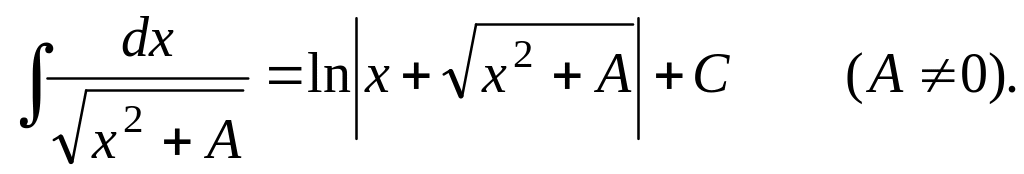
2. Методы вычисления неопределенных интегралов
2.1. Непосредственное интегрирование
Вычисление неопределенных интегралов с использованием таблицы интегралов и свойств, приведенных выше, называют непосредственным интегрированием. Рассмотрим некоторые примеры.
Пример.
Вычислить
интеграл:
![]()
Решение.
Преобразуем
подынтегральную функцию
![]() .
Тогда
.
Тогда
![]() .
.
Далее воспользуемся свойствами линейности и формулой 3 таблицы интегралов.
![]() .
.
Пример.
Вычислить интеграл:
![]() .
.
Решение.
Прежде всего, разделим почленно числитель на знаменатель в подынтегральной функции:
![]()
Преобразуем каждое слагаемое и воспользуемся свойством линейности:
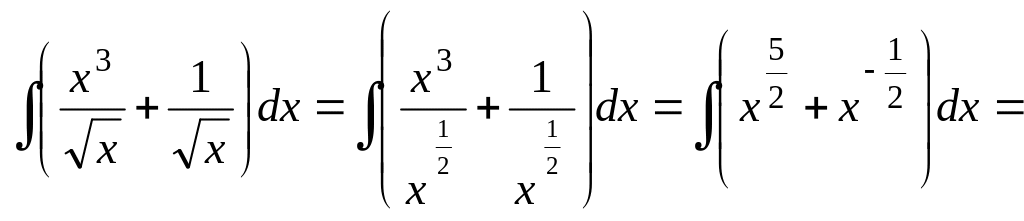
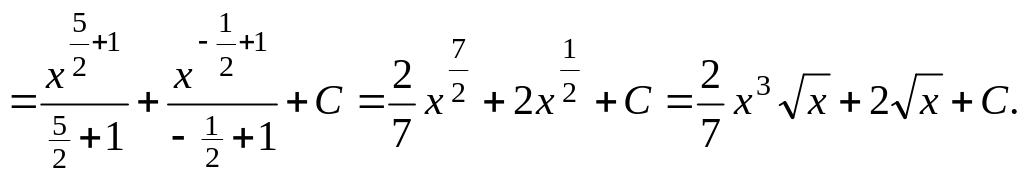
Задачи.
Вычислить неопределенные интегралы:
8.1.
![]() ; 8.2.
; 8.2.
![]() ;
;
8.3.
![]() ; 8.4.
; 8.4.
![]() ;
;
8.5.
![]() ; 8.6.
; 8.6.
![]() ;
;
8.7.
![]() ; 8.8.
; 8.8.
![]() ;
;
8.9.
![]() ; 8.10.
; 8.10.
![]() ;
;
8.11.
![]() ; 8.12.
; 8.12.
![]() ;
;
8.13.
![]() ; 8.14.
; 8.14.
![]() ;
;
8.15.
![]() ; 8.16.
; 8.16.
![]() .
.
2.2. Метод подведения под знак дифференциала
Напомним,
что для дифференциала
![]() функции
справедлива формула:
функции
справедлива формула:
![]()
Часто при нахождении неопределенного интеграла возможно преобразование интеграла к виду
![]()
Преобразование проводится таким образом,
чтобы в интеграле
![]() рассматривался новый аргумент
рассматривался новый аргумент
![]() ,
который вычисляется с помощью таблицы
интегралов.
,
который вычисляется с помощью таблицы
интегралов.
Чтобы операция подведение под знак дифференциала не вызывала трудностей, необходимо выучить таблицу производных. Из нее, очевидно, следуют формулы для наиболее часто встречающихся дифференциалов:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Следует помнить, что если к функции, стоящей под знаком дифференциала, прибавить любую константу, то дифференциал не изменится:
![]()
Пример.
Вычислить
интеграл:
![]() .
.
Решение.
Этот интеграл вычислим методом подведения под знак дифференциала, умножим и разделим его на 7.
![]() .
.
Теперь, если
![]() считать новым аргументом, интеграл
можно вычислить по формуле 7 таблицы
интегралов.
считать новым аргументом, интеграл
можно вычислить по формуле 7 таблицы
интегралов.
![]()
Следует помнить, что если к функции, стоящей под знаком дифференциала, прибавить константу, то дифференциал от этого не изменится.
Задачи.
Внести следующие функции под знак дифференциала:
8.17.
![]() ; 8.18.
; 8.18.
![]() ;
;
8.19.
![]() ; 8.20.
; 8.20.
![]() ;
;
8.21.
![]() ; 8.22.
; 8.22.
![]() ;
;
8.23.
![]() ; 8.24.
; 8.24.
![]() ;
;
8.25.
![]() ; 8.26.
; 8.26.
![]() .
.
Пример.
Вычислить
интеграл:
![]() .
.
Решение.
Поскольку в
знаменателе присутствует
![]() желательно под знаком дифференциала
также получить
поэтому
желательно под знаком дифференциала
также получить
поэтому
![]() .
Далее прибавим под знаком дифференциала
5, т.е.
.
Далее прибавим под знаком дифференциала
5, т.е.
![]() .
Тогда
.
Тогда
![]()
Пример.
Вычислить интеграл:
![]()
Решение.
![]()
Задачи.
Вычислить неопределенные интегралы:
8.27.
![]() ; 8.28.
; 8.28.
![]() ;
;
8.29.
![]() ; 8.30.
; 8.30.
![]() ;
;
8.31.
![]() ; 8.32.
; 8.32.
![]() ;
;
8.33.
![]() ; 8.34.
; 8.34.
![]() ;
;
8.35.
![]() ; 8.36.
; 8.36.
![]() ;
;
8.37.
![]() ; 8.38.
; 8.38.
![]() ;
;
8.39.
![]() ;
8.40.
;
8.40.
![]() ;
;
8.41.
![]() ; 8.42.
; 8.42.
![]() ;
;
8.43.
![]() ; 8.44.
; 8.44.
![]()
