Глава VII
Производная функции
1. Определение производной
Пусть
дана функция
,
определенная в точке
и ее окрестности. Изменим значение
аргумента с
до
.
Величина, показывающая, насколько
изменился аргумент, называется приращением
аргумента и
обозначается
.
Таким образом,
.
При данном изменении аргумента значение
функции изменится на величину
,
называемую приращением
функции. Величины
и
не обязательно положительные.
Производной функции в точке называется предел отношения приращения этой функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Пример.
Пользуясь
определением, найти производную функции
.
Решение.
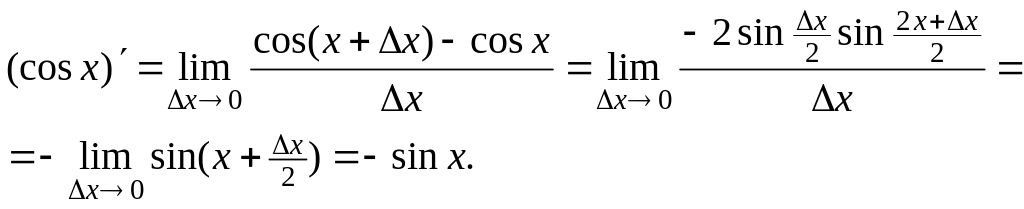
Числа
и
называются соответственно левой
и
правой производными функции
в
точке
.
Для существования производной функции
в точке
необходимо
и достаточно, чтобы ее левая и правая
производные в этой точке существовали
и совпадали, т.е.
.
Функция, имеющая производную в точке , называется дифференцируемой в этой точке. Процесс нахождения производной называют дифференцированием.
Связь между дифференцируемостью и непрерывностью
Теорема. Если функция дифференцируема в некоторой точке, то она и непрерывна в этой точке.
Обратное утверждение неверно.
Пример.
Покажем,
что непрерывная функция
(рис.15) не является дифференцируемой в
точке
.
Решение.
.
Найдем правую и левую производные:
.
Эти производные существуют, но не совпадают. Значит, в точке данная функция не имеет производной.
Функция является непрерывной, т.к.
.
2. Таблица производных
1.
в
частности,
.
2.
в
частности,
.
3.
в
частности,
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
3. Правила дифференцирования функций
I.
Пусть С
– постоянная и
– дифференцируемые функции. Тогда:
1.
2.
.
3.
.
4.
.
5.
.
II. Правило дифференцирования сложной функции:
Пусть
функция
имеет производную в точке
,
а функция
имеет производную в точке
.
Тогда сложная функция
в точке
имеет производную, равную
.
Пример.
Найти производные следующих функций:
а)
; б)
; в)
.
Решение.
а) Используя правило дифференцирования 4, получим
.
б) По правилу дифференцирования 5 имеем
.
в) По правилу дифференцирования сложной функции, полагая
,
получим
.
4. Геометрический смысл производной
Касательной
к графику функции
в точке
называется предельное положение секущей
ММ0,
когда
по кривой
.
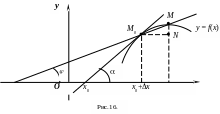
Пусть
(рис.16). Из
имеем
.
Если
,
то
,
где
– угол
наклона касательной к графику функции
в точке
к оси Ох,
т.е.
.
Значение
производной
равно угловому коэффициенту касательной
к графику данной функции в точке
.
Уравнение касательной к кривой в точке имеет вид:
.
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Уравнение нормали имеет вид:
,
при условии
.
x
Пусть
даны две пересекающиеся в точке
кривые
и
,
причем обе функции имеют производные
в этой точке. Тогда углом между этими
кривыми называется угол между касательными
к ним, проведенными в точке
:
.
Пример.
Написать
уравнения касательной и нормали к кривой
в
точке
.
Решение.
Так
как
,
то
,
а
.
Получаем уравнение касательной:
или
и уравнение нормали:
или
.
Пример.
Найти
угол, под которым пересекаются кривая
и прямая
.
Решение.
Найдем
точку пересечения графиков этих функций.
Для этого решим уравнение
.
Теперь найдем уравнение касательной к
графику функций
в точке
.
Т.к.
,
то
;
.
Значит, уравнение касательной имеет
вид
.
Угол,
под которым пересекаются в точке
прямая
и касательная
и является искомым углом. Так как
и
,
то
.
Задачи.
Пользуясь
только определением производной, найти
:
7.1.
; 7.2.
;
7.3.
; 7.4.
;
7.5.
; 7.6.
;
7.7.
; 7.8.
.
Найти производные следующих функций:
7.9.
; 7.10.
;
7.11.
; 7.12.
;
7.13.
; 7.14.
;
7.15.
; 7.16.
;
7.17.
; 7.18.
;
7.19.
; 7.20.
;
7.21.
; 7.22.
;
7.23.
; 7.24.
;
7.25.
; 7.26.
;
7.27.
; 7.28.
;
7.29.
; 7.30.
;
7.31.
; 7.32.
;
7.33.
; 7.34.
;
7.35.
; 7.36.
;
7.37.
; 7.38.
;
7.39.
; 7.40.
.
7.41. Найти производные гиперболических функций:
а)
; б)
;
в)
; г)
.
Написать уравнения касательной и нормали к графику функции в данной точке и сделать рисунок:
7.42.
; 7.43.
;
7.44.
; 7.45.
;
7.46.
; 7.47.
.
Найти углы, под которыми пересекаются заданные кривые:
7.48.
;
7.49.
;
7.50.
;
7.51.
.
5. Дифференциал функции
Пусть
функция
дифференцируема на интервале
.
Производная этой функции в некоторой
точке
определяется равенством
,
поэтому можно записать
,
где
при
.
Умножая все члены последнего равенства
на
,
получаем
.
Приращение состоит из двух слагаемых,
первое из которых при
есть главная часть приращения, линейная
относительно
.
Произведение
называется дифференциалом
функции и обозначается через
:
.
Т.к.
,
т.е. дифференциал независимой переменной
равен приращению этой переменной, то
.
Основное
использование дифференциала функции
– приближенные вычисления, т.к. при
справедливо приближенное равенство:
или
.
Пример.
Вычислить
приближенно:
.
Решение.
Пусть
,
.
Тогда
,
,
.
Используя свойство первого дифференциала, получаем
.
Задачи.
7.52.
Найти приращение
и дифференциал
в общем виде, а также в точке
,
если известно
:
а)
;
б)
;
в)
;
г)
.
Вычислить приближенно с помощью свойства дифференциала:
7.53.
; 7.54.
;
7.55.
; 7.56.
;
7.57.
; 7.58.
;
7.59.
; 7.60.
.