6. Прямая на плоскости
Прямая на плоскости в декартовой прямоугольной системе координат Оху (рис.5) может быть задана уравнением одного из следующих видов:
–
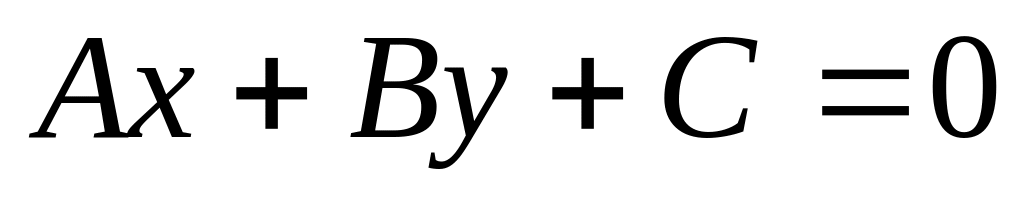общее
уравнение прямой;
–
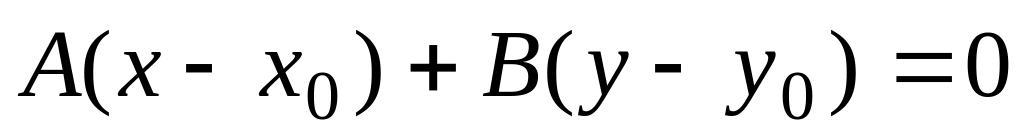уравнение
прямой, проходящей через точку
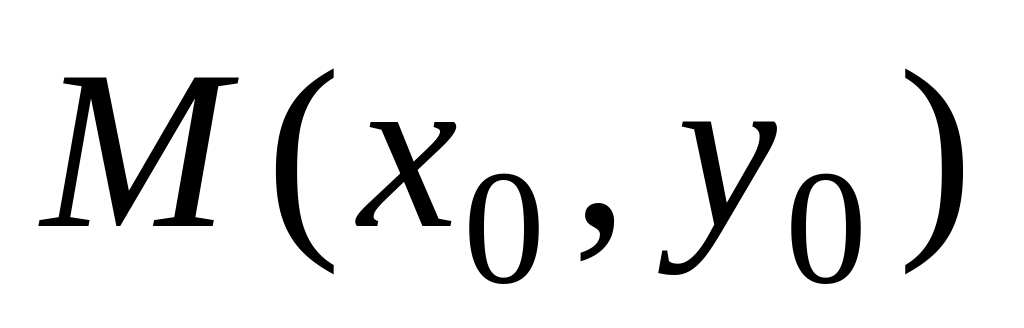перпендикулярно
нормальному
вектору
;
3)
–
уравнение
прямой, проходящей через точку
параллельно
направляющему
вектору
(каноническое
уравнение прямой);
4)
–
параметрические
уравнения
получили,
приравняв каждое из соотношений 3)
параметру t.
5)
–
уравнение
прямой в
отрезках,
где a
и
b
– длины отрезков, отсекаемых прямой на
координатных осях Ox
и
Oy
соответственно.
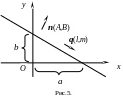
Расстояние d от точки до прямой вычисляют по формуле:
Задачи.
Написать уравнение прямой и привести его к общему виду:
2.43.
Прямая
L
задана
точкой
и
нормальным вектором
:
а) 
,
;
б) 
,
.
2.44. Прямая L задана точкой и направляющим вектором :
а) 
,
;
б) 
,
.
2.45.
Прямая
L
задана
двумя точками
и
:
а) 
,
;
б) 
,
.
Заданы прямая L и точка М. Требуется:
1) вычислить расстояние d(М, L) от точки М до прямой L;
2) написать уравнение прямой L', проходящей через точку М перпендикулярно заданной прямой L;
написать уравнение прямой L", проходящей через точку М параллельно заданной прямой L.
2.46. Исходные данные:
а) 
;
б) 
.
2.47. Исследовать взаимное расположение прямых L1 и L2. Если прямые параллельны, то найти расстояние между ними. Если прямые пересекаются, то найти точку пересечения и косинус угла между ними:
а)
;
б)
L1:
,
L2:
;
в)
;
г)
.
2.48. Дан треугольник с вершинами А(-2, 0), В(2, 4) и С(4, 0). Написать уравнения сторон треугольника, медианы АЕ, высоты AD и найти длину медианы АЕ.
2.49.
Найти углы и площадь треугольника,
стороны которого заданы уравнениями
.
2.50.
Показать, что точка
принадлежит прямой L:
.
Найти
соответствующее этой точке значение
параметра t.
2.51.
Вычислить расстояние от точки М(1,1)
до прямой L:
.
2.52.
Найти площадь треугольника, образованного
прямой
с осями координат.
2.53.
Написать уравнение прямой, отсекающей
на оси ординат отрезок
и образующей с положительным направлением
оси абсцисс угол 1200.
2.54.
Написать уравнение прямой, отсекающей
на осях координат равные отрезки, если
длина отрезка прямой, заключенного
между осями координат, равна
.
2.55. Написать уравнение прямой, проходящей через точку А(2, 4) и удаленной от начала координат на расстояние d = 2.
7. Плоскость и прямая в пространстве
Плоскость Р в декартовой прямоугольной системе координат Oxyz может быть задана уравнением одного из следующих видов:
– общее
уравнение плоскости;
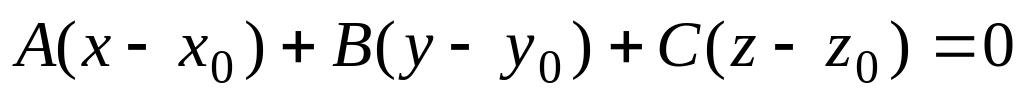– уравнение
плоскости, проходящей через точку
перпендикулярно
нормальному
вектоpy
;
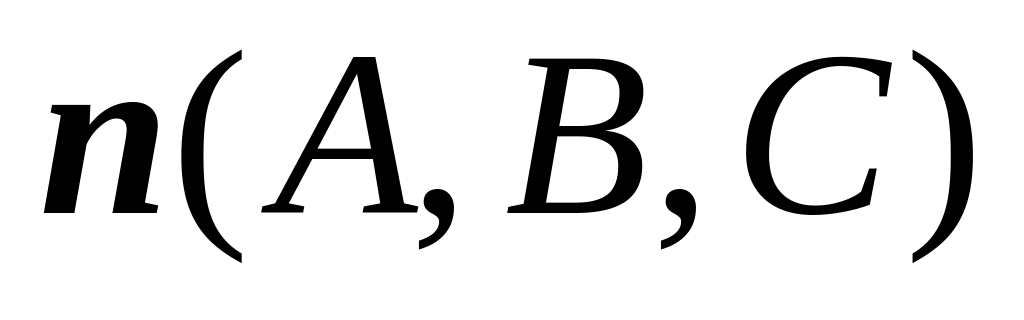– уравнение
плоскости в
отрезках,
где a,
b,
c
– величины
направленных отрезков, отсекаемых
плоскостью на координатных осях Ox,
Oy,
Oz
соответственно.
Расстояние
d(М,
Р)
от
точки
до
плоскости
вычисляют
по формуле:
Прямая L в пространстве может быть задана:
общими уравнениями
где
коэффициенты A1,
В1,
С1
не пропорциональны коэффициентам
,
что равносильно ее заданию как линии
пересечения плоскостей;
параметрическими уравнениями
где
–
направляющий вектор прямой;
каноническими уравнениями
Задачи.
2.56. Написать уравнение плоскости Р, проходящей через точку М параллельно заданной плоскости Р, и вычислить расстояние между Р и Р, если:
а) Р: –2x + y – z + 1 = 0, M(1, 1, 1);
б) Р: x – y – 1 = 0, M(1, 1, 2).
2.57. Написать уравнение плоскости Р, проходящей через заданные точки М1 и М2 перпендикулярно заданной плоскости Р, если:
а) Р: - x + y – 1 = 0, M1(1, 2, 0), M2(2, 1, 1);
б) Р: 2x – y + z + 1 = 0, M1(0, 1, 1), M2(2, 0, 1).
2.58. Написать уравнение плоскости, проходящей через точку М параллельно векторам а1 и а2, если:
а) M(1, 1, 1), а1(1, 2, 0), а2(2, 1, 1);
б) M(0, 1, 2), а1(0, 1, 1), а2(2, 0, 1).
2.59. Написать уравнение плоскости, проходящей через заданные точки М1 и М2 параллельно вектору а, если:
а) а(3, 0, 1), M1(1, 2, 0), M2(2, 1, 1);
б) а(0, –1, 2), M1(0, 1, 1), M2(2, 0, 1).
2.60. Написать уравнение плоскости, проходящей через три заданные точки М1, М2 и М3, если:
а) M1(1, 2, 0), M2(2, 1, 1), M3(3, 0, 1);
б) M1(1, 1, 1), M2(0, –1, 2), M3(2, 3, –1).
2.61. Исследовать взаимное расположение заданных плоскостей Р1 и Р2. Если плоскости параллельны, то найти расстояние между ними. Если плоскости пересекаются, то найти косинус угла между ними:
а)
Р1:
,
Р2:
;
б)
Р1:
,
Р2:
;
в)
Р1:
,
Р2:
.
2.62.
Найти расстояние от точки
до плоскости
.
2.63. Найти расстояние между параллельными плоскостями:
и 
.
2.64.
Написать уравнение плоскости, проходящей
через точку
и перпендикулярной к плоскостям
и
.
2.65. Написать канонические и параметрические уравнения прямой, проходящей через две заданные точки М1 и М2, если:
а) M1(1, –2, 1), M2(3, 1, –1); б) M1(3, –1, 0), M2(1, 0, –3).
2.66. Прямая задана общими уравнениями. Написать для этой прямой канонические уравнения, если:
а)
б)
2.67. Найти расстояние между параллельными прямыми:
и
2.68.
Доказать, что прямые параллельны и найти
расстояние между ними:
и
2.69.
Доказать, что прямые пересекаются и
найти точку их пересечения:
и
2.70. Найти угол между прямыми:
и 
2.71.
Написать уравнение прямой, проходящей
через точки пересечения плоскости
с прямыми:
и 
2.72.
Через прямую
провести плоскость, параллельную прямой
