Глава II Векторная алгебра и аналитическая геометрия

1. Векторы. Линейные операции над векторами

Вектором называется направленный отрезок. Вектор, имеющий началом точку A, а концом точку B обозначают или одной какой-нибудь буквой, например а, или . Модуль (длина) вектора обозначается , | а | или .

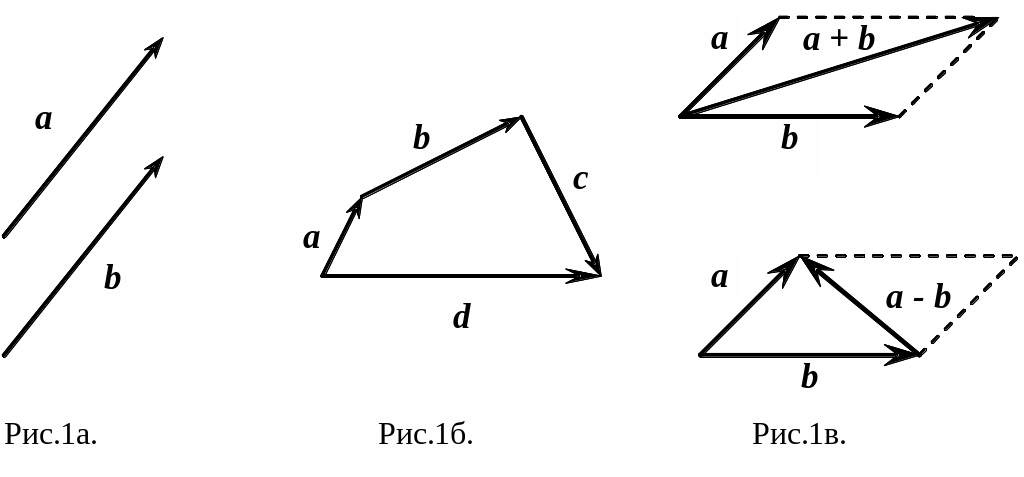
Векторы, параллельные одной прямой, называются коллинеарными. Векторы, параллельные одной плоскости, называются компланарными. Два вектора а и b (рис.1а) называются равными, если они имеют равные длины и сонаправлены.

Определим две основные операции векторной алгебры: умножение вектора на число и сложение векторов.

Произведением вектора а на число m называется новый вектор, имеющий длину и направленный одинаково с а (при ) или проти­воположно а (при ).

Суммой векторов называется вектор d (рис.1б), замыкающий ломаную, построенную из данных векторов. В частности, в параллелограмме, построенном на векторах a и b, одна вектор-диагональ есть сумма , а другая есть разность данных векторов (рис.1в).

2. Линейная зависимость векторов. Базис

Векторы называются линейно зависимыми, если существуют действительные числа ₁, ₂, …, _n, из которых, по меньшей мере, одно отлично от нуля, такие что

.

В противном случае (т. е. когда таких чисел не существует) векторы называются линейно независимыми; другими словами, векторы линейно независимы, если последнее равенство выполняется лишь в случае, когда

.

Сформулируем несколько основных свойств линейной зависимости векторов.

1. Векторы линейно зависимы тогда и только тогда, когда, по меньшей мере, один из них является линейной комбинацией остальных.

2. Два вектора a и b линейно зависимы тогда и только тогда, когда они коллинеарны.

3. Если и – два неколлинеарных вектора некоторой плоскости, то любой третий вектор этой же плоскости можно единственным образом разложить по ним, т.е. представить в виде

.

4. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

5. Если векторы некомпланарны, то любой вектор a в пространстве можно единственным образом разложить по ним, т.е.

.

6. Всякие четыре вектора в пространстве линейно зависимы.

В пространстве любая упорядоченная система трех линейно независимых (т.е. некомпланарных) векторов называется базисом. Согласно свойству 5, всякий вектор d можно разложить по базису, т.е. представить в виде

.

Числа называют координатами вектора d в базисе .

Базис ( ) называется прямоугольным, если векторы и попарно перпендикулярны и имеют единичную длину. В этом случае приняты обозначения:

.

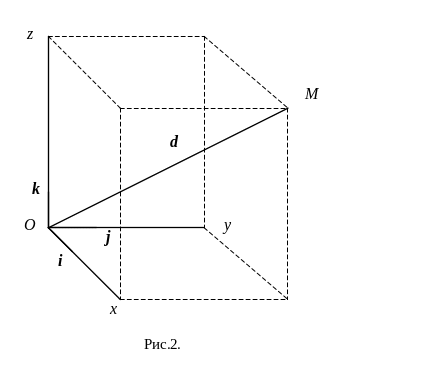
Координаты вектора в прямоугольном базисе совпадают с проекциями вектора на базисные орты соответственно (рис.2), а длина вектора равна

3. Декартова система координат

Говорят, что в трехмерном пространстве введена декартова прямоугольная система координат (рис.2), если заданы:

1. некоторая точка 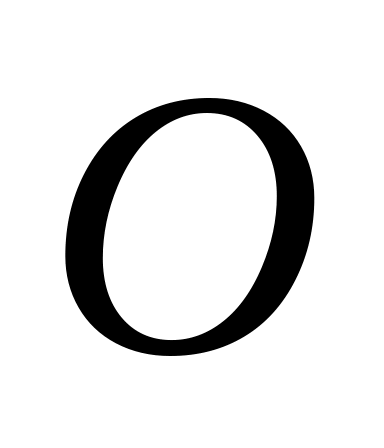, называемая началом координат;

2. прямоугольный базис 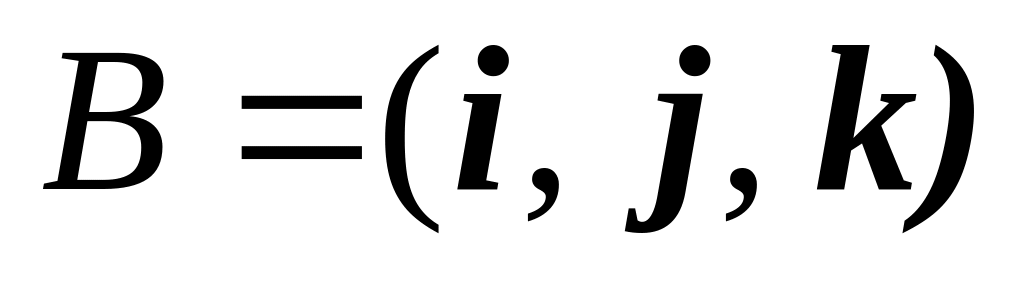на множестве всех геометрических векторов.

Оси , проведенные через точку в направлении базисных ортов , называются координатными осями системы координат .

Если M – произвольная точка пространства, то направленный отрезок называется радиус-вектором точки M, а координаты этого вектора в базисе B – координатами точки M.

Если и две произвольные точки пространства, то координаты вектора равны

,

расстояние между точками выражается формулой:

,

а середина отрезка имеет координаты:

.

Задачи.

2.1. В треугольнике ABC: , точка M – середина стороны BC. Выразить вектор через векторы a и b.

2.2. – медианы треугольника ABC. Доказать равенство .

2.3. – медианы треугольника ABC. Выразить через векторы и .

2.4. Доказать, что средняя линия треугольника параллельна его основанию и длина ее равна половине длины основания.

2.5. Доказать, что сумма векторов, соединяющих центр правильного треугольника с его вершинами, равна нулю.

2.6. Даны векторы a и b, угол между которыми 120^о. Построить вектор и определить его модуль, если .

2.7. На плоскости заданы векторы и . Убедиться, что – базис на множестве всех векторов на плоскости. Найти разложение вектора a по базису B.

2.8. Показать, что тройка векторов , образует базис на множестве всех векторов пространства. Вычислить координаты вектора в базисе и написать соответствующее разложе­ние по базису.

2.9. Найти вектор x, коллинеарный вектору и имеющий длину .

2.10. Могут ли векторы и быть сторонами треугольника?

2.11. Коллинеарны ли векторы a и b, если коллинеарны векторы и ?

2.12. При каких значениях  и  векторы и коллинеарны?

2.13. Вычислить расстояние между точками и и расстояние от точки до начала координат.

2.14. Вычислить периметр треугольника с вершинами в точках .

2.15. Показать, что треугольник ABC с вершинами – прямоугольный.

2.16. Даны три вершины параллелограмма ABCD. Найти его четвертую вершину D, противоположную B.

2.17. Даны две смежные вершины параллелограмма и точка пересечения его диагоналей . Найти две другие вершины.

2.18. На оси абсцисс найти точку M, расстояние от которой до точки равно 5.

2.19. На оси ординат найти точку M, равноудаленную от точек

и .