6. Понятие функции
Пусть
X
и
Y
числовые
множества и пусть каждому элементу х
из множества Х
ставится
в соответствие по какому-то закону f
один элемент у
из множества Y.
Тогда говорят, что определена функциональная
зависимость у
от
х
по закону
.
Независимая переменная х
называется
аргументом, а зависимая переменная у
– значением функции. Множество Х
– это область определения функции
,
а Y
– область значений. Совокупность точек
координатной плоскости хОу,
удовлетворяющих уравнению
,
называется графиком этой функции.
7. Предел функции
Пусть
функция
определена в некоторой окрестности
точки
,
за исключением, быть может, самой точки
.
Число
А
называется
пределом
функции
в точке
,
записывается
,
если для любого, сколь угодно малого,
существует число
такое, что для всех
,
удовлетворяющих неравенству
,
выполняется неравенство
.
На -языке это определение можно записать следующим образом:
.
Выражение
«предел функции в точке
»
часто заменяют выражением «предел
функции при х,
стремящемся к
,
или, предел функции при
».
Рассматривают
также односторонние
пределы
функции: предел слева
(х
стремится к
,
оставаясь меньше
;
)
и предел справа
(х
стремится к
,
оставаясь больше
;
).
Если односторонние пределы равны:
,
то предел функции
в точке
существует и равен А.
Если односторонние пределы различны,
или хотя бы один из них не существует,
то не существует и предела функции в
соответствующей точке.
Теоремы о пределах функции
Если предел функции при существует, то он единственен.
Если функция при имеет предел, то существует окрестность точки , на которой функция ограничена.
Если функция функции тождественно равна постоянной С, то
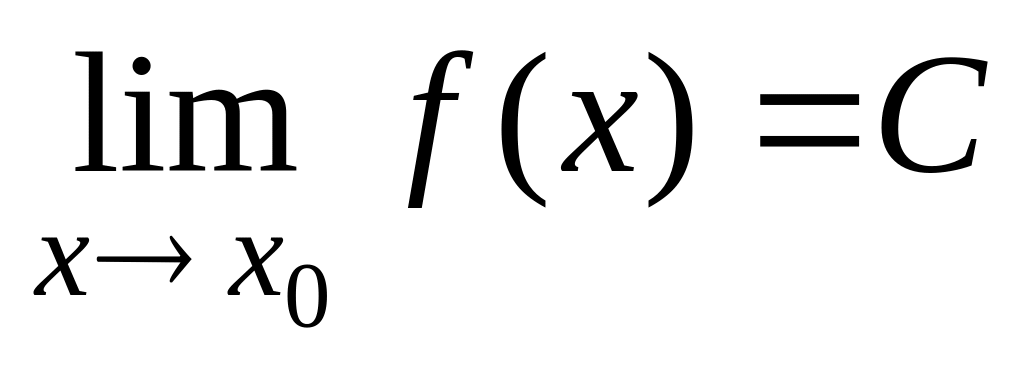.Пусть при существуют пределы функций 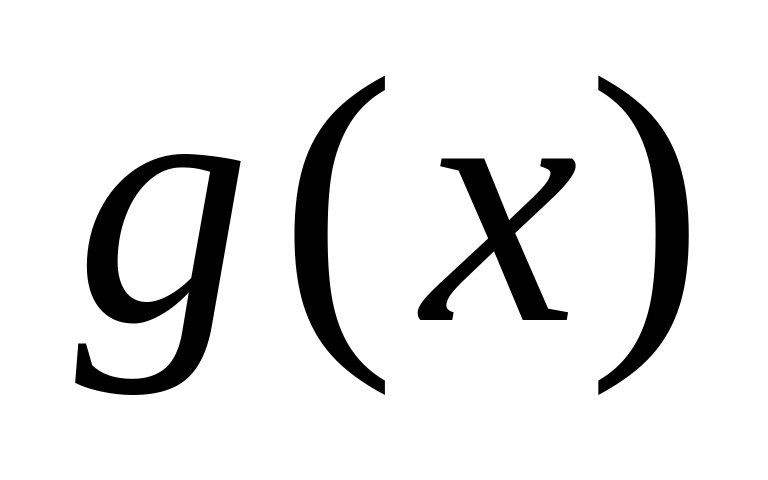и
(
и
).
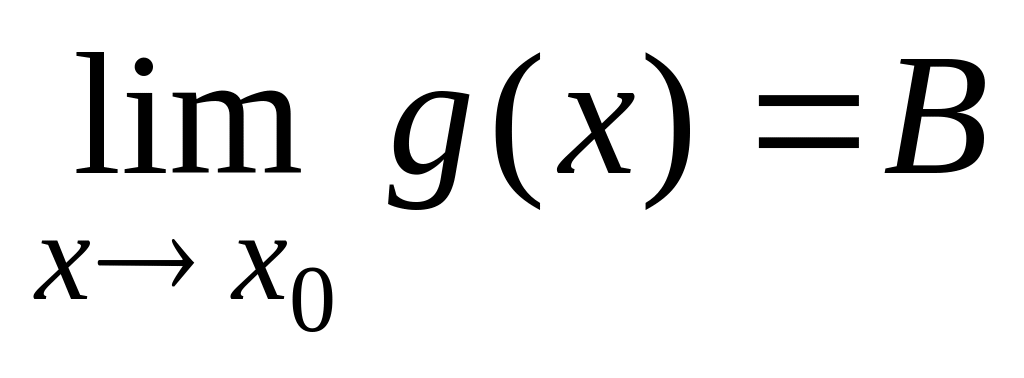Тогда при
существуют также пределы суммы, разности
и произведения этих функций, при этом:
а)
;
б)
;
в)
если, кроме того,
,
то существует предел частного
и
.
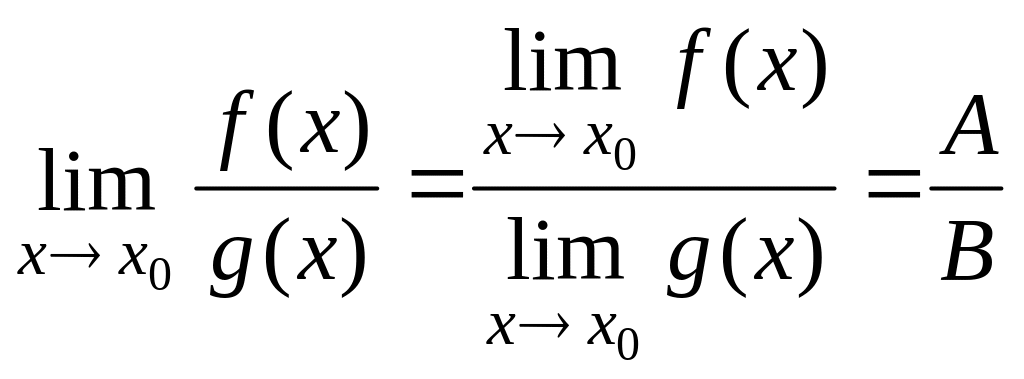Если
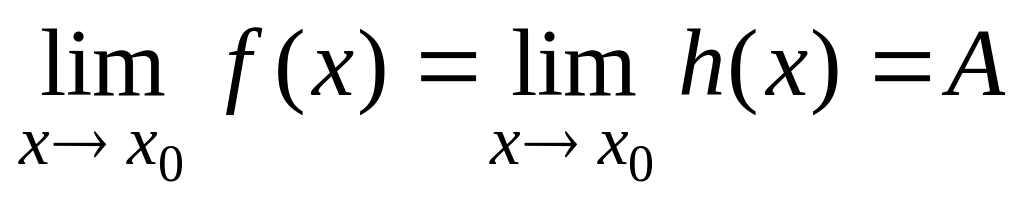и существует окрестность точки
,
что для каждого х
из этой окрестности, за исключением,
быть может, самой точки
,
справедливо неравенство
,
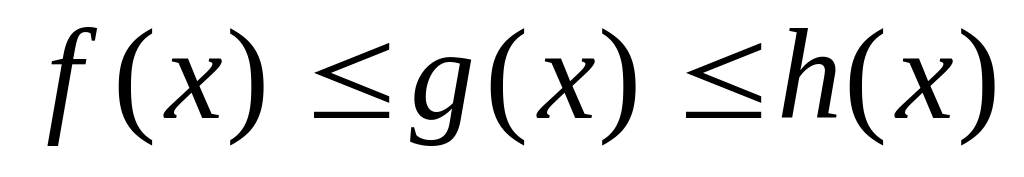то существует предел функции
,
причем
.
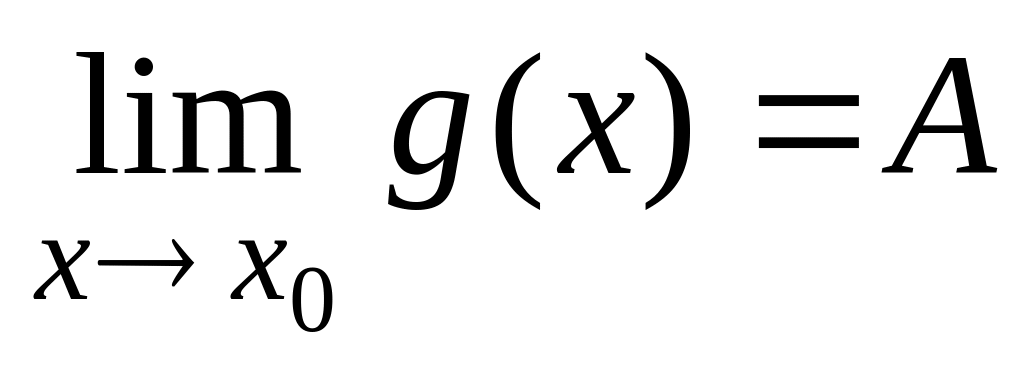При вычислении пределов алгебраических выражений, когда переменная стремится к конечному числу , надо сначала подставить это число в выражение. Если значение выражения вычисляется, то полученное число и является его пределом. Если вычисления невозможны, т.е. выражение представляет собой неопределенность, то ее надо раскрыть, используя формулы преобразования выражений.
При вычислении пределов функций, содержащих иррациональные выражения, применяются методы избавления от иррациональности: умножение числителя и знаменателя дроби на сопряженное выражение, введение новой переменной или применение формул сокращенного умножения.
Пример.
Вычислить пределы:
а)
;
б)
;
в)
.
Решение.
а) Применяя формулы 4.а и 4.б, получаем
.
б)
При
числитель и знаменатель дроби равны
нулю, имеем неопределенность типа
.
Чтобы раскрыть ее, разложим многочлены
на множители:
.
в)
При
числитель и знаменатель дроби равны
нулю, имеем неопределенность типа
.
Чтобы раскрыть эту неопределенность,
предварительно преобразуем дробь
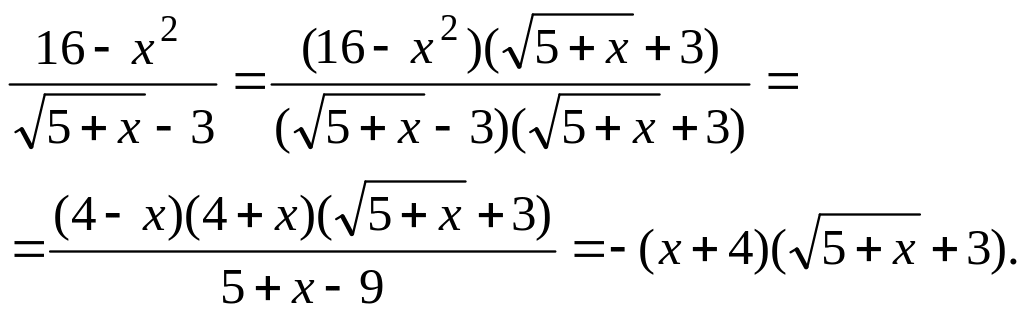
Переходя к пределу, получаем
.